[数据结构与算法]110 平衡二叉树

题目

给定一个二叉树，判断它是否是高度平衡的二叉树。

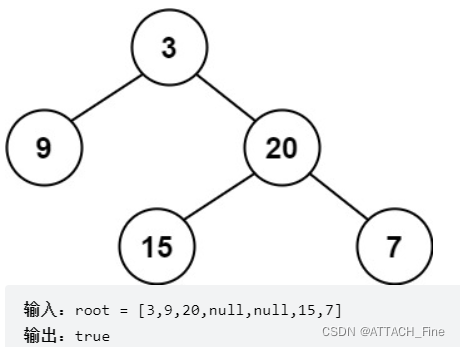
本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

递归三部曲

（1）确定递归函数的参数和返回值：
确定哪些参数是递归的过程中需要处理的
明确每次递归的返回值是什么进而确定递归函数的返回类型。
这个题目中：
递归的参数就是树的每个节点
返回值就是当前这个节点所在的高度
（2）确定终止条件：
递归算法, 运行的时候，经常会遇到栈溢出的错误，就是没写终止条件或者终止条件写的不对，操作系统也是用一个栈 的结构来保存每一层递归的信息，如果递归没有终止，操作系统的内存栈必然就会溢出。

这个题目中，终止条件是节点为空的时候，
（3）确定单层递归的逻辑：
确定每一层递归需要处理的信息。

这个题目中，单层递归的逻辑就是先判断当前节点的左右子树是否是平衡二叉树。
如果不是平衡二叉树，返回-1表明整个二叉树不是平衡二叉树
如果当前节点的左右子树是平衡二叉树，使用当前子树的左右子树高度来判断当前节点是否是平衡二叉树。如果不是，返回-1；如果是平衡二叉树，返回当前节点的高度给上一层节点。

思路

1、判断左了树或右子树是否返回-1
2、如果左子树已经返回-1, 就不需要再递归右子树了
3、如果当前节点的左右子树高度差超过1, 返回-1

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isBalanced(TreeNode root) {
        return Height(root) != -1 ? true : false;

    }

    public int Height(TreeNode root){
        if(root == null){
            return 0;
        }

        int LeftHeight;
        int RightHeight;

        if((LeftHeight = Height(root.left))==-1 || (RightHeight = Height(root.right))==-1 || Math.abs(LeftHeight-RightHeight) > 1){
            return -1;
        }
        return Math.max(LeftHeight,RightHeight)+1;
    }
}