[数据结构与算法]第十一届蓝桥杯 —— 第 H 题 子串分值和

题目

?

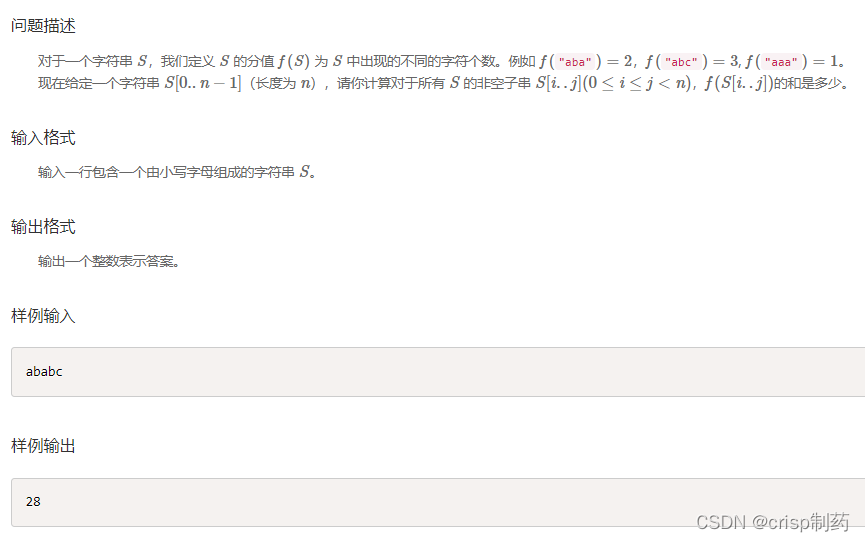
?参考博客：第十一届蓝桥杯 ——子串分值和_六级不考550+不改名-CSDN博客_蓝桥杯各题分值

解法：乘法原理，O（n）

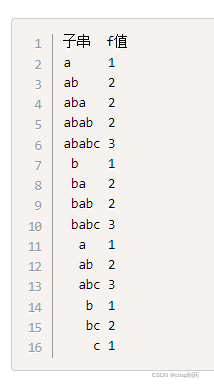
我们可以直接认为对于每一个字符串，只有第一次在这个字符串中出现的字母对它所能形成的无重复字符串有贡献，例如对于”aba”，那么它所能行成的无重复字符串为”ab”，则我们就认为只是第一次出现的aa和第一次出现的bb对这个无重复字符串有贡献。

一个字符只有第一次出现时是有贡献的，记录每一个字符上次在字符串中出现的位置，以此判断当前字符距离上一次出现中间多少字符，计算该字符作为第一次出现的子串数，它对这些子串都是有贡献的（即作为不同的字符出现）。

接下来就是统计，以某个字符为第一次出现的字母的字串数量了，

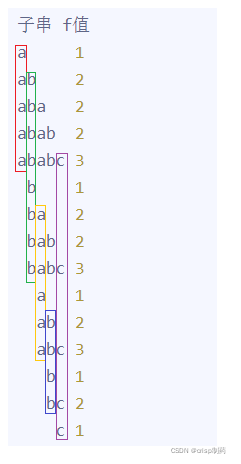
枚举每一个字母，统计它所能贡献的无重复字符串的数量。定义last[i]表示字符i在当前枚举点之前最后一次出现的位置，显然这个字母所能贡献的无重复字符串的左端点可以出现在[last[i]+1,i]，右端点就在[i,n]之中，因此这样我们就是就能做到当前(类)字母只作用没有被当前(类)字母作用过的串，当前字母作用不到以它后面任意字母开头的所有子串，所以左端的总和为 i-last[i]? , 右端的总和为? n-i+1? 因此数量就是:? ? (i?last[i])?(n?i+1)

#include <iostream>
#include <cstring>
using namespace std;

typedef long long LL;
const int N = 1e5 + 10;
char str[N];
int last[30];

int main() {
    scanf("%s", str + 1);
    int n = strlen(str + 1);
    LL res = 0;
    for (int i = 1; i <= n; i++) {
        res += 1ll * (i - last[str[i] - 'a']) * (n - i + 1);
        last[str[i] - 'a'] = i;//更新枚举的点
    }
    printf("%lld\n", res);
    return 0;
}

?