线性表是什么？

全名为线性存储结构，线性表是最基本、最简单、也是最常用的一种数据结构。线性表（linear list）是数据结构的一种，一个线性表是n个具有相同特性的数据元素的有限序列。
线性表中数据元素之间的关系是一对一的关系，即除了第一个和最后一个数据元素之外，其它数据元素都是首尾相接的（注意，这句话只适用大部分线性表，而不是全部。比如，循环链表逻辑层次上也是一种线性表（存储层次上属于链式存储，但是把最后一个数据元素的尾指针指向了首位结点）。
使用线性表存储的数据，如同向数组中存储数据那样，要求数据类型必须一致，也就是说，线性表存储的数据，要么全部都是整形，要么全部都是字符串。一半是整形，另一半是字符串的一组数据无法使用线性表存储。

特性

1．集合中必存在唯一的一个“第一元素”。
2．集合中必存在唯一的一个 “最后元素” 。
3．除最后一个元素之外，均有唯一的后继(后件)。
4．除第一个元素之外，均有唯一的前驱(前件)。

顺序存储结构和链式存储结构的区别

在这里插入图片描述
如图 3a) 所示，将数据依次存储在连续的整块物理空间中，这种存储结构称为顺序存储结构（简称顺序表）；
如图 3b) 所示，数据分散的存储在物理空间中，通过一根线保存着它们之间的逻辑关系，这种存储结构称为链式存储结构（简称链表）；

顺序存储结构（线性表）

是线性表的一种，同样是用于存储逻辑关系“一对一”的数据。顺序表对数据的物理存储结构也有要求。顺序表存储数据时，会提前申请一整块足够大小的物理空间，然后将数据依次存储起来，存储时做到数据元素之间不留一丝缝隙。
例如，使用顺序表存储集合 {1,2,3,4,5}，数据最终的存储状态如图所示：
在这里插入图片描述
通过观察图 1 中数据的存储状态，我们可以发现，顺序表存储数据同数组非常接近。其实，顺序表存储数据使用的就是数组。

链式存储结构（链表）

单向链表

与顺序表不同，链表不限制数据的物理存储状态，换句话说，使用链表存储的数据元素，其物理存储位置是随机的。
例如，使用链表存储 {1,2,3}，数据的物理存储状态如图所示：
在这里插入图片描述
以上图片根本无法体现出各数据之间的逻辑关系。对此，链表的解决方案是，每个数据元素在存储时都配备一个指针，用于指向自己的直接后继元素。如图所示：

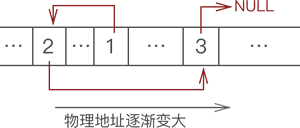
综上：数据元素随机存储，并通过指针表示数据之间逻辑关系的存储结构就是链式存储结构。

链表的节点

链表中每个数据的存储都由以下两部分组成：

数据元素本身，其所在的区域称为数据域；
指向直接后继元素的指针，所在的区域称为指针域；
节点结构：

链表实际存储的是一个一个的节点，真正的数据元素包含在这些节点中，如图：
在这里插入图片描述

头节点，头指针和首元节点

其实，图 4 所示的链表结构并不完整。一个完整的链表需要由以下几部分构成：
头指针：
一个普通的指针，它的特点是永远指向链表第一个节点的位置。很明显，头指针用于指明链表的位置，便于后期找到链表并使用表中的数据；
节点：
链表中的节点又细分为头节点、首元节点和其他节点：
头节点：
其实就是一个不存任何数据的空节点，通常作为链表的第一个节点。对于链表来说，头节点不是必须的，它的作用只是为了方便解决某些实际问题；
首元节点：
由于头节点（也就是空节点）的缘故，链表中称第一个存有数据的节点为首元节点。首元节点只是对链表中第一个存有数据节点的一个称谓，没有实际意义；
其他节点：链表中其他的节点；
因此，一个存储 {1,2,3} 的完整链表结构如图
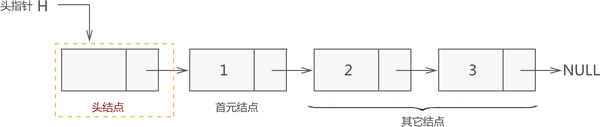
在这里插入图片描述
注意：链表中有头节点时，头指针指向头节点；反之，若链表中没有头节点，则头指针指向首元节点

双向链表

双向链表其实是单链表的改进。
当我们对单链表进行操作时，有时你要对某个结点的直接前驱进行操作时，又必须从表头开始查找。这是由单链表结点的结构所限制的。因为单链表每个结点只有一个存储直接后继结点地址的链域，那么能不能定义一个既有存储直接后继结点地址的链域，又有存储直接前驱结点地址的链域的这样一个双链域结点结构呢？这就是双向链表。
在双向链表中，结点除含有数据域外，还有两个链域，一个存储直接后继结点地址，一般称之为右链域；一个存储直接前驱结点地址，一般称之为左链域。
单向链表：
在这里插入图片描述
双向链表：