二叉树的概念
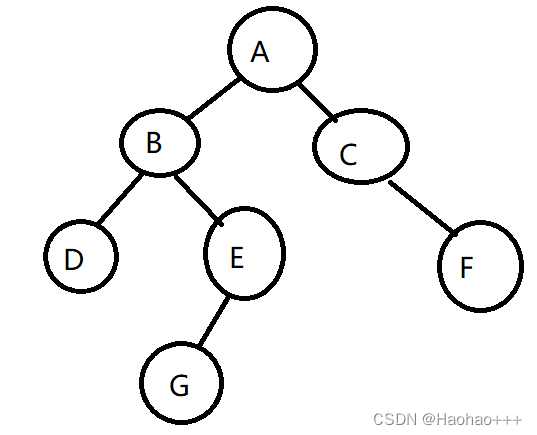
二叉树是指度不超过2的树,可以由n个结点构成,如下图。
二叉树的创建
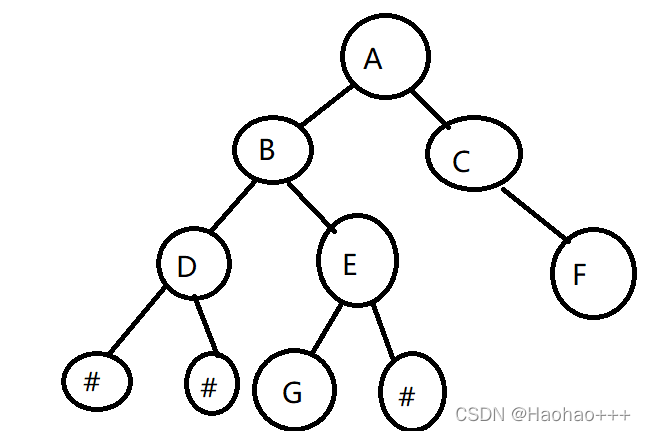
注意:输入的格式,如下图,D结点的孩子结点,空结点用#代替,直到最后一层就可以停止输入,以下面这棵树为例,则我们的输入为 ABCDE#F##G#####
class BiTreeNode:
def __init__(self, data):
self.data = data
self.lchild = None
self.rchild = None
class CreateBiTree:
"""
str_tree: 传入字符串
return: 返回根结点
"""
def __init__(self, str_tree):
self.str_tree = str_tree
def create_tree(self):
l1 = list(self.str_tree)
l1 = [None if i == '#' else i for i in l1] # 将#转为None
nodes = [BiTreeNode(l1[i]) for i in range(len(l1))] # 初始化各个结点
root = nodes[0]
for i in range(len(l1)):
if 2*i+2 > len(l1): # 循环到最后的右孩子结束
break
cur_node = nodes[i]
if nodes[2*i+1].data:
cur_node.lchild = nodes[2*i+1] # 当前结点的左孩子
if nodes[2*i+2].data:
cur_node.rchild = nodes[2*i+2] # 当前结点的右孩子
return root
def __call__(self):
return self.create_tree()
a = CreateBiTree('ABCDE#F##G#####')
root = a() # 调用__call__方法
print('根结点为:', root.data)
二叉树的遍历
前序遍历
前序遍历指先访问根结点,再访问该结点的左孩子和右孩子。继续以这棵树为例。
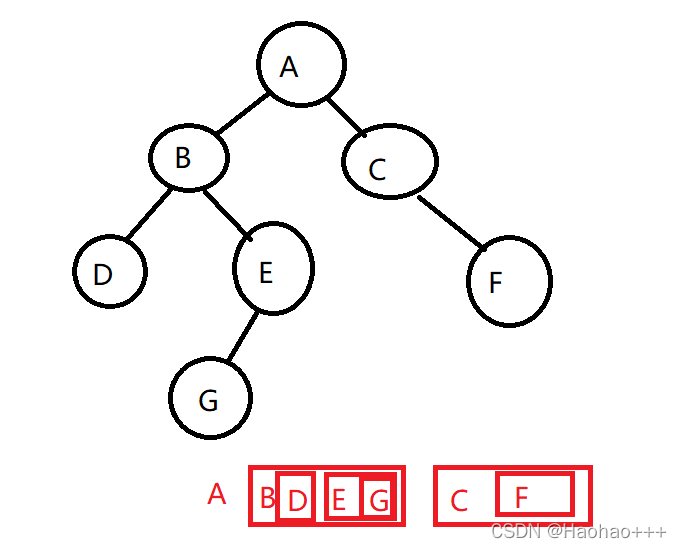
第一步,访问根结点A,然后是B、D、E、G这棵左子树和C、F右子树。
第二步,访问B、D、E、G子树的根结点B,然后是D这棵左子树和E、G这棵右子树。
第三步,访问D左子树根结点。没有子树则无需访问。
第四步,访问E、G这棵右子树的根结点E,然后是左子树G。
第五步,访问左子树G的根结点G。
第六部,访问C、F右子树的根结点C,然后是F右子树。
第七步,访问F右子树的根结点F。
def pre_order(root):
# 前序排列
if root:
print(root.data, end=',')
pre_order(root.lchild)
pre_order(root.rchild)
中序遍历
中序排列是先访问左子树,再访问根结点,然后是右子树。以上个树为例。
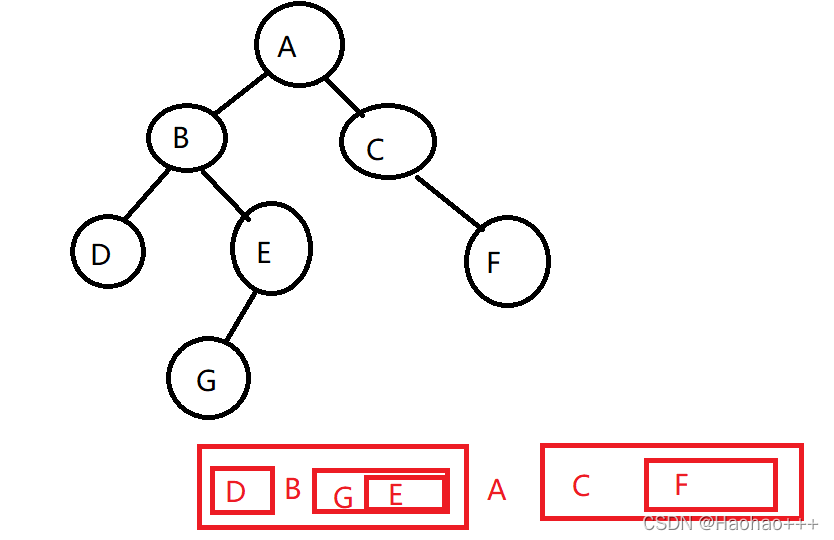
第一步,因为B、D、E、G一定在A的左边,C、F一定在A的左边,所以可以先把A写在中间。
第二步,分析左子树,同理可得,先把B写在中间,因为只有D是B的左子树,那么D肯定在B的左边,以此类推…
def in_order(root):
# 中序排列
if root:
in_order(root.lchild)
print(root.data, end=',')
in_order(root.rchild)
后序遍历
后序遍历则是先访问左子树和右子树,再访问根结点。以上棵树为例。
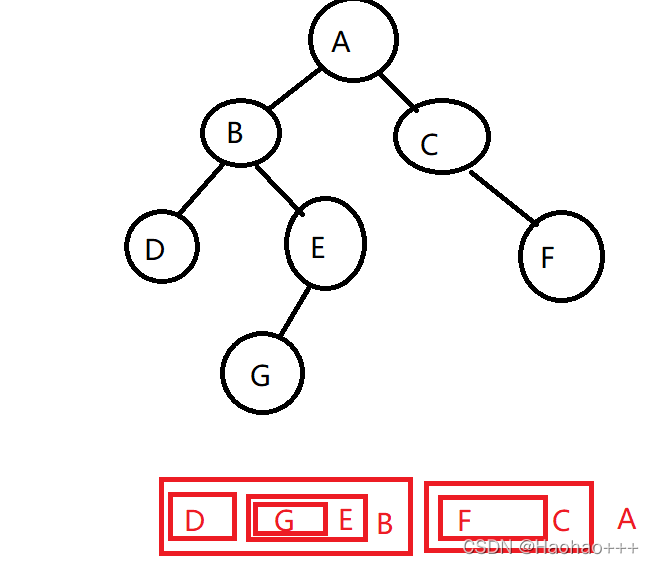
第一步,因为根结点最后访问,所以可以先把A写在最后,然后在访问左子树和右子树。
第二步,访问,D、G、E、B这棵左子树,同理可得,可以先把B写在最后,然后在访问左子树和右子树,以此类推…
def post_order(root):
# 后序排列
if root:
post_order(root.lchild)
post_order(root.rchild)
print(root.data, end=',')
层次遍历
层次遍历是一层一层遍历,从左到右,从上到下,以上棵树为例。
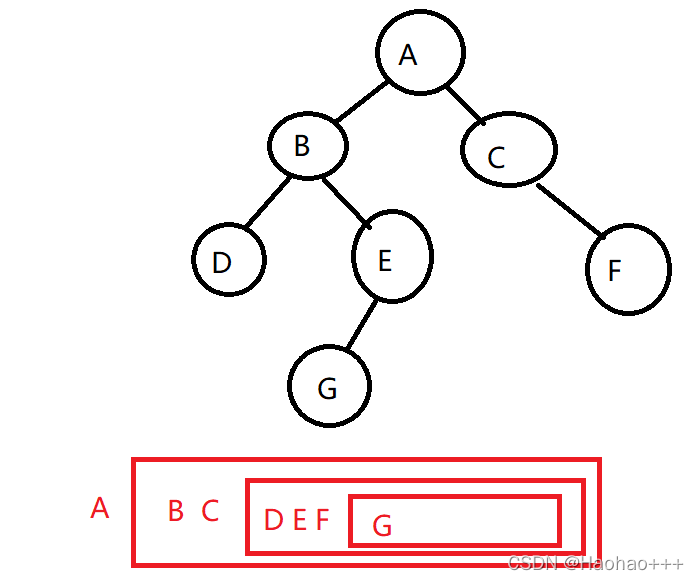
逐层遍历。
from collections import deque
def level_order(root):
# 层序排列
queue = deque()
queue.append(root)
while len(queue) > 0:
node = queue.popleft()
print(node.data, end=',')
if node.lchild:
queue.append(node.lchild)
if node.rchild:
queue.append(node.rchild)
总代码
from collections import deque
class BiTreeNode:
def __init__(self, data):
self.data = data
self.lchild = None
self.rchild = None
# ABCDE#F##G#####
class CreateBiTree:
"""
str_tree: 传入字符串
return: 返回根结点
"""
def __init__(self, str_tree):
self.str_tree = str_tree
def create_tree(self):
l1 = list(self.str_tree)
l1 = [None if i == '#' else i for i in l1]
nodes = [BiTreeNode(l1[i]) for i in range(len(l1))]
root = nodes[0]
for i in range(len(l1)):
if 2*i+2 > len(l1):
break
cur_node = nodes[i]
if nodes[2*i+1].data:
cur_node.lchild = nodes[2*i+1]
if nodes[2*i+2].data:
cur_node.rchild = nodes[2*i+2]
return root
def __call__(self):
return self.create_tree()
class BiTreeSorted:
def __init__(self, root):
self.root = root
def pre_order(self, root):
# 前序排列
if root:
print(root.data, end=',')
self.pre_order(root.lchild)
self.pre_order(root.rchild)
def in_order(self, root):
# 中序排列
if root:
self.in_order(root.lchild)
print(root.data, end=',')
self.in_order(root.rchild)
def post_order(self, root):
# 后序排列
if root:
self.post_order(root.lchild)
self.post_order(root.rchild)
print(root.data, end=',')
def level_order(self, root):
# 层序排列
queue = deque()
queue.append(root)
while len(queue) > 0:
node = queue.popleft()
print(node.data, end=',')
if node.lchild:
queue.append(node.lchild)
if node.rchild:
queue.append(node.rchild)
def __call__(self):
print('前序排列')
self.pre_order(self.root)
print()
print('中序排列')
self.in_order(self.root)
print()
print('后序遍历')
self.post_order(self.root)
print()
print('层序遍历')
self.level_order(self.root)
print()
a = CreateBiTree('ABCDE#F##G#####')
root = a()
print('根结点为:', root.data)
sorted = BiTreeSorted(root)
sorted() # 调用__call__方法
结果为:
