有向无环图:无环的有向图,简称DAG图(Directed Acycline Graph)

有向无环图常用来描述一个工程或系统的进行过程。(通常吧计划、施工、生产、程序流程等当成是一个工程)
一个工程可以分为若干个 子工程,只要完成了这些子工程(活动),就可以导致整个工程的完成
AOE网:关键路径
- 用一个有向图表示一个工程的各子工程及其相互制约的关系,以弧表示活动,以顶点表示活动的开始或结束事件,称这种有向图为边表示活动的网,简称为AOE网(Activity On Edge)
- 把工程计划表示为边表示活动的网络,即AOE网,用顶点表示事件,弧表示活动,弧的权表示活动持续时间。事件表示在它之前的活动已经完成,在它之后的活动可以开始
- 例:准备一个小型家庭宴会,晚6点开始最迟几点开始准备?压缩哪项活动时间可以使总时间减少?
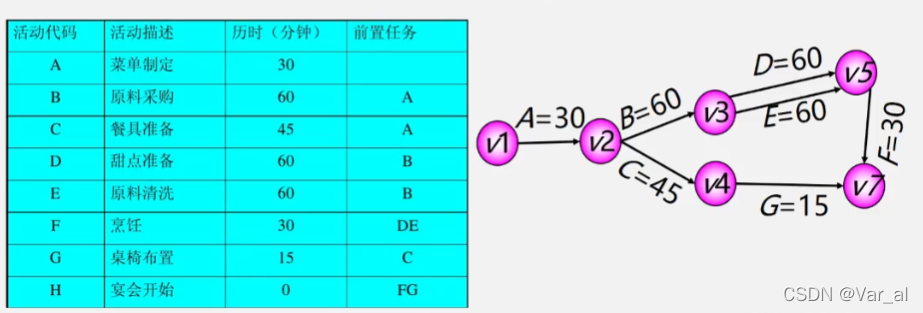
事件v1————表示整个工程开始(源点:入度为0的顶点)
事件v7————表示整个工程结束(汇点:出度为0的顶点)
对于AOE网,我们关心连个问题:
- 完成整项工程至少需要多少时间?
- 哪些活动是影响工程进度的关键
关键路径——路径长度最长的路径
路径长度——路径上各活动持续时间之和
确定关键路径,需要定义4个描述量:
ve(vj)——表示事件vj的最早发生时间
例:ve(v1) = 0 ve(v2) = 30
vl(vj)——表示事件vj的最迟发生时间
例:ve(v4) = 165
e(i)——表示活动ai的最早开始时间
例:e(a3) = 30
l(i)———表示活动ai的最迟开始时间
例:l(a3) = 120
l(i) - e(i)——表示完成活动ai的时间余量。例:l(3) - e(3) = 90
关键活动——关键路径上的活动,即l(i)-e(i)==0的活动
如何找l(i)-e(i)==0的关键活动?
设活动ai用弧<j, k>表示,其持续时间记为:Wj,k
则有:
(1) e(i) = ve(j)
(2) l(u) = vl(k)-Wj,k
如何求ve(j)和vl(j)?
(1)从ve(1)=0开始向前递推,ve(j) = Max{ve(i) + Wi,j}, <i,j>∈T, 2 ≤ j ≤ n,其中T是所有以j为头的弧的集合。
(2)从vl(i)=Min{vl(j) - Wi,j}, <i,j> ∈ S,1 ≤ i ≤ n-1,其中S是所有以i为尾的弧的集合。