1.1)什么是图结构
图中的一个一个的点称为顶点;这一条一条的线,代表着顶点之间的关系,我们将其称之为边。
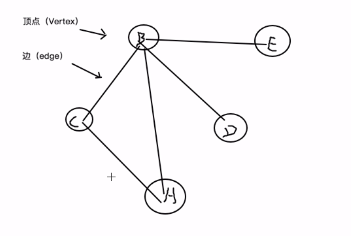
如果两个顶点之间可以通过一条边进行连通,那么就将这两个点称为是邻接的,反之就不是邻接的。比如说B和C、B和A这些顶点之间就是邻接的,而A和D就不是邻接的。
有向图和无向图指的就是边是否是有方向的。如图所示:
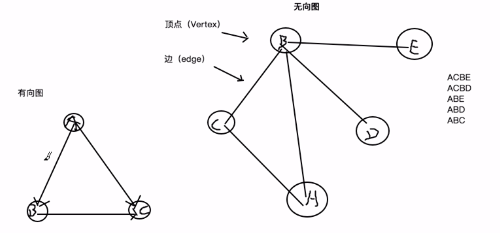
带权图指的就是,我们可以给图中的边,给它标识上一个有意义的数据值,比如说是A城市(顶点)到B城市(顶点)所需要的时间,等等,这就是带权图。
1.2)图的数据如何存储:
要实现图这种数据结构,首先就是要思考图是如何去存储数据的,是使用链表进行存储,还是使用数组进行存储呢?
使用链表是不行的,因为我们将图中的每个顶点都是链表中的一个节点,那么图中的每个节点都可能连接有多个其他的顶点,这个时候这个连接关系我们如何使用链表来进行表示?在链表中即使是双向链表也只是指向了上一个下一个节点,无法指向其他的节点。所以说如果用链表来存储数据的话,指针的部分就不太好写。
图结构我们都是这样设计的:
首先,我们定义一个数组,将图中的顶点都放入这个数组中。
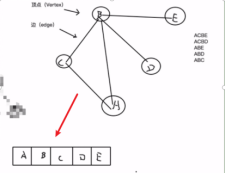
然后我们再单独找一个地方来单独存放顶点与顶点之间的关系。比如说A顶点和B顶点之间有没有边,A顶点和D顶点之间有没有边,这些。
存放的方式有两种,一种是邻接表,一种是邻接矩阵。
邻接表示例:
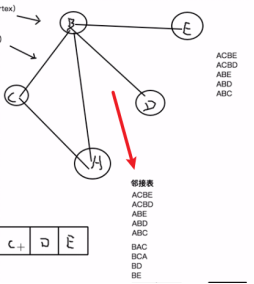
将每个节点从该节点出发可以到达的所有的顶点的路径都一一列举出来。
邻接矩阵示例:

将每个节点与其他的节点依次进行判断,是邻接的顶点,则标记为1,不是邻接的顶点则标记为0。
1.3)图的遍历:
图的遍历分为①深度优先搜索算法和②广度优先搜索算法,两种方式。

举例说明:

对于这样一个图。
深度优先遍历的方式为:先从A节点出发,到B节点,再接着从B节点出发,到达C节点,再接着从C节点出发,到达C的下一个节点,发现没有了,则退回到C的上一个节点B节点,从B节点到D节点,再接着到D节点的下一个节点,发现D没有下一个节点了,则退回到D节点的上一个节点B节点,再到B节点的下一个未被遍历过的节点E节点,再接着到达E节点的下一个节点,发现E节点没有了,于是退回到E节点的上一个节点B节点,B节点下边的节点也没有了,于是退回到B节点的上一个节点A节点,然后遍历A节点的下一个节点C节点,再之后A节点的下一个节点也遍历完了,于是整个图遍历完成。
广度优先遍历的方式为:先从A节点出发,到下一级节点B节点,然后退回到A节点,再遍历A节点的未被遍历的下一级节点C节点,A节点的下一级的所有节点被遍历完成之后,再开始从下一级节点比如说是B节点开始,遍历B节点的下一级的所有节点。最终完成图的遍历。
深度优先遍历和广度优先遍历的区别:
①,深度优先遍历是一直先遍历某一个节点的下一个节点,直到没有了下一个节点,再退回到上一级节点,最终遍历完成。
②,广度优先遍历是先遍历完第一个节点的下一级的所有节点,然后再依次遍历完成下下一级的所有节点,是一级一级的完成遍历。
③,深度优先遍历相当于是由线到面,广度优先遍历相当于是由面到线。
给每个节点设置一个是否已访问的标识:
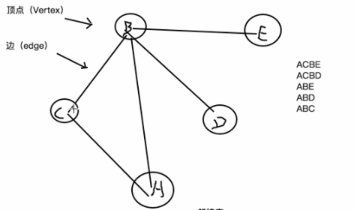
如图所示:
- 比如说DFS深度优先遍历,从A节点到B节点,再从B节点到C节点,走不通了,退回上一级,到B节点,此时B节点有三个选择,到C节点、到D节点、到E节点,而C节点刚才已经访问过了,如果证明某个节点已经访问过了呢?所以我们应该给每个节点设置一个标识,标识是否已经访问过,如果已经访问过了,则不再进行第二次访问。BFS广度优先遍历同样如此。
1.4)DFS深度优先遍历
使用辅助栈:
| 递归就是隐式的栈。 |
如上图所示,比如说DFS深度优先遍历,从A节点到B节点,再从B节点到C节点,走不通了,退回上一级,到B节点。那么此时,程序是如何退回到上一级的呢?
所以此时我们的办法是使用一个栈来作为辅助数据结构:
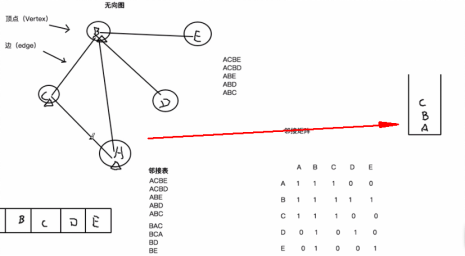
1. 首先,访问到A节点,我们将A节点标识为已访问,然后,将A节点进栈,然后根据邻接矩阵的位置,接着我们会访问B节点,将B节点标识为已访问,然后,将B节点进栈,接着,将C节点识为已访问,然后,将C节点进栈。
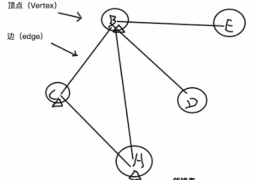

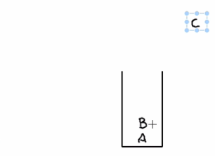
?2. 如上图所示,在邻接矩阵中,我们可以看到C节点到目前还未访问过的D节点和E节点都不通,那么这个时候就需要退回上一级了,怎么退回?
退回上一级的办法就是,我们将C节点从辅助栈中弹出去,弹出去之后此时辅助栈中的栈顶元素就是B节点了,接着我们重新从B节点开始往后找,除去已访问过的A节点和C节点之后,就到了D节点了。
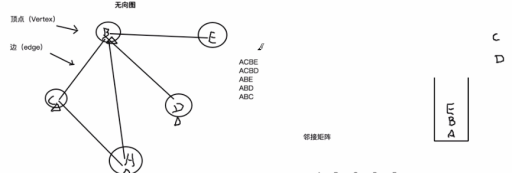
接着在邻接矩阵中发现D节点也没有下一个未被访问过的节点了,此时将D节点弹出栈,栈顶元素又回到了B节点,此时发现B节点还有下一个未被访问过的节点E,此时将E节点标识为已访问,并将E节点进栈。
接着,发现E节点没有下一个未被访问过的节点了,将E弹出栈;然后回到上一级元素-此时的新栈顶元素B,发现B节点也没有下一个未被访问过的节点了,将B弹出栈;然后发现A节点也没有下一个未被访问过的节点了,将A弹出栈;
栈为空了,DFS深度优先搜索结束。
代码演示:
public static void main(String[] args) {
??????GraphNode e = new GraphNode("E");
??????GraphNode d = new GraphNode("D");
??????GraphNode c = new GraphNode("C");
??????GraphNode b = new GraphNode("B");
??????ArrayList<GraphNode> graphNodes1 = new ArrayList<>();
??????graphNodes1.add(b);
??????graphNodes1.add(c);
??????GraphNode a = new GraphNode("A", graphNodes1);
??????ArrayList<GraphNode> graphNodes2 = new ArrayList<>();
??????graphNodes2.add(b);
??????graphNodes2.add(a);
??????c.neighbors = graphNodes2;
??????ArrayList<GraphNode> graphNodes3 = new ArrayList<>();
??????graphNodes3.add(c);
??????graphNodes3.add(a);
??????graphNodes3.add(d);
??????graphNodes3.add(e);
??????b.neighbors = graphNodes3;
??????ArrayList<GraphNode> graphNodes4 = new ArrayList<>();
??????graphNodes4.add(b);
??????ArrayList<GraphNode> graphNodes5 = new ArrayList<>();
??????graphNodes5.add(b);
??????d.neighbors = graphNodes4;
??????e.neighbors = graphNodes4;
??????List<GraphNode> dfs = dfs(a);
??????List<String> dfsStr = dfs.stream().map(e2 -> e2.valStr).collect(Collectors.toList());
??????System.out.println("JSONObject.toJSON(dfs) = " + JSONObject.toJSON(dfsStr));
}
/**
?* DFS深度优先遍历
?*/
public static List<GraphNode> dfs(GraphNode firstNode) {
??????//判断是否已访问过的Set:里边存放的都是已经访问过的元素;
??????Set<GraphNode> isVisit = new LinkedHashSet<>();
??????//新建一个辅助栈:
??????Deque<GraphNode> stack = new LinkedList<>();
??????//开始DFS:
??????//首先,从A节点开始访问:
??????isVisit.add(firstNode);
??????//然后,将A节点进栈:
??????stack.push(firstNode);
??????//查看A节点的邻接节点:
??????out:
??????while (!stack.isEmpty()) {
????????????//此时的栈顶元素:
????????????GraphNode zhanDingEle = stack.peek();
????????????//找出该栈顶元素的所有邻接节点:
????????????List<GraphNode> neighborList = zhanDingEle.neighbors;
????????????if (neighborList != null && neighborList.size() > 0) {
??????????????????for (GraphNode neighborNode : neighborList) {
????????????????????????//如果该邻接节点已经被访问过,则直接continue:
????????????????????????if (isVisit.contains(neighborNode)) {
??????????????????????????????continue;
????????????????????????}
????????????????????????//如果没有被访问过,则将该元素进栈,并标识为已访问,然后继续进行找新栈顶元素的邻接节点;
????????????????????????else {
??????????????????????????????stack.push(neighborNode);
??????????????????????????????isVisit.add(neighborNode);
??????????????????????????????continue out;
????????????????????????}
??????????????????}
????????????}
????????????//如果该元素的所有邻接节点都被访问过了:则返回上一级,即—将该栈顶元素出栈,使用新的栈顶元素:
????????????stack.pop();
??????}
??????//当栈为空了,则DFS结束;
??????//返回结果;
??????return new ArrayList<>(isVisit);
}1.5)BFS广度优先遍历
使用辅助队列:
DFS深度优先遍历用的是栈作为辅助数据结构,BFS用的是队列来作为辅助数据结构-FIFO先进先出的特点。
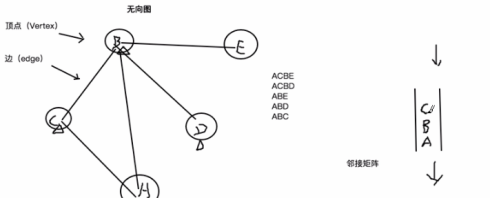
首先,访问A节点,将A节点标识为已访问,然后将A节点进队列,此时队列头是A节点,于是再访问A节点的邻接结点B节点,此时将B节点标识为已访问,然后将B节点进队列,此时队列头还是A节点,于是接着访问A节点的剩余的未访问节点,C节点,此时将C节点标识为已访问,然后将C节点进队列。
接着,A节点没有未被访问过的剩余邻接节点了,此时将队列头A节点出队列,队列头更换为B节点,于是我们再访问B节点的未被访问过的剩余邻接结点,于是D节点进队列,然后再访问B节点的未被访问过的剩余邻接结点,于是E节点进队列。
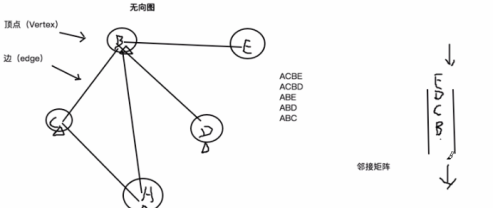
接着,B节点没有未被访问过的剩余邻接节点了,此时将队列头B节点出队列,队列头更换为C节点。
接着,C节点没有未被访问过的剩余邻接节点了,此时将队列头C节点出队列,队列头更换为D节点。
接着,D节点没有未被访问过的剩余邻接节点了,此时将队列头D节点出队列,队列头更换为E节点。
接着,E节点没有未被访问过的剩余邻接节点了,此时将队列头E节点出队列。
此时,队列为空了,BFS广度优先遍历结束。
代码演示:
public static void main(String[] args) {
??????GraphNode e = new GraphNode("E");
??????GraphNode d = new GraphNode("D");
??????GraphNode c = new GraphNode("C");
??????GraphNode b = new GraphNode("B");
??????ArrayList<GraphNode> graphNodes1 = new ArrayList<>();
??????graphNodes1.add(b);
??????graphNodes1.add(c);
??????GraphNode a = new GraphNode("A", graphNodes1);
??????ArrayList<GraphNode> graphNodes2 = new ArrayList<>();
??????graphNodes2.add(b);
??????graphNodes2.add(a);
??????c.neighbors = graphNodes2;
??????ArrayList<GraphNode> graphNodes3 = new ArrayList<>();
??????graphNodes3.add(c);
??????graphNodes3.add(a);
??????graphNodes3.add(d);
??????graphNodes3.add(e);
??????b.neighbors = graphNodes3;
??????ArrayList<GraphNode> graphNodes4 = new ArrayList<>();
??????graphNodes4.add(b);
??????ArrayList<GraphNode> graphNodes5 = new ArrayList<>();
??????graphNodes5.add(b);
??????d.neighbors = graphNodes4;
??????e.neighbors = graphNodes4;
??????List<GraphNode> dfs = bfs(a);
??????List<String> dfsStr = dfs.stream().map(e2 -> e2.valStr).collect(Collectors.toList());
??????System.out.println("广度优先遍历BFS = " + JSONObject.toJSON(dfsStr));
}
/**
?* BFS广度优先遍历
?* @param firstNode
?* @return
?*/
public static List<GraphNode> bfs(GraphNode firstNode) {
??????//1,新建一个HashSet,存储已访问过的元素;
??????Set<GraphNode> isVisit = new LinkedHashSet<>();
??????//2,新建一个队列,作为辅助数据结构:
??????Queue<GraphNode> queue = new LinkedList<>();
??????//3,先将第一个元素存入队列:
??????queue.add(firstNode);
??????isVisit.add(firstNode);
??????//4,开始循环入队列:
??????while (!queue.isEmpty()) {
????????????//队列头元素:
????????????GraphNode duilieHeadEle = queue.peek();
????????????//找该元素的所有邻接节点:
????????????List<GraphNode> neighborList = duilieHeadEle.neighbors;
????????????if (neighborList != null && neighborList.size() > 0) {
??????????????????for (GraphNode neighborNode : neighborList) {
????????????????????????//如果该节点已被访问,则直接continue;
????????????????????????if (isVisit.contains(neighborNode)) {
??????????????????????????????continue;
????????????????????????}
????????????????????????//找到了邻接节点,先将该节点设为已访问,并进入队列,然后继续找下一个邻接节点
????????????????????????isVisit.add(neighborNode);
????????????????????????queue.add(neighborNode);
????????????????????????continue;
??????????????????}
??????????????????//该节点的邻接节点遍历完之后,将该节点出队列:
??????????????????queue.poll();
????????????}
??????}
??????//当队列为空了,此时广度优先遍历完成;
??????//返回结果:
??????return new ArrayList<>(isVisit);
}