[数据结构与算法]【智能优化算法】基于曲线自适应和模拟退火的蝗虫优化算法求解单目标优化问题附matlab代码

1 简介

针对蝗虫优化算法容易陷入局部极值点,收敛速度慢,精度较差等缺点,提出曲线自适应和模拟退火蝗虫优化算法.首先,引入曲线自适应代替蝗虫优化算法关键参数的线性自适应,提高了算法的全局搜索能力;其次,在此基础上引入模拟退火算法,对蝗虫算法的劣势解具有一定概率的接收,使算法具有跳出局部最优,实现全局最优的能力.自适应缩小模拟退火中蝗虫位置随机解的范围,有利于进一步提高蝗虫算法的开发能力.通过测试函数测试,实验结果表明,改进的新算法具有更好的求解质量和收敛速度.

蝗虫的生命周期主要分为幼虫和成虫两个阶段。蝗虫在幼虫阶段群体的主要特征是行动缓慢并在小范围内移动，而在成虫阶段会有快速的跳跃性运动。这对应算法的勘探和开发两个步骤: 在勘探中，蝗虫群体跳跃性运动的行为，有利于全局搜索; 而在开发中，蝗虫群体更倾向于小范围移动，有利于局部搜索。蝗虫算法的基本思想是: 首先初始化蝗虫的位置和参数以及要迭代的次数，并计算每个蝗虫的适应度值，找出最佳的适应度值并保存相应的蝗虫( 问题的解) 到变量?T。循环更新蝗虫位置并计算每个蝗虫的适应度值，保存每次迭代最好的适应值并更新?T，迭代到最大迭代次数退出循环并返回?T( 全局最优解)?。蝗虫更新位置不考虑重力和风力的影响，位置更新由蝗虫的当前位置、目标值位置和其他蝗虫位置共同决定。其中，位置更新考虑了其他蝗虫位置，这是与粒子群算法不同的地方。粒子群通过粒子当前位置、个体最优和全局最优来更新粒子的位置，而蝗虫算法通过蝗虫当前位置、全局最优和其他蝗虫位置来更新蝗虫的位置。粒子群中其他粒子对位置的更新没有作出贡献，而蝗虫算法要求所有蝗虫都对位置的更新作出贡献。在每次迭代中都要更新参数?c，这有助于蝗虫算法避免靠近目标值太快而陷入局部最优，参数?c?也控制着蝗虫算法从勘探到开发过程的转变。当迭代到最大迭代次数时，算法结束并收敛到最优值。蝗虫算法通过提出模型和向目标更新机制使得它在未知问题的优化上可以取得很好的效果。

2 部分代码

%_________________________________________________________________________%%  Grasshopper Optimization Algorithm (GOA) source codes demo V1.0        %%                                                                         %%_________________________________________________________________________%?% The Grasshopper Optimization Algorithmfunction [TargetFitness,TargetPosition,Convergence_curve,Trajectories,fitness_history, position_history]=GOA(N, Max_iter, lb,ub, dim, fobj)?ticdisp('GOA is now estimating the global optimum for your problem....')?flag=0;if size(ub,1)==1    ub=ones(dim,1)*ub;    lb=ones(dim,1)*lb;end?if (rem(dim,2)~=0) % this algorithm should be run with a even number of variables. This line is to handle odd number of variables    dim = dim+1;    ub = [ub; 100];    lb = [lb; -100];    flag=1;end?%Initialize the population of grasshoppersGrassHopperPositions=initialization(N,dim,ub,lb);GrassHopperFitness = zeros(1,N);?fitness_history=zeros(N,Max_iter);position_history=zeros(N,Max_iter,dim);Convergence_curve=zeros(1,Max_iter);Trajectories=zeros(N,Max_iter);?cMax=1;cMin=0.00004;%Calculate the fitness of initial grasshoppers?for i=1:size(GrassHopperPositions,1)    if flag == 1        GrassHopperFitness(1,i)=fobj(GrassHopperPositions(i,1:end-1));    else        GrassHopperFitness(1,i)=fobj(GrassHopperPositions(i,:));    end    fitness_history(i,1)=GrassHopperFitness(1,i);    position_history(i,1,:)=GrassHopperPositions(i,:);    Trajectories(:,1)=GrassHopperPositions(:,1);end?[sorted_fitness,sorted_indexes]=sort(GrassHopperFitness);?% Find the best grasshopper (target) in the first population for newindex=1:N    Sorted_grasshopper(newindex,:)=GrassHopperPositions(sorted_indexes(newindex),:);end?TargetPosition=Sorted_grasshopper(1,:);TargetFitness=sorted_fitness(1);?% Main loopl=2; % Start from the second iteration since the first iteration was dedicated to calculating the fitness of antlionswhile l<Max_iter+1        c=cMax-l*((cMax-cMin)/Max_iter); % Eq. (2.8) in the paper              %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%      for i=1:size(GrassHopperPositions,1)        temp= GrassHopperPositions';       % for k=1:2:dim              S_i=zeros(dim,1);            for j=1:N                if i~=j                    Dist=distance(temp(:,j), temp(:,i)); % Calculate the distance between two grasshoppers                                        r_ij_vec=(temp(:,j)-temp(:,i))/(Dist+eps); % xj-xi/dij in Eq. (2.7)                    xj_xi=2+rem(Dist,2); % |xjd - xid| in Eq. (2.7)                                         s_ij=((ub - lb)*c/2)*S_func(xj_xi).*r_ij_vec; % The first part inside the big bracket in Eq. (2.7)                    S_i=S_i+s_ij;                end            end            S_i_total = S_i;                  %  end                X_new = c * S_i_total'+ (TargetPosition); % Eq. (2.7) in the paper              GrassHopperPositions_temp(i,:)=X_new';       end          %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%    % GrassHopperPositions    GrassHopperPositions=GrassHopperPositions_temp;        for i=1:size(GrassHopperPositions,1)        % Relocate grasshoppers that go outside the search space         Tp=GrassHopperPositions(i,:)>ub';Tm=GrassHopperPositions(i,:)<lb';GrassHopperPositions(i,:)=(GrassHopperPositions(i,:).*(~(Tp+Tm)))+ub'.*Tp+lb'.*Tm;                % Calculating the objective values for all grasshoppers        if flag == 1            GrassHopperFitness(1,i)=fobj(GrassHopperPositions(i,1:end-1));        else            GrassHopperFitness(1,i)=fobj(GrassHopperPositions(i,:));        end        fitness_history(i,l)=GrassHopperFitness(1,i);        position_history(i,l,:)=GrassHopperPositions(i,:);                Trajectories(:,l)=GrassHopperPositions(:,1);                % Update the target        if GrassHopperFitness(1,i)<TargetFitness            TargetPosition=GrassHopperPositions(i,:);            TargetFitness=GrassHopperFitness(1,i);        end    end            Convergence_curve(l)=TargetFitness;    disp(['In iteration #', num2str(l), ' , target''s objective = ', num2str(TargetFitness)])        l = l + 1;end??if (flag==1)    TargetPosition = TargetPosition(1:dim-1);end?time=toc??

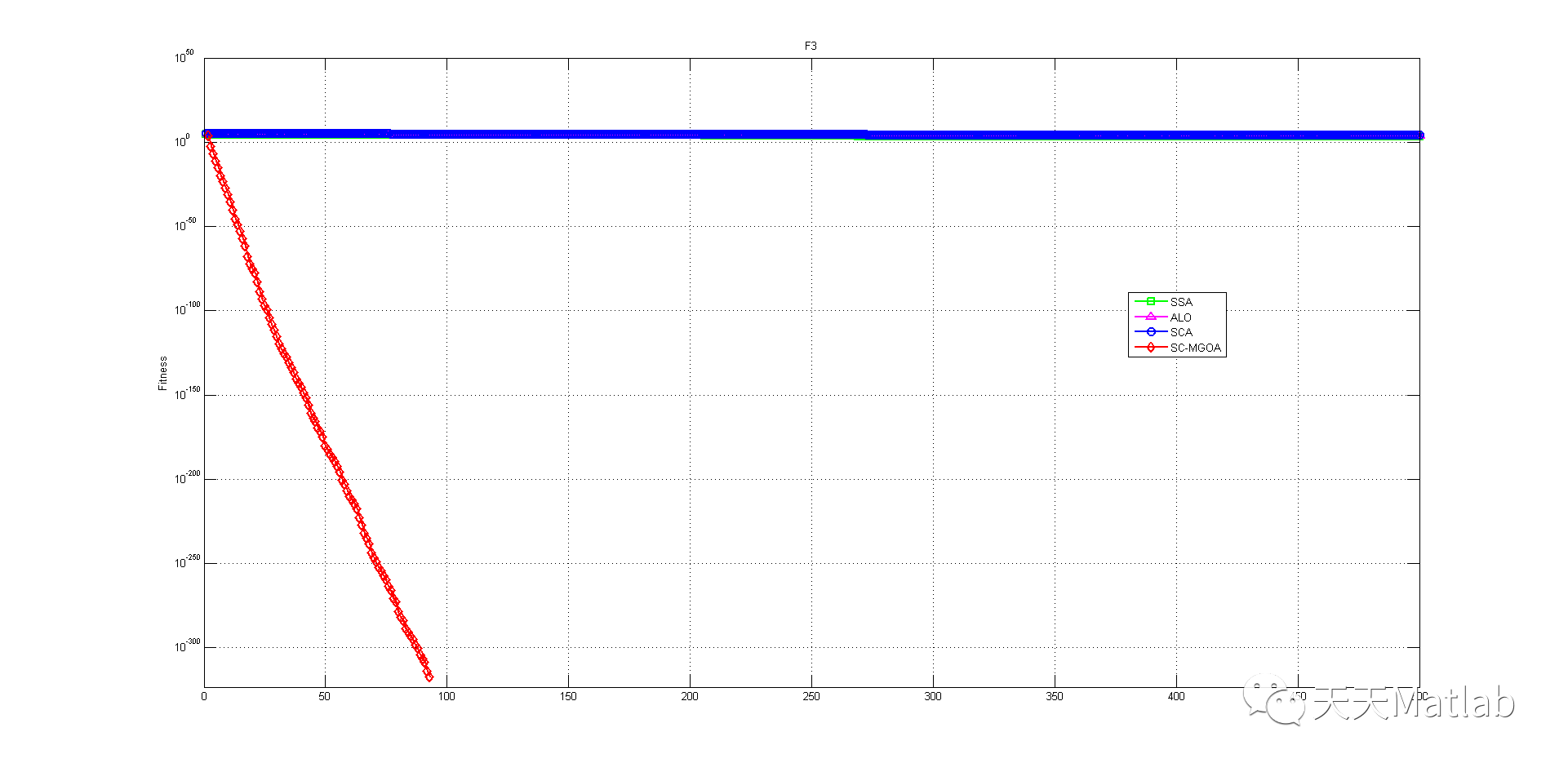
3 仿真结果

4 参考文献

[1]李洋州, 顾磊. 基于曲线自适应和模拟退火的蝗虫优化算法[J]. 计算机应用研究, 2019, 36(12):7.

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。