1.二叉树的概念

? ? ? ?二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

（1）若它的左子树不为空，则左子树上所有节点的值都小于根节点的值。

（2）若它的右子树不为空，则右子树上所有节点的值都大于根节点的值，它的左右子树也分别为二叉搜索树。

2.搜索二叉树的简单操作

2.1查找val

//构建节点
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node(int val) {
        this.val = val;
    }
}

public class BinarySearchTree {
    public Node root = null;


    public Node search(int key) {
        Node cur = root;
        while (cur != null) {
            if(cur.val < key) {
                cur = cur.right;
            }else if(cur.val == key) {
                return cur;
            }else {
                cur = cur.left;
            }
        }
        return null;//代表没有这个数据
    }

2.2插入节点

//插入新节点 
public boolean insert(int val) {
        if(root == null) {
            root = new Node(val);
            return true;
        }

        Node cur = root;//指向根节点
        Node parent = null;//指向根节点的父亲节点，保存cur的上一个节点
        while (cur != null) {
            if(cur.val < val) {
                parent = cur;
                cur = cur.right;
            }else if(cur.val == val) {
                return false;//不能有相同的数据
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
        Node node = new Node(val);//定义新节点
        if(parent.val < val) {
            parent.right = node;
        }else {
            parent.left = node;
        }
        return true;
    }

2.3删除节点

删除节点主要有以下3种情况：

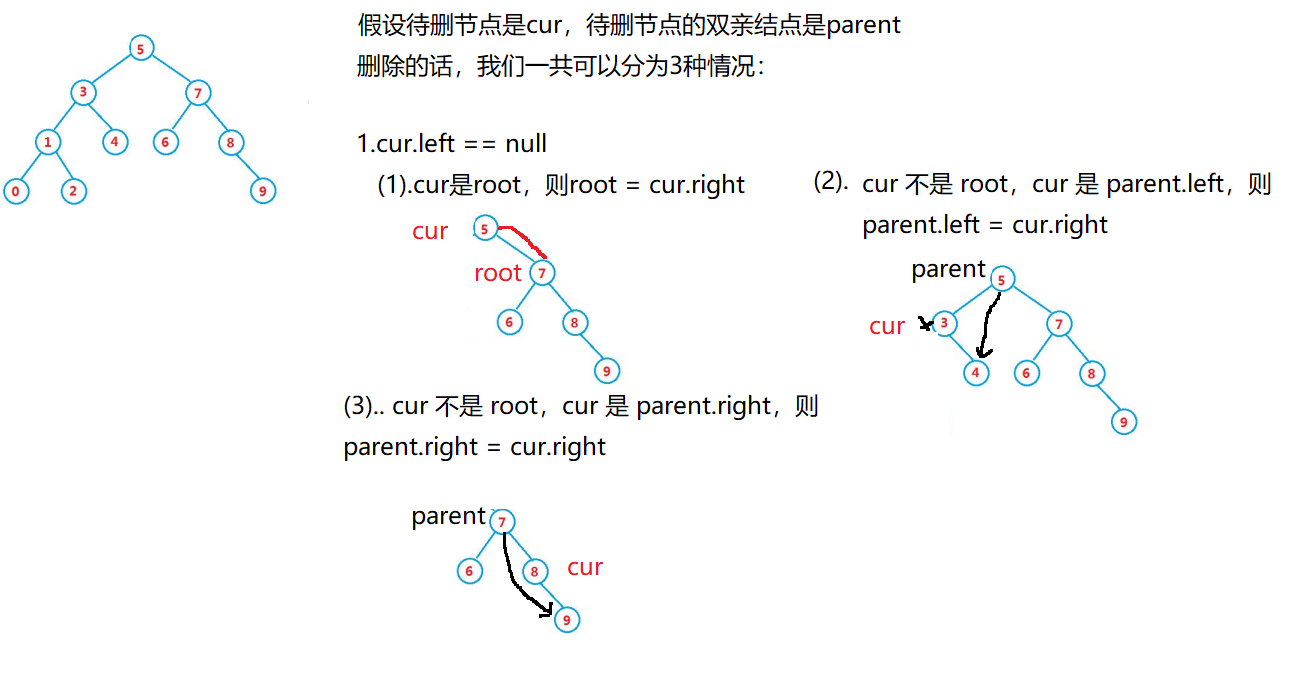
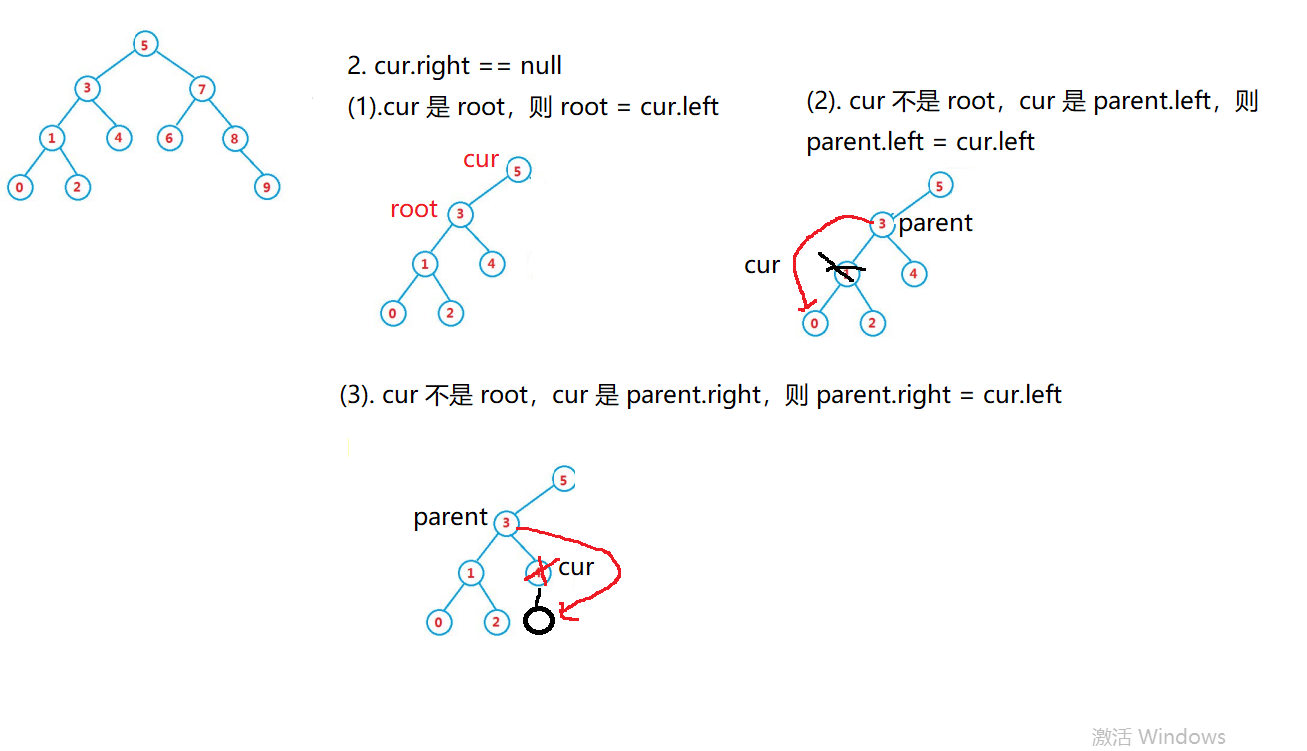
代码展示：

  public void remove(int key) {
        Node cur = root;
        Node parent = null;
        while (cur != null) {
            if(cur.val == key) {
                //这里开始删除
                removeNode(cur,parent);
                break;
            }else if(cur.val < key) {
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
    }

    public void removeNode(Node cur,Node parent) {
        if(cur.left == null) {
            if(cur == root) {
                root = cur.right;
            }else if(cur == parent.left) {
                parent.left = cur.right;
            }else {
                parent.right = cur.right;
            }
        }else if(cur.right == null) {
            if(cur == root) {
                root = cur.left;
            }else if(cur == parent.left) {
                parent.left = cur.left;
            }else {
                parent.right = cur.left;
            }
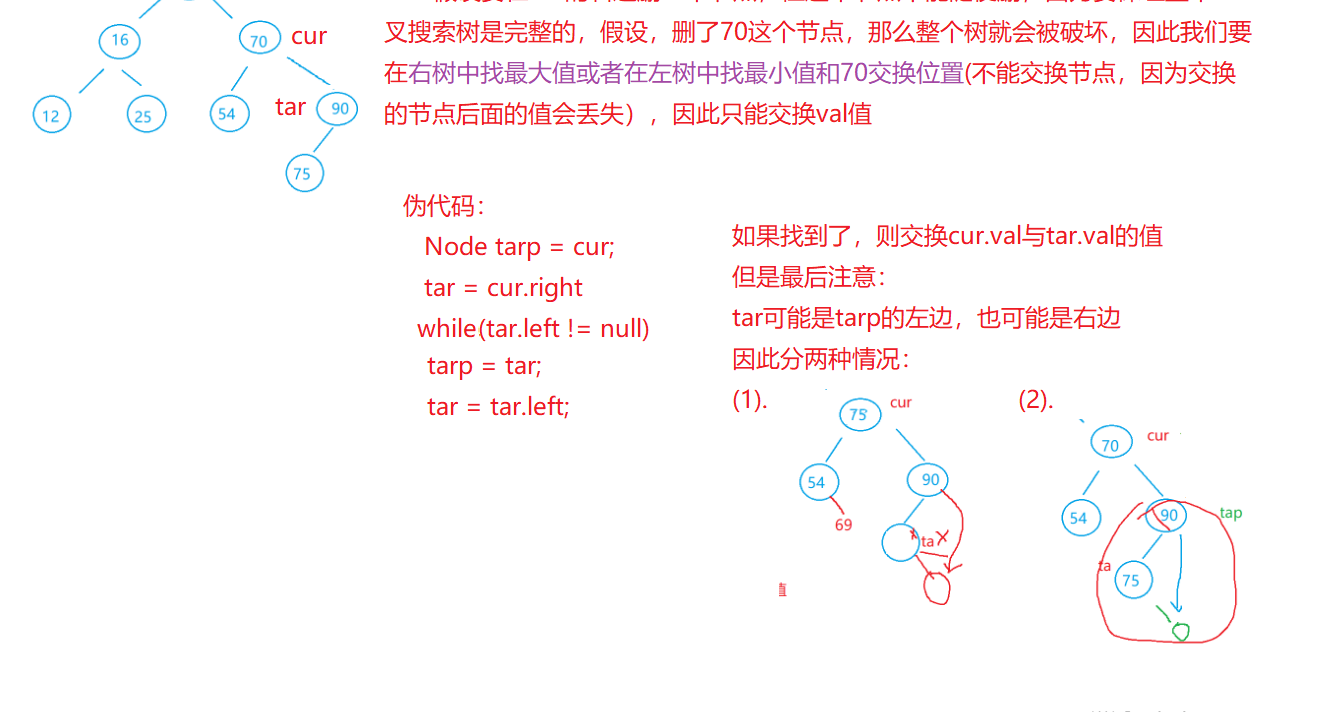
        }else {
            Node targetParent = cur;
            Node target = cur.right;
            while (target.left != null) {
                targetParent = target;
                target = target.left;
            }
            cur.val = target.val;
            if(target == targetParent.left) {
                targetParent.left = target.right;
            }else {
                targetParent.right = target.right;
            }
        }
    }

?2.4测试代码正确性

先写一个中序遍历，因为中序遍历是有序的，符合搜索二叉树

public void inOrder(Node root) {
        if(root == null) return;
        inOrder(root.left);
        System.out.print(root.val+" ");
        inOrder(root.right);

测试过程：

 public static void main(String[] args) {
        int[] array = {10,8,19,3,9,4,7};
        BinarySearchTree binarySearchTree = new BinarySearchTree();
        for (int i = 0; i < array.length; i++) {
            binarySearchTree.insert(array[i]);
        }
        binarySearchTree.inOrder(binarySearchTree.root);
        System.out.println("插入重复的数据");
        System.out.println(binarySearchTree.insert(3));
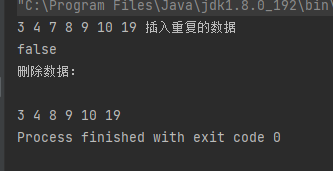
        System.out.println("删除数据：");
        binarySearchTree.remove(7);
        System.out.println();
        binarySearchTree.inOrder(binarySearchTree.root);

    }