(1)CORDIC算法的圆周系统之旋转模式原理简介
CORDIC算法是一种兼容速度快、精度高和方便硬件资源实现的综合方法。它使用多次预定角度的不断旋转来逼近初值角度的近似逼近方法。CORDIC算法有3种旋转系统:圆周系统、线性系统和双曲系统。每种系统下都有两种工作模式:旋转模式和向量模式。其每个系统每种模式下的应用情况如下:
表一:CORDIC算法的3种系统和2种不同模式应用情况
| 旋转模式 | 向量模式 | |
|---|---|---|
| 圆周系统 | 计算sin、cos | 计算tan-1 |
| 线性系统 | 计算乘法 | 计算除法 |
| 双曲系统 | 计算cosh、sinh | 计算tanh-1 |
CORDIC算法圆周系统的旋转模式,可以实现正弦函数和余弦函数的运算。相应的迭代运算如式所示:

其中,

经过n(n趋近于无穷)次旋转,得到的最终结果为
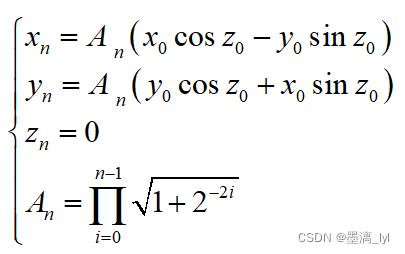
由上式可知,当初始化角度x0=1/An,y0=0时,其中An=1.64676可得出:

按上述步骤迭代,即可在x,y的输出值中得到输入值z0的正弦余弦值。但该cordic算法的局限性在于输入值度数范围为[-99.8829,99.8829],但在设计的场合中需要目标旋转角度可覆盖整个周期,则需要在本cordic算法的基础上按三角函数的对称性进行预处理。
(2)旋转模式下CORDIC算法的FPGA实现
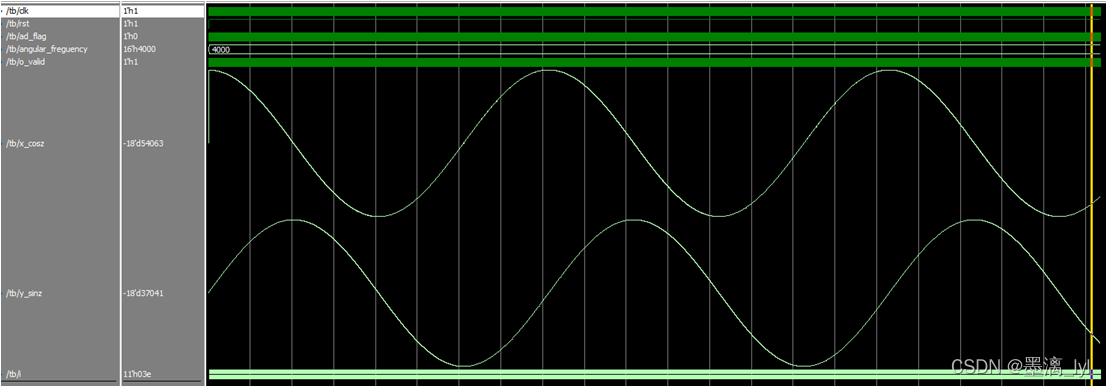
下图为设计的CORDIC算法的输入输出端口,i_valid信号为输入有效信号,当输入信号有效后,将该信号拉高一个时钟周期后,模块开始对zin中的数据计算正弦余弦值;x_cosz,y_sinz分别表示向量的余弦值和正弦值;o_valid信号则是当输出有效后,拉高一个时钟周期。完整CORDIC算法代码见评论区链接。
(3) CORDIC算法误差分析
在上述的cordic算法的输入中,zi的输入位宽都是16bit,为了分析cordic算法计算误差情况,对cordic计算出的正弦余弦值与实际的值作对比,误差散点图如下图所示:
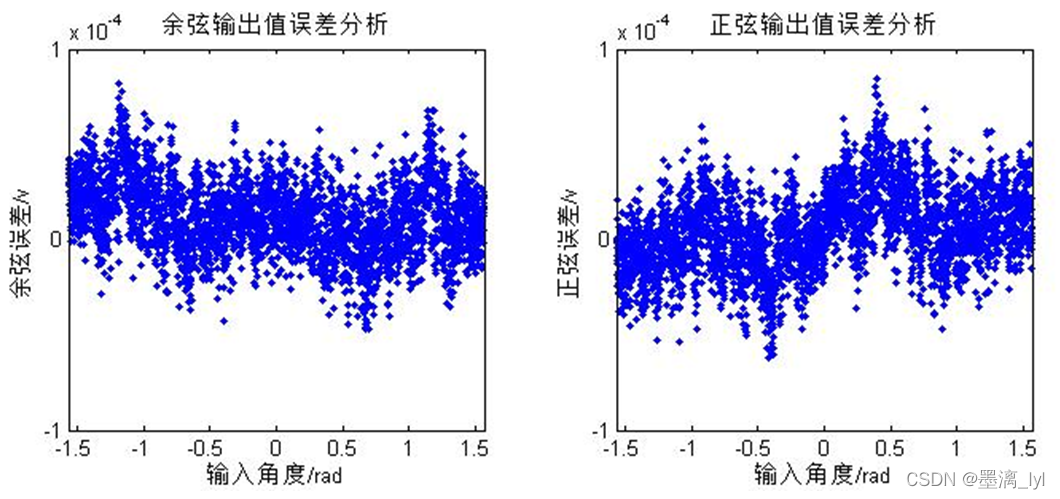
由上图可知,运用cordic算法计算出的结果中,正弦余弦值误差范围均在10的-4次方以内,该CORDIC算法计算精度达到要求。
(4)基于CORDIC算法的DDS实现
顶层文件的输入输出端口如下图所示:

其中clk为运算的主频时钟,必须采样100Mhz的时钟输入;ad_flag表示adc采集信号有效的标志位,即每在ad_flag的上升沿,锁相放大器就读取一次采集的数据,保证了参考信号的采样频率与ADC信号采样频率一致;16bit的angular_freguency输入信号为要生成的正弦余弦信号的角频率,其小数位位宽为12bit;输出的正弦余弦值均为18bit 小数位位宽16bit。
modelsim仿真分析图如下: