[数据结构与算法]字符串匹配算法（KMP算法JAVA版）

目录

暴力匹配

KMP算法

暴力匹配

暴力算法就是 普通模式的匹配算法  bf算法就是将目标的字符串 的第一个字符与模式的第一个字符进行匹配，相等的话就继续比较第二个字符是否是匹配的，依次进行下去，如果不匹配的话 就进行回退至第二个字符重新进行匹配。直到得到最后的结果。

?

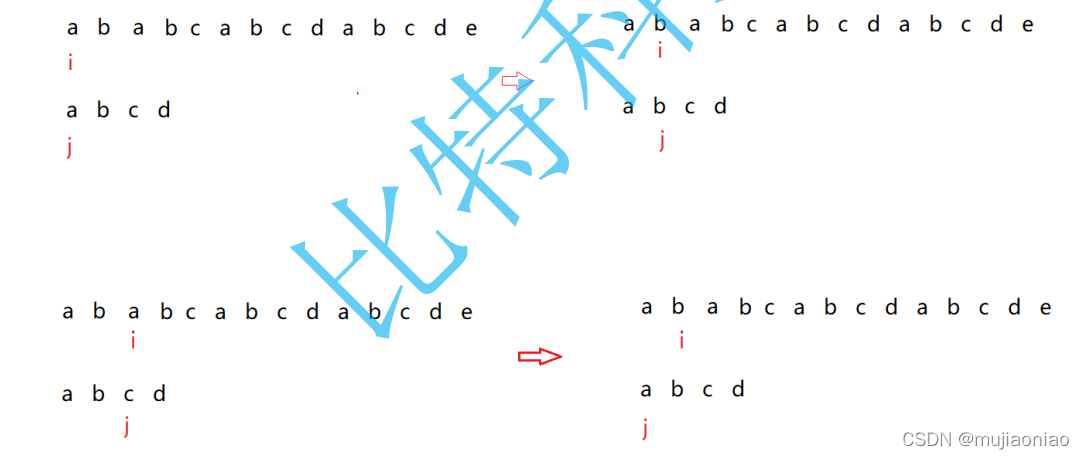
匹配失败的话 就回退至最初i下标的下一位

public class BF1 {
 ?  public static int BF(String str, String sub){
 ? ? ?  if (str == null || sub == null) return  -1;
 ? ? ?  int strLen = str.length();
 ? ? ?  int subLen = sub.length();
 ? ? ?  int i = 0;
 ? ? ?  int j = 0;
 ? ? ?  while (i < strLen && j <subLen){
 ? ? ? ? ?  if (str.charAt(i) == sub.charAt(j)){
 ? ? ? ? ? ? ?  i++;
 ? ? ? ? ? ? ?  j++;
 ? ? ? ? ?  }else {
 ? ? ? ? ? ? ?  i = i -j +1; // i-j就是回退到i原来的位置  +1 就是i的下一位开始。同时恢复j的值
 ? ? ? ? ? ? ?  j = 0;
 ? ? ? ? ?  }
 ? ? ?  }
 ? ? ?  if (j >= subLen){
 ? ? ? ? ?  return i-j; //此时已经找到该下标
 ? ? ?  }
 ? ? ?  return -1; //没有找到
 ?  }
?
 ?  public static void main(String[] args) {
 ? ? ?  System.out.println(BF("absjhsjhdsnn","ab"));//0
 ? ? ?  System.out.println(BF("abscbcbcbcbjhsjhsdsdkjn","bcb"));//4
 ?  }
?
}

KMP算法

KMP算法是一种改进的字符串匹配的算法它的核心就是利用匹配失败后的 信息，尽量的减少子串与主串的匹配次数 可以达到一个快速匹配的机制，
具体的实现是靠着一个next()函数晒西安，KMP的时间复杂度就是O(m+n);

区别：KMP的最大好处就是，上述的主串当中的i下标不会进行回退，并且j也不用每次都移动到最初始的位置中。

而要想到达这样的效果就必须引出next数组：next[j] = k;

对于k值的要求：
1.规则：找到匹配成功部分的两个相等的真子串（不包含本省），一个以下标的0字符开始，而另一个以下标的j-1下标字符作为结尾（注意）
2.不管什么数据 next[0] = -1; next[1] =0; 这里的[]数字就是子串的下标, " = " 后面的就是对应的k值。

java实现

public class KMP1 {
?
 ?  public static void getNext(int[] next, String sub){
 ? ? ?  next[0] = -1;
 ? ? ?  next[1] = 0 ;
 ? ? ?  int i = 2 ; // next数组的下标
 ? ? ?  int k = 0 ;
 ? ? ?  while (i < sub.length()){
 ? ? ? ? ?  //说明next数组没有遍历完
 ? ? ? ? ?  if ((k == -1) || sub.charAt(k) == sub.charAt(i-1)){ // 此时k等于-1说明走到了 sub的第一位前一位 所以就必须让k++；否则会越界
 ? ? ? ? ? ? ?  next[i] = k+1; // 由k的规律中可得
 ? ? ? ? ? ? ?  i++;
 ? ? ? ? ? ? ?  k++;
 ? ? ? ? ?  }else {
 ? ? ? ? ? ? ?  k = next[k];
 ? ? ? ? ?  }
 ? ? ?  }
 ?  }
?
?
?
?
 ?  public static  int KMP(String str ,String sub ,int pos){
 ? ? ?  int i = pos;
 ? ? ?  int j = 0;
 ? ? ?  int strLen = str.length();
 ? ? ?  int subLen = sub.length();
?
 ? ? ?  int [] next = new int[subLen];
 ? ? ? ? getNext(next,sub);
 ? ? ? while (i < strLen && j < subLen){
 ? ? ? ? ? if ((j == -1) || (sub.charAt(j) == str.charAt(i))){ // 当j等于-1的时候说明走到了 sub的第一位前一位，所以需要重新让j指向sub的0下标。
 ? ? ? ? ? ? ? i++;
 ? ? ? ? ? ? ? j++;
 ? ? ? ? ? ? ? // 满足条件向后走 并且进行匹配
 ? ? ? ? ? }else {
 ? ? ? ? ? ? ? j = next[j]; // 没有匹配上的情况下 j就进行回退到 next数组中的下标位置。
 ? ? ? ? ? }
 ? ? ? }
 ? ? ? if (j >= subLen){
 ? ? ? ? ? return i-j;
 ? ? ? }else {
 ? ? ? ? ? return -1;
 ? ? ? }
 ?  }
?
 ?  public static void main(String[] args) {
 ? ? ?  System.out.println(KMP("bbbbccccbhbbchs","bbc",0));//2
 ? ? ?  System.out.println(KMP("aabcbcbcbbccccbhbbchs","bbbc",0));//-1
 ? ? ?  System.out.println(KMP("baabbaabccccbhbbbbbbbchs","aabc",0));//5
?
 ?  }
 ? ?
}