[数据结构与算法]C++刷题之旅（12）

LeetCode算法入门（第十二天）

动态规划

https://juejin.cn/post/6951922898638471181

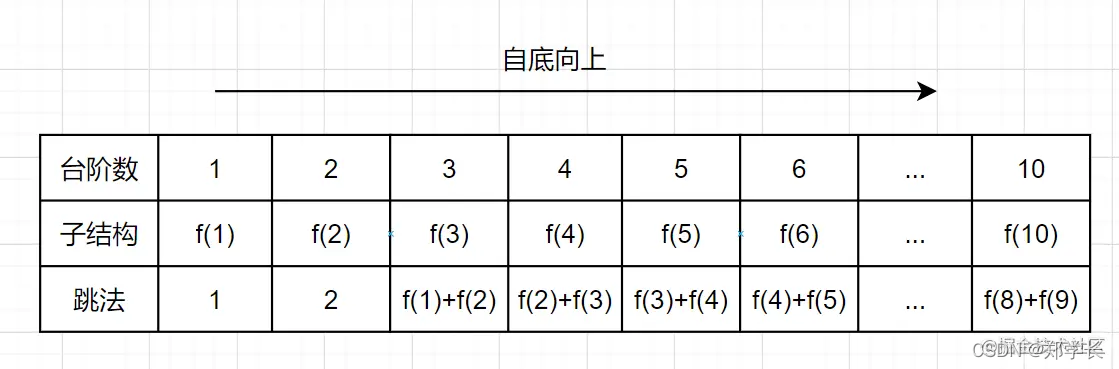
77.爬楼梯

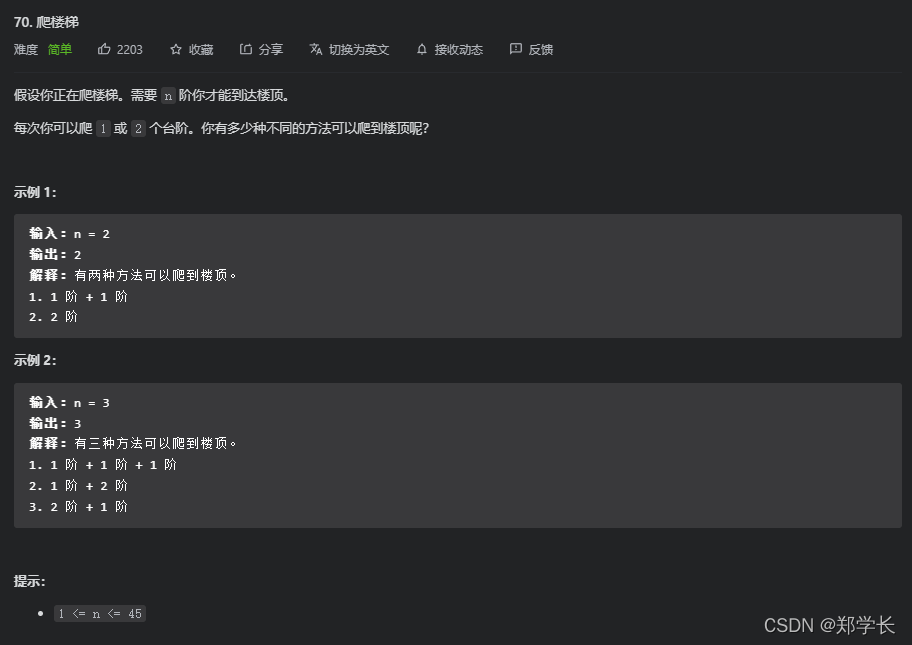
解法：

class Solution {
public:
    int climbStairs(int n) {
        int ans = 0;
        if(n <= 2){
            ans = n;
            return ans;
        }
        int a = 1;
        int b = 2;
        for(int i = 3; i <= n; i++){
            ans = a + b;
            a = b;
            b = ans;
        }
        return ans;
    }
};

198.打家劫舍

假设是专业小偷

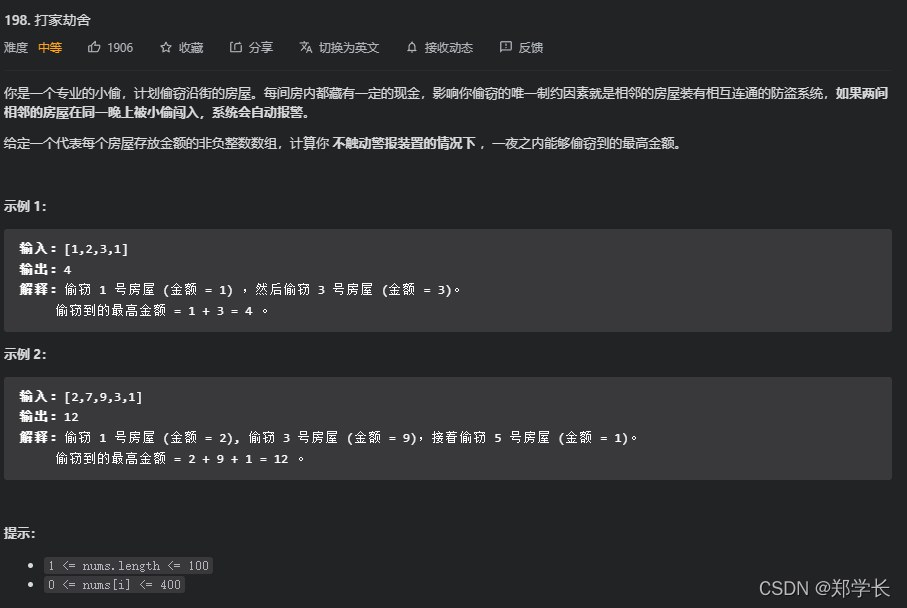
解法：初始化dp数组是个容易忽视的点。

class Solution {
public:
    int rob(vector<int>& nums) {
        int size = nums.size();
        vector<int> S(size, 0);
      
        if(nums.empty()){
            return 0;
        }
       if(size == 1){
           return nums[0];
       }

       S[0] = nums[0];
       S[1] = max(nums[0], nums[1]);
        for(int i = 2; i < size; i++){
            S[i] = max(S[i-1], S[i-2] + nums[i]);  //返回最大值
        }
        return S[size - 1];   
    }
};

120.三角形最小路径和

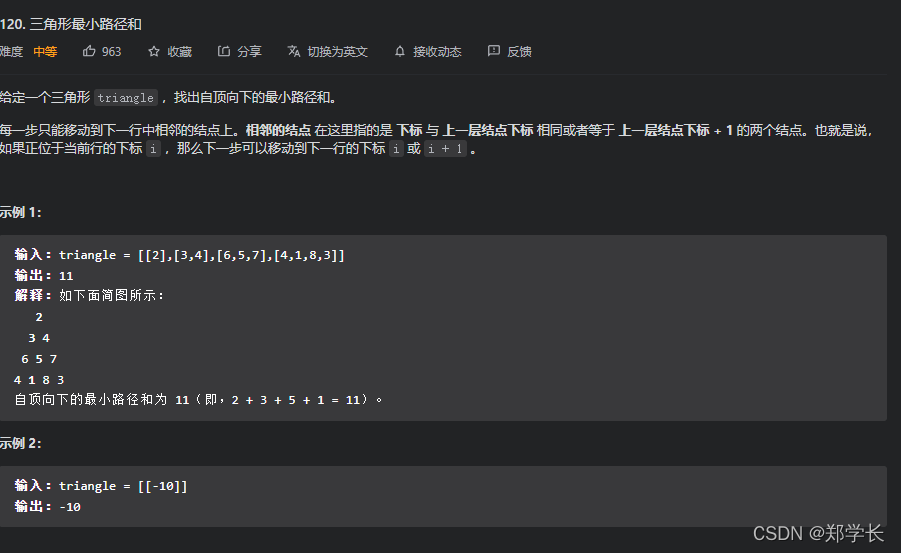
解法：当我们考虑点$f_{[i][j]}$时，它是由$f_{[i?1][j]}$或者$f_{[i?1][j?1]}$移动而来，于是递推公式就确定下来，但是还有一些特殊条件需要注意，结点是最左侧的时候，以及i=j时。

class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) {
        int n = triangle.size();
        vector<vector<int>> f(n, vector<int>(n));   //初始化dp
        f[0][0] = triangle[0][0];
        for (int i = 1; i < n; ++i) {
            f[i][0] = f[i - 1][0] + triangle[i][0];    //当前结点位于最左侧
            for (int j = 1; j < i; ++j) {
                f[i][j] = min(f[i - 1][j - 1], f[i - 1][j]) + triangle[i][j];
            }
            f[i][i] = f[i - 1][i - 1] + triangle[i][i];
        }
        return *min_element(f[n - 1].begin(), f[n - 1].end());   //min-element返回容器中的最小值的索引位置
    }
};