[数据结构与算法]二叉树的对称问题

1. 对称二叉树

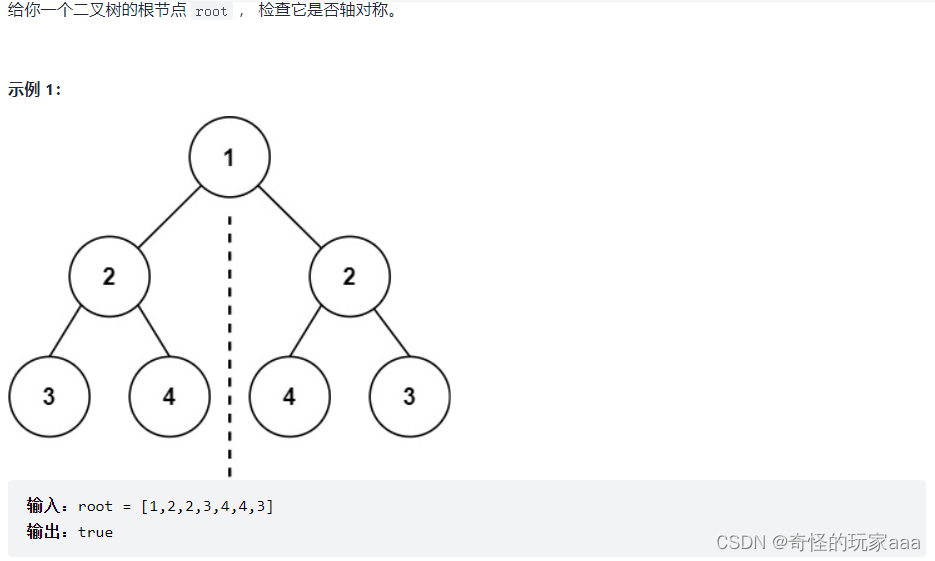
对称二叉树

思路：
1.先将根节点的左右节点入队。
2.出队，比较两个节点的值是否相等
3.若相等，则当前左节点的左节点入队，当前右节点的右节点入队，当前左节点的右节点入队，当前右节点的左节点入队。若不相等，返回false。
4.注意：当节点为空时，跳出此次循环。。。。。。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isSymmetric(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();//存放节点
        
        queue.offer(root.left);
        queue.offer(root.right);

        while(!queue.isEmpty()){
            TreeNode Lnode = queue.poll();
            TreeNode Rnode = queue.poll();
            if(Lnode==null&&Rnode==null) continue;
            if(Lnode==null&&Rnode!=null) return false;
            if(Lnode!=null&&Rnode==null) return false;
            if(Lnode.val!=Rnode.val) return false;
            // 两个节点值相等
            queue.offer(Lnode.left);  //外层
            queue.offer(Rnode.right);//外层

            queue.offer(Lnode.right);//内层
            queue.offer(Rnode.left);//内层
        }
        return true;//当不满足循环时，返回true

    }
}

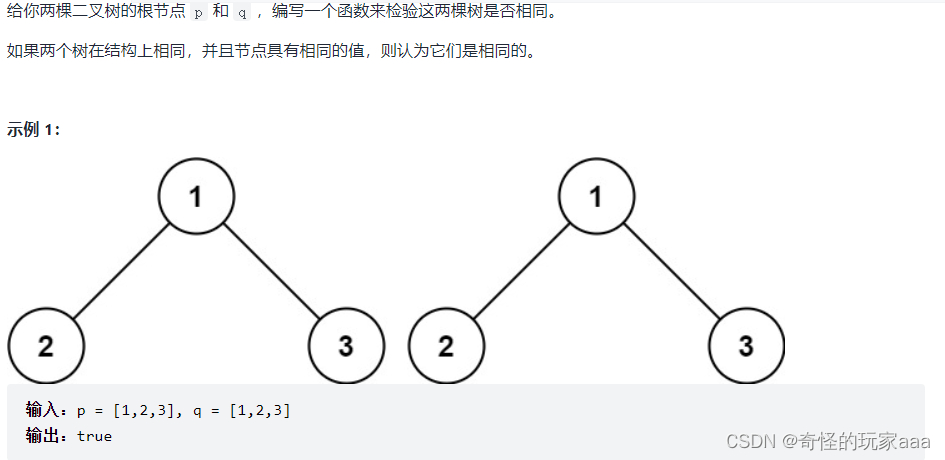
2.相同的树

相同的树

思路：
1.若两棵树不为空，将两棵树的根节点入队
2.若值相等，将p树的左节点入队，q树的左节点入队，p树的右节点入队，q树的右节点入队。
3.若当时左右根节点均为null，说明已经遍历完成，则退出本次循环

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        //先判断根节点是否为空
        if(p==null&&q==null) return true;
        if(p==null||q==null) return false;
        //根节点不为空
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(p);
        queue.offer(q);

        while(!queue.isEmpty()){
            //注意取出结点，否则造成死循环
            TreeNode Lnode = queue.poll();//取出根节点
            TreeNode Rnode = queue.poll();

            if(Lnode==null&&Rnode!=null) return false;
            if(Lnode!=null&&Rnode==null) return false;
            if(Lnode==null&&Rnode==null) continue;
            if(Lnode.val!=Rnode.val) return false;

            //节点不为空，且值相等
            queue.offer(Lnode.left);
            queue.offer(Rnode.left);
            queue.offer(Lnode.right);
            queue.offer(Rnode.right);
        }
        return true;
    }
}

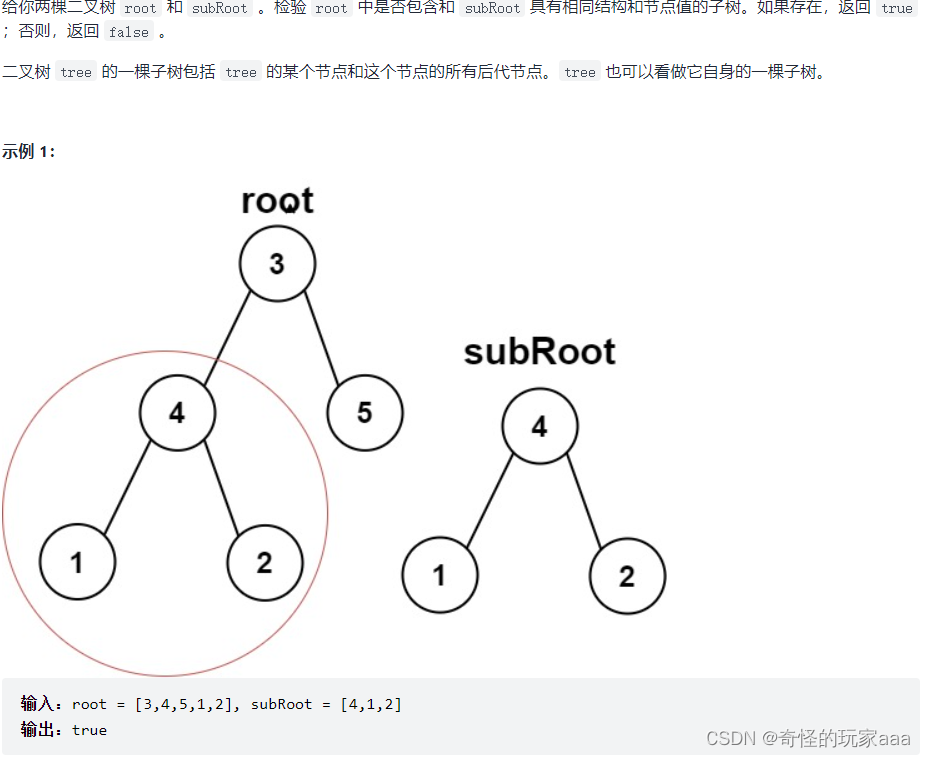
3.另一棵树的子树

另一棵树的子树

双重递归

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        
         if(root==null &&subRoot ==null) return true;
         if(root==null||subRoot==null) return false;
         
         //根节点不为空
         Queue<TreeNode> queue = new LinkedList<>();
         queue.offer(root); //根节点入队
         while(!queue.isEmpty()){
            TreeNode temp = queue.poll();//取出根节点

            if(isSame(temp,subRoot)) return true;
            //如果是false，继续遍历
            if(temp.left!=null) queue.add(temp.left);
            
            if(temp.right!=null) queue.add(temp.right);
         }
         return false;
                 
    }

    public boolean isSame(TreeNode node1,TreeNode node2){
        if(node1==null&&node2==null) return true;
        if(node1==null||node2==null||node1.val!=node2.val) return false;
        //当前节点不为空且值相等,继续遍历
        return isSame(node1.left,node2.left)&&isSame(node1.right,node2.right);
    }
}