前言

解决双指针问题四种常用思想：

普通双指针（two sum），一般两个for循环，外层i和内层j可以认为是普通的双指针；
左右指针(二分搜索)：需要两个指针，一个指向开头，一个指向末尾，然后向中间遍历，直到满足条件或者两个指针相遇；
快慢指针：需要两个指针，开始都指向开头，根据条件不同，快指针走得快，慢指针走的慢，直到满足条件或者快指针走到结尾；
滑动窗口。

普通双指针

1. 两数之和

在这里插入图片描述
一般两个for循环，外层i和内层j可以认为是普通的双指针；本题进行了空间换时间的优化，因为内层的for循环做了重复工作，可以用一个hashmap进行优化。

class Solution {
    //method 1
    // public int[] twoSum(int[] nums, int target) {
    //     for (int i = 0; i < nums.length; i++) {
    //         for (int j = 0; j < i; j++) {
    //             if (nums[i] + nums[j] == target) {
    //                 return new int[]{j, i};
    //             }
    //         }
    //     }
    //     return new int[]{-1, -1};
    // }
    //method 2
    public int[] twoSum(int[] nums, int target) {
        HashMap<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            if (map.containsKey(target - nums[i])) {
                return new int[]{map.get(target - nums[i]), i};
            }
            map.put(nums[i], i);
        }
        return new int[]{-1, -1};
    }
}

左右指针

在有序数组 中搜索?个元素 target，返回该元素对应的索引。

1.寻找?个数（基本的?分搜索）

搜索?个数，如果存在，返回其索引，否则返回 -1 。

public int binary_search(int[] nums, int target) {
    int left = 0, right = nums.length - 1;//搜索区间为[left,right]
    while (left <= right) {//终止条件为搜索到[right,left]
        int mid = left + (right - left) / 2;//不用mid=(left+right)/2 是为了防止left+right溢出，>Integer.Maxvalue就会边为负数
        if (nums[mid] < target) {
            left = mid + 1;//缩小左边界，区间[mid+1，right]
        } else if (nums[mid] > target) {
            right = mid - 1;//缩小右边界，区间[left,mid-1]
        } else {
            return mid;//搜索到目标区间，nums[mid]=target，return mid
        }
    }
    return -1; //遍历数组没有找到target
}

2.寻找左侧边界的?分搜索

当目标元素 target 不存在数组 nums 中时， 搜索左侧边界的?分搜索的返回值可以做以下?种解读： 
1 、返回的这个值是 nums 中大于等于 target 的最小元素索引。 
2、 返回的这个值是 target 应该插入在 nums 中的索引位置。 
3、 返回的这个值是 nums 中小于 target 的元素个数。
?如在有序数组 nums = [2,3,5,7] 中搜索 target = 4， 搜索左边界的?分算法会返回 2

寻找左侧第一个2
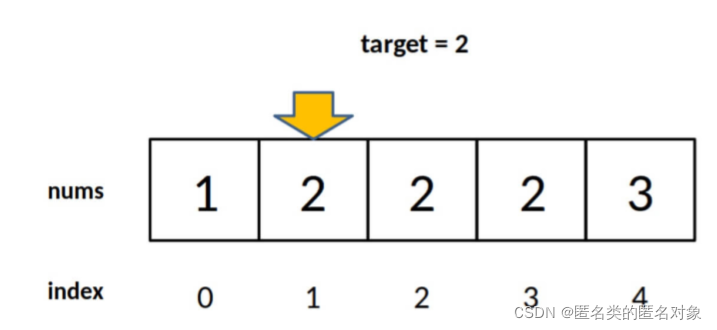
12312222222222222222222
left越界情况
在这里插入132

public int left_bound(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else{// 锁定左侧边界，收缩右侧边界,即nums[mid]>=target
            right = mid - 1;
        }
    }
    // 最后要检查 left 越界的情况
    if (left >= nums.length || nums[left] != target) return -1;
    return left;
}

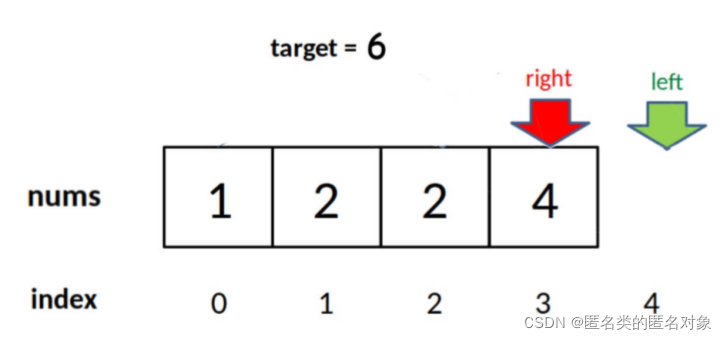
3.寻找右侧边界的?分搜索

right越界情况
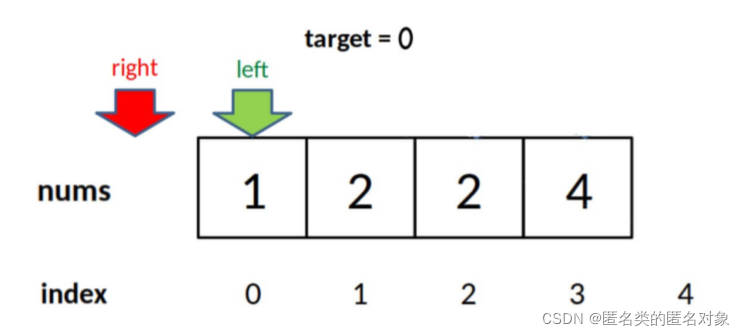
在这里插入图片描述

int right_bound(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] <= target) {//锁定右侧边界，收缩左侧边界
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }
    // 最后要检查 right 越界的情况
    if (right < 0 || nums[right] != target) return -1;
    return right;
}

704. 二分查找

在这里插入图片描述

public int search(int[] nums, int target) {
    return binary_search(nums, target);
}

34. 在排序数组中查找元素的第一个和最后一个位置

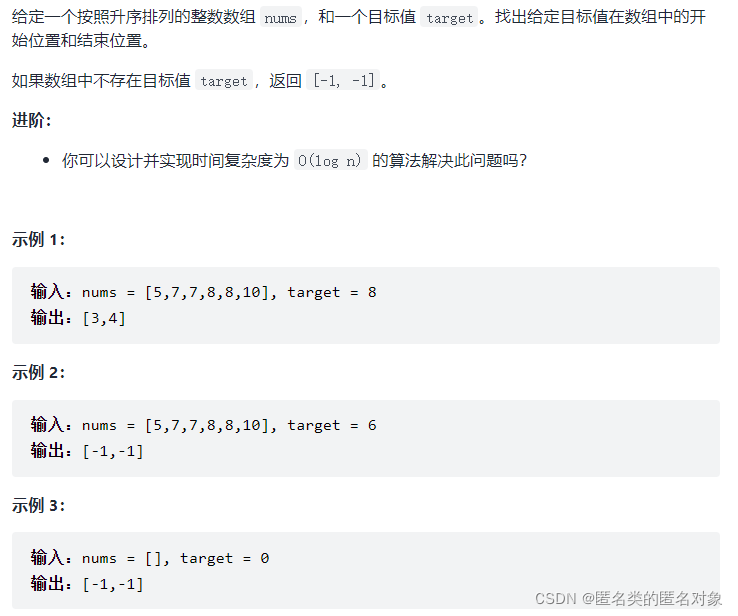
在这里插入图片描述

public int[] searchRange(int[] nums, int target) {
    return new int[]{left_bound(nums, target), right_bound(nums, target)};
}

35. 搜索插入位置

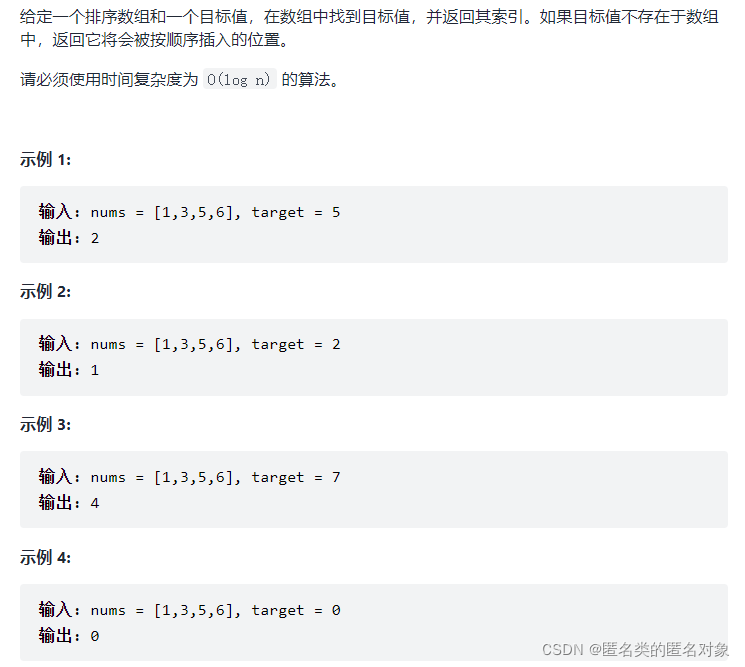
在这里插入图片描述

	public int searchInsert(int[] nums, int target) {
        return left_bound(nums, target);
    }

快慢指针

141. 环形链表（简单）

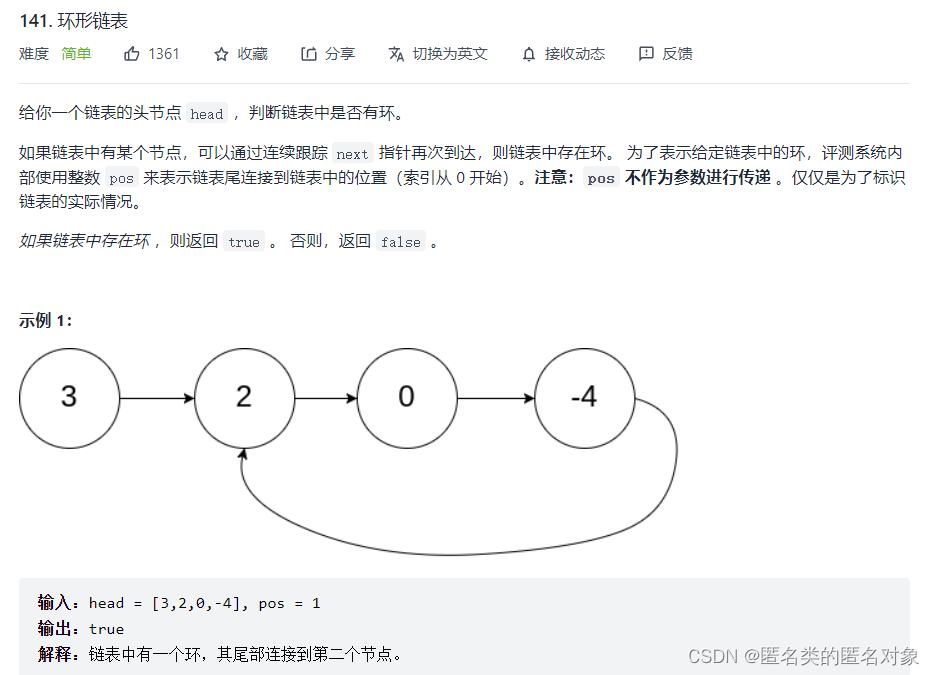
在这里插入图片描述

public boolean hasCycle(ListNode head) {
        ListNode slow = head, fast = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) {
                return true;
            }
        }
        return false;
    }

142. 环形链表 II(中等)

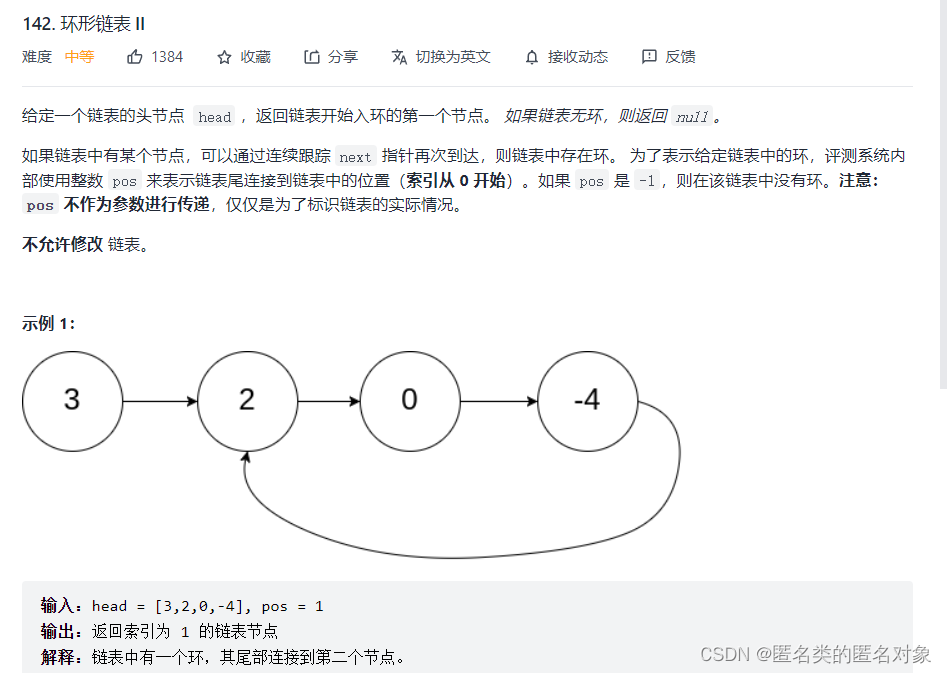
在这里插入图片描述

public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode slow = head, fast = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) {
                break;
            }
        }
        if (fast == null || fast.next == null) {
            return null;
        }
        slow = head;
        while (slow != fast) {
            slow = slow.next;
            fast = fast.next;
        }
        return slow;
    }
}