简单凸优化笔记
凸函数和凸集
- 凸函数上方区域为凸集
- 函数上方区域为凸集,则函数为凸函数
凸集
集合
C
C
C任意两点间线段都在集合
C
C
C里,则称集合
C
C
C为凸集
?
x
1
,
x
2
∈
C
,
θ
∈
[
0
,
1
]
则
θ
x
1
+
(
1
?
θ
)
x
2
∈
C
\forall x_{1},x_{2}\in C, \theta\in[0,1]\\ 则\theta x_{1}+(1-\theta)x_{2}\in C
?x1?,x2?∈C,θ∈[0,1]则θx1?+(1?θ)x2?∈C
拓展
?
x
1
,
.
.
.
,
x
k
∈
C
,
θ
i
∈
[
0
,
1
]
且
∑
θ
i
=
1
则
∑
θ
i
x
i
∈
C
\forall x_{1},...,x_{k}\in C, \theta_{i}\in[0,1]且\sum\theta_{i}=1\\ 则\sum\theta_{i}x_{i}\in C
?x1?,...,xk?∈C,θi?∈[0,1]且∑θi?=1则∑θi?xi?∈C
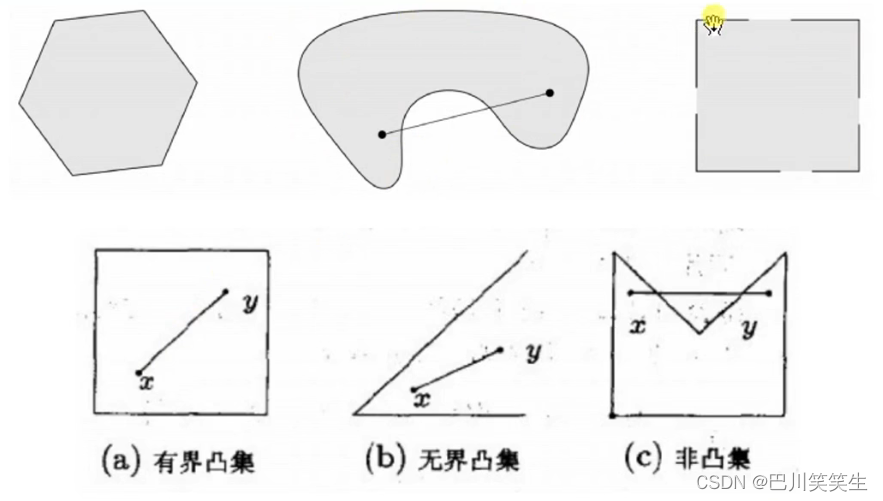
凸多边形是凸集,边界缺失不是凸集
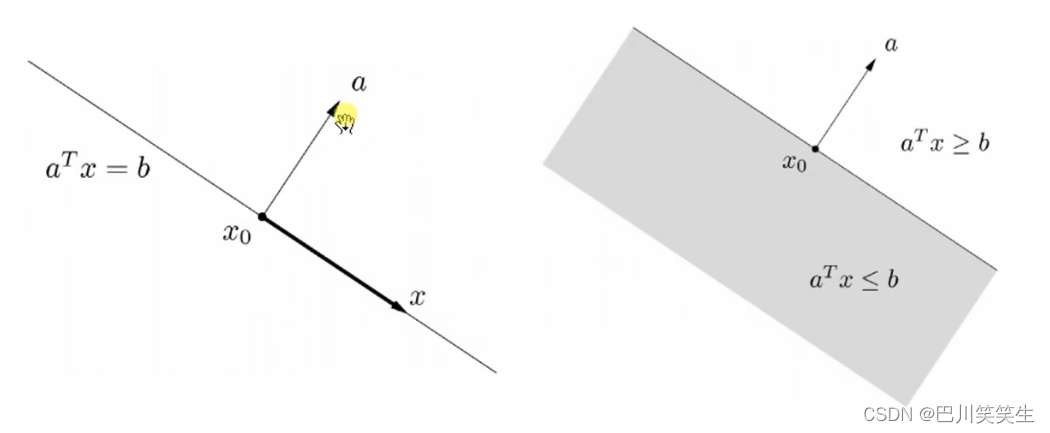
超平面和半空间
超平面
{ x ∣ a T x = b } \{x|a^{T}x=b\} {x∣aTx=b}
半空间
{ x ∣ a T x ≤ b } { x ∣ a T x ≥ b } \{x|a^{T}x\leq b\}\\ \{x|a^{T}x\geq b\} {x∣aTx≤b}{x∣aTx≥b}
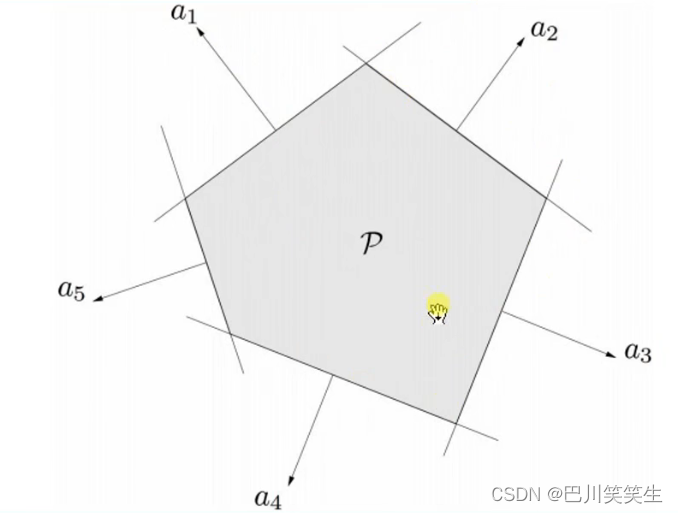
多面体
多面体是有限个半空间和超平面交集
P
=
{
x
∣
a
j
T
x
≤
b
j
,
c
i
T
x
=
d
i
}
P=\{x|a_{j}^{T}x\leq b_{j},c_{i}^{T}x=d_{i}\}
P={x∣ajT?x≤bj?,ciT?x=di?}
仿射集(如超平面,直线),射线,线段,半空间都是多面体
多面体是凸集
有界多面体称多胞形
保持凸性运算
- 集合交运算
定义证明
- 仿射变换
- 伸缩
- 平移
- 投影
f ( x ) = A x + b , A ∈ R m × n , b ∈ R m f : R n → R m f ( S ) = { f ( x ) ∣ x ∈ S } S 为 凸 集 → f ( S ) 为 凸 集 f ( S ) 为 凸 集 → S 为 凸 集 f(x)=Ax+b,A\in R^{m\times n},b\in R^{m}\\ f:R^{n}\rightarrow R^{m} \quad f(S)=\{f(x)|x\in S\}\\ S为凸集\rightarrow f(S)为凸集\\ f(S)为凸集\rightarrow S为凸集\\ f(x)=Ax+b,A∈Rm×n,b∈Rmf:Rn→Rmf(S)={f(x)∣x∈S}S为凸集→f(S)为凸集f(S)为凸集→S为凸集
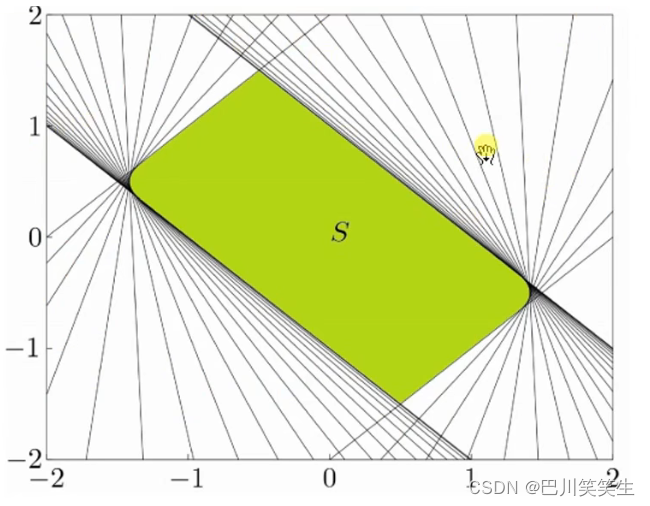
- 透视变换
透视函数对向量进行伸缩(规范)使最后一维的分量为一并舍弃
P
:
R
n
+
1
→
R
n
,
P
(
z
,
t
)
=
z
/
t
P:R^{n+1}\rightarrow R^{n}, P(z,t)=z/t
P:Rn+1→Rn,P(z,t)=z/t
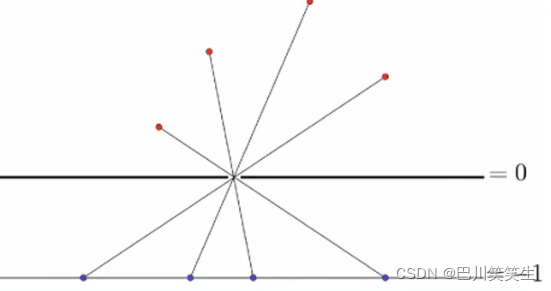
- 投射变换(线性分式变换)
透视和仿射的复合
g
:
R
n
→
R
n
+
1
g
(
x
)
=
[
A
c
T
]
x
+
[
b
d
]
A
∈
R
m
×
n
,
b
∈
R
m
,
c
∈
R
n
,
d
∈
R
g:R^{n}\rightarrow R^{n+1}\\ g(x)=\begin{bmatrix} A\\ c^{T} \end{bmatrix}x+ \begin{bmatrix} b \\ d \end{bmatrix}\\ A\in R^{m\times n},b\in R^{m},c\in R^{n},d\in R
g:Rn→Rn+1g(x)=[AcT?]x+[bd?]A∈Rm×n,b∈Rm,c∈Rn,d∈R
定义
f
f
f为线性分式函数
f
(
x
)
=
(
A
x
+
b
)
c
T
x
+
d
d
o
m
f
=
{
x
∣
c
T
x
+
d
>
0
}
f(x)=\frac{(Ax+b)}{c^{T}x+d}\\ dom f=\{x|c^{T}x+d>0\}
f(x)=cTx+d(Ax+b)?domf={x∣cTx+d>0}
若
c
=
0
,
d
>
0
c=0,d>0
c=0,d>0则
f
f
f为普通仿射函数
分割超平面
设
C
C
C和
D
D
D为两个不相交凸集,则存在超平面
P
P
P,
P
P
P可以将
C
C
C和
D
D
D分离
?
x
∈
C
,
a
T
x
≤
b
且
?
x
∈
D
,
a
T
x
≥
b
\forall x\in C,a^{T}x\leq b且\forall x\in D,a^{T}x\geq b
?x∈C,aTx≤b且?x∈D,aTx≥b
注意可以取等号
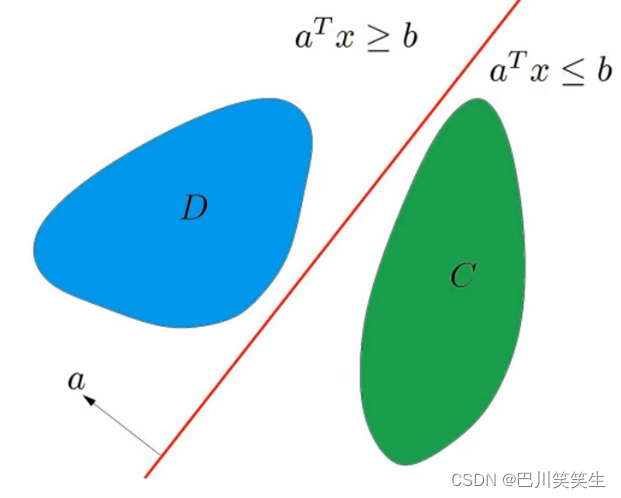
逆命题
若两个凸集 C C C和 D D D的分割超平面存在, C C C和 D D D不相交为假命题
加强条件
若两个凸集至少有一个是开集,那么当且仅当存在分割超平面,它们不相交
分割超平面构造
距离
两个集合距离为两个集合间元素的最短距离
构造
做距离中垂线
支撑超平面
设集合 C C C, x 0 x_{0} x0?为 C C C边界上的点。若存在 a ≠ 0 a\neq 0 a?=0,满足对任意 x ∈ C x\in C x∈C,都有 a T x ≤ a T x 0 a^{T}x\leq a^{T}x_{0} aTx≤aTx0?成立,则称超平面 { x ∣ a T x = a T x 0 } \{x|a^{T}x=a^{T}x_{0}\} {x∣aTx=aTx0?}为集合 C C C在点 x 0 x_{0} x0?处的支撑超平面
凸集边界任意一点都存在支撑超平面
反之,若一个闭的非中空(内部点不为空)集合,在边界上任意一点存在支撑超平面,则该集合为凸集
凸函数
若函数
f
f
f定义域
d
o
m
f
dom f
domf为凸集,且满足
?
x
,
y
∈
d
o
m
f
,
0
≤
θ
≤
1
有
f
(
θ
x
+
(
1
?
θ
)
y
)
≤
θ
f
(
θ
)
+
(
1
?
θ
)
f
(
y
)
\forall x,y\in domf,0\leq\theta\leq1有 f(\theta x+(1-\theta)y)\leq \theta f(\theta)+(1-\theta)f(y)
?x,y∈domf,0≤θ≤1有f(θx+(1?θ)y)≤θf(θ)+(1?θ)f(y)
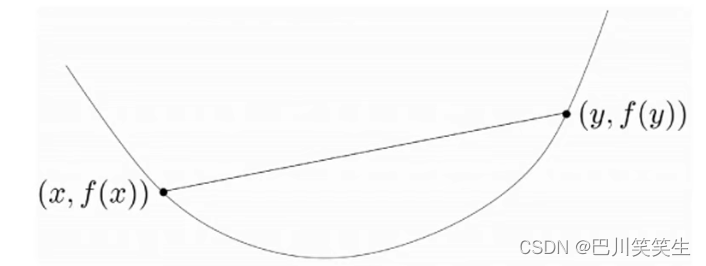
一阶可微
若
f
f
f一阶可微,则函数
f
f
f为凸函数当且仅当
f
f
f的定义域
d
o
m
f
dom f
domf为凸集且
?
x
,
y
∈
d
o
m
f
,
f
(
y
)
≥
f
(
x
)
+
▽
f
(
x
)
T
(
y
?
x
)
\forall x,y\in dom f,f(y)\geq f(x)+\bigtriangledown f(x)^{T}(y-x)
?x,y∈domf,f(y)≥f(x)+▽f(x)T(y?x)
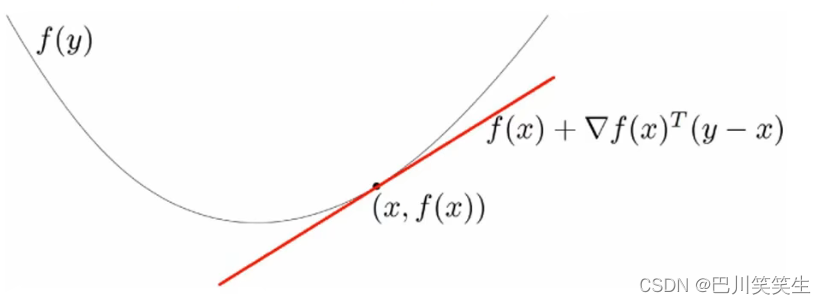
对于凸函数,其一阶泰勒近似本质为该函数全局估计
反之若一个函数一阶泰勒近似总是其全局下估计,则该函数为凸函数
二阶可微
若函数
f
f
f二阶可微,则函数
f
f
f为凸函数当且仅当
d
o
m
f
dom f
domf为凸集,且
▽
2
f
(
x
)
?
=
0
\bigtriangledown^{2}f(x)\succ =0
▽2f(x)?=0
若
f
f
f为一元函数,上式表示二阶导大于等于
0
0
0
若 f f f为多元函数,上式表示二阶导海森矩阵半正定
例子
- e a x e^{ax} eax
- x a , x ∈ R + , a ≥ 1 或 a ≤ 0 x^{a},x\in R_{+},a\geq1或a\leq 0 xa,x∈R+?,a≥1或a≤0
- ? l o g x -logx ?logx
- x l o g x xlogx xlogx
-
∣
∣
x
∣
∣
p
||x||_{p}
∣∣x∣∣p?
- m a x ( x 1 , . . . , x n ) max(x_{1},...,x_{n}) max(x1?,...,xn?)
- x 2 / a , a > 0 x^{2}/a,a>0 x2/a,a>0
- l o g ( e x 1 + . . . + e x n ) log(e^{x_{1}+...+e^{x_{n}}}) log(ex1?+...+exn?)
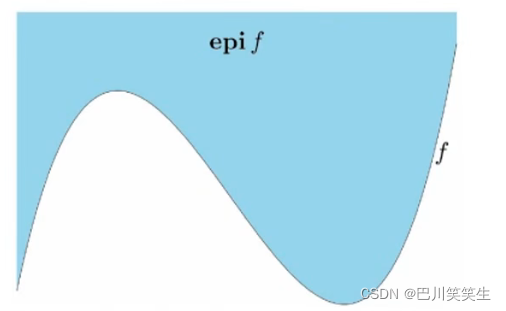
上境图
函数
f
f
f图像定义为
{
(
x
,
f
(
x
)
)
∣
x
∈
d
o
m
f
}
\{(x,f(x))|x\in dom f\}
{(x,f(x))∣x∈domf}
函数
f
f
f的上境图定义为
e
p
i
f
=
{
(
x
,
t
)
∣
x
∈
d
o
m
f
,
f
(
x
)
≤
t
}
epif=\{(x,t)|x\in domf,f(x)\leq t\}
epif={(x,t)∣x∈domf,f(x)≤t}
凸函数与凸集
一个函数是凸函数,当且仅当其上境图是凸集
一个函数为凹函数,当且仅当其亚图是凸集
h
y
p
o
f
=
{
(
x
,
t
)
∣
t
≤
f
(
x
)
}
hypo f=\{(x,t)|t\leq f(x)\}
hypof={(x,t)∣t≤f(x)}
杰森不等式
f
f
f是凸函数情况下
f
(
θ
x
+
(
1
?
θ
)
y
)
≤
θ
f
(
x
)
f(\theta x+(1-\theta)y)\leq\theta f(x)
f(θx+(1?θ)y)≤θf(x)
若
θ
1
.
.
.
θ
k
≥
0
,
θ
1
+
.
.
.
+
θ
k
=
1
则
f
(
θ
1
x
1
+
.
.
.
+
θ
k
x
k
)
≤
θ
1
f
(
x
1
)
+
.
.
.
+
θ
k
f
(
x
k
)
若\theta_{1}...\theta_{k}\geq 0,\theta_{1}+...+\theta_{k}=1\\ 则f(\theta_{1}x_{1}+...+\theta_{k}x_{k})\leq\theta_{1}f(x_{1})+...+\theta_{k}f(x_{k})
若θ1?...θk?≥0,θ1?+...+θk?=1则f(θ1?x1?+...+θk?xk?)≤θ1?f(x1?)+...+θk?f(xk?)
若
p
(
x
)
≥
0
在
S
?
d
o
m
f
,
∫
S
p
(
x
)
d
x
=
1
则
f
(
∫
S
p
(
x
)
x
d
x
)
≤
∫
S
f
(
x
)
p
(
x
)
d
x
或
f
(
E
x
)
≤
E
(
f
(
x
)
)
若p(x)\geq 0 在S\subseteq domf,\int_{S}p(x)dx=1 \\ 则f(\int_{S}p(x)xdx)\leq \int_{S}f(x)p(x)dx\\ 或f(Ex)\leq E(f(x))
若p(x)≥0在S?domf,∫S?p(x)dx=1则f(∫S?p(x)xdx)≤∫S?f(x)p(x)dx或f(Ex)≤E(f(x))
可由杰森不等式证明
D
(
p
∣
∣
q
)
=
∑
p
(
x
)
l
o
g
p
(
x
)
q
(
x
)
=
E
p
(
x
)
l
o
g
p
(
x
)
q
(
x
)
≥
0
D(p||q)=\sum p(x)log \frac{p(x)}{q(x)}=E_{p(x)}log\frac{p(x)}{q(x)}\geq 0
D(p∣∣q)=∑p(x)logq(x)p(x)?=Ep(x)?logq(x)p(x)?≥0
等等
保持函数凸性的算子
- 非负加权和
f ( x ) = w 1 f 1 ( x ) + . . . + w n f n ( x ) f(x)=w_{1}f_{1}(x)+...+w_{n}f_{n}(x) f(x)=w1?f1?(x)+...+wn?fn?(x) - 与仿射函数复合
g ( x ) = f ( A x + b ) g(x)=f(Ax+b) g(x)=f(Ax+b) - 逐点最大值,逐点上确界
f ( x ) = m a x ( f 1 ( x ) , . . . , f n ( x ) ) f ( x ) = sup ? y ∈ A g ( x , y ) f(x)=max(f_{1}(x),...,f_{n}(x))\\ f(x)=\sup_{y\in A}g(x,y) f(x)=max(f1?(x),...,fn?(x))f(x)=y∈Asup?g(x,y)
函数逐点上确界函数对应着函数上境图交集
凸优化
优化问题基本形式
最
小
化
f
0
(
x
)
,
x
∈
R
n
不
等
式
约
束
f
i
(
x
)
≤
0
,
i
=
1...
m
等
式
约
束
h
i
(
x
)
=
0
,
j
=
1...
p
无
约
束
优
化
m
=
p
=
0
最小化f_{0}(x),x\in R^{n}\\ 不等式约束f_{i}(x)\leq 0,i=1...m\\ 等式约束h_{i}(x)=0,j=1...p\\ 无约束优化m=p=0
最小化f0?(x),x∈Rn不等式约束fi?(x)≤0,i=1...m等式约束hi?(x)=0,j=1...p无约束优化m=p=0
优
化
问
题
的
域
D
=
?
i
=
1
m
d
o
m
f
i
∩
?
j
=
1
p
d
o
m
h
j
可
行
点
(
解
)
x
∈
D
且
满
足
约
束
条
件
可
行
域
,
所
有
可
行
点
集
合
优化问题的域D=\bigcap_{i=1}^{m} domf_{i} \cap \bigcap_{j=1}^{p}domh_{j} \\ 可行点(解)x\in D 且满足约束条件\\ 可行域,所有可行点集合
优化问题的域D=i=1?m?domfi?∩j=1?p?domhj?可行点(解)x∈D且满足约束条件可行域,所有可行点集合
最
优
化
值
p
?
=
i
n
f
{
f
0
(
x
)
∣
f
i
(
x
)
≤
0
,
i
=
1...
m
,
h
j
(
x
)
=
0
,
j
=
1...
p
}
最
优
化
解
p
?
=
f
0
(
x
?
)
最优化值p^{*}=inf\{f_{0}(x)|f_{i}(x)\leq0,i=1...m,h_{j}(x)=0,j=1...p\}\\ 最优化解p^{*}=f_{0}(x^{*})
最优化值p?=inf{f0?(x)∣fi?(x)≤0,i=1...m,hj?(x)=0,j=1...p}最优化解p?=f0?(x?)
凸优化问题基本形式
f
i
(
x
)
为
凸
函
数
h
j
(
x
)
为
仿
射
函
数
f_{i}(x)为凸函数\\ h_{j}(x)为仿射函数
fi?(x)为凸函数hj?(x)为仿射函数
重要性质
- 可行域为凸集
- 局部最优解为全局最优解
对偶问题
拉格朗日函数
L
(
x
,
λ
,
υ
)
=
f
0
(
x
)
+
∑
λ
i
f
i
(
x
)
+
∑
υ
j
h
j
(
x
)
L(x,\lambda,\upsilon)=f_{0}(x)+\sum \lambda_{i}f_{i}(x)+\sum\upsilon _{j}h_{j}(x)
L(x,λ,υ)=f0?(x)+∑λi?fi?(x)+∑υj?hj?(x)
对固定
x
x
x,拉格朗日函数
L
(
x
,
λ
,
υ
)
L(x,\lambda,\upsilon )
L(x,λ,υ)为关于
λ
\lambda
λ和
υ
\upsilon
υ的仿射函数
拉格朗日对偶函数
g
(
λ
,
υ
)
=
inf
?
x
∈
D
L
(
x
,
λ
,
υ
)
=
inf
?
x
∈
D
(
f
0
(
x
)
+
∑
λ
i
f
i
(
x
)
+
∑
υ
j
h
j
(
x
)
)
若
无
下
确
界
定
义
g
(
λ
,
υ
)
=
?
∞
g(\lambda,\upsilon)=\inf_{x\in D}L(x,\lambda,\upsilon)=\inf_{x\in D}(f_{0}(x)+\sum \lambda_{i}f_{i}(x)+\sum\upsilon _{j}h_{j}(x))\\ 若无下确界定义g(\lambda,\upsilon)=-\infty
g(λ,υ)=x∈Dinf?L(x,λ,υ)=x∈Dinf?(f0?(x)+∑λi?fi?(x)+∑υj?hj?(x))若无下确界定义g(λ,υ)=?∞
根据定义有:对
?
λ
≥
0
,
?
υ
\forall \lambda\geq 0,\forall\upsilon
?λ≥0,?υ,原优化问题有最优值
p
?
p^{*}
p?,则
g
(
λ
,
υ
)
≤
p
?
g(\lambda,\upsilon)\leq p^{*}
g(λ,υ)≤p?
进一步,拉格朗日对偶函数为凹函数
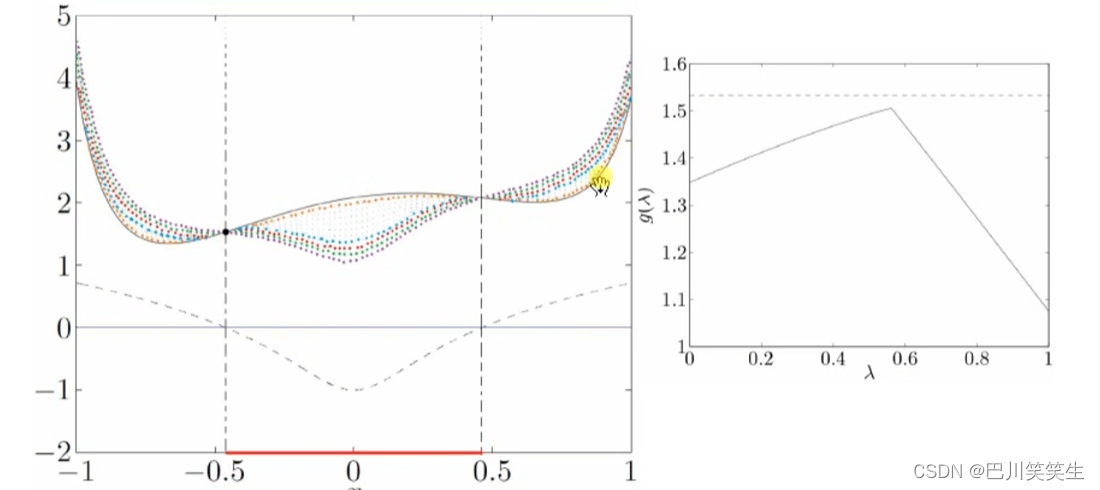
假设
x
0
x_{0}
x0?不可行,即存在
f
i
(
x
)
>
0
f_{i}(x)>0
fi?(x)>0,则选择
λ
i
→
∞
\lambda_{i}\rightarrow\infty
λi?→∞,对于其他乘子
λ
i
=
0
,
j
≠
i
\lambda_{i}=0,j\neq i
λi?=0,j?=i
假设
x
0
x_{0}
x0?可行,则有
f
i
(
x
)
≤
0
,
i
=
1...
m
f_{i}(x)\leq 0,i=1...m
fi?(x)≤0,i=1...m,令
λ
i
=
0
,
i
=
1...
m
\lambda_{i}=0,i=1...m
λi?=0,i=1...m
有
sup
?
λ
≥
0
L
(
x
,
λ
)
=
sup
?
λ
≥
0
(
f
0
(
x
)
+
∑
λ
i
f
i
(
x
)
)
=
{
f
0
(
x
)
,
f
i
(
x
)
<
0
∞
,
o
t
h
e
r
\sup_{\lambda\geq 0}L(x,\lambda)=\sup_{\lambda\geq 0}(f_{0}(x)+\sum\lambda_{i}f_{i}(x))= \left\{\begin{matrix} f_{0}(x),f_{i}(x)<0 \\ \infty,other \end{matrix}\right.
λ≥0sup?L(x,λ)=λ≥0sup?(f0?(x)+∑λi?fi?(x))={f0?(x),fi?(x)<0∞,other?
原问题为
inf
?
x
f
0
(
x
)
\inf_{x} f_{0}(x)
infx?f0?(x)转变为
inf
?
x
sup
?
λ
≥
0
L
(
x
,
λ
)
\inf_{x} \sup_{\lambda\geq 0}L(x,\lambda)
infx?supλ≥0?L(x,λ)
对偶问题是求对偶函数最大值,即
sup
?
λ
≥
0
inf
?
x
L
(
x
,
λ
)
\sup_{\lambda\geq0}\inf_{x}L(x,\lambda)
λ≥0sup?xinf?L(x,λ)
而
sup
?
λ
≥
0
inf
?
x
L
(
x
,
λ
)
≤
inf
?
x
sup
?
λ
≥
0
L
(
x
,
λ
)
\sup_{\lambda\geq0}\inf_{x}L(x,\lambda)\leq\inf_{x}\sup_{\lambda\geq0}L(x,\lambda)
λ≥0sup?xinf?L(x,λ)≤xinf?λ≥0sup?L(x,λ)
强对偶条件
对偶函数最大值为原问题最小值
f
0
(
x
?
)
=
g
(
λ
?
+
υ
?
)
=
inf
?
x
(
f
0
(
x
)
+
∑
λ
i
?
f
i
(
x
)
+
∑
υ
j
?
h
j
(
x
)
)
≤
f
0
(
x
?
)
+
∑
λ
i
?
f
i
(
x
x
)
+
∑
υ
j
?
h
j
(
x
?
)
≤
f
0
(
x
?
)
f_{0}(x^{*})=g(\lambda^{*}+\upsilon^{*})\\ =\inf_{x}(f_{0}(x)+\sum \lambda_{i}^{*}f_{i}(x)+\sum\upsilon _{j}^{*}h_{j}(x))\\ \leq f_{0}(x^{*})+\sum \lambda_{i}^{*}f_{i}(x^{x})+\sum\upsilon _{j}^{*}h_{j}(x^{*})\\ \leq f_{0}(x^{*})
f0?(x?)=g(λ?+υ?)=xinf?(f0?(x)+∑λi??fi?(x)+∑υj??hj?(x))≤f0?(x?)+∑λi??fi?(xx)+∑υj??hj?(x?)≤f0?(x?)
条件
f
i
(
x
?
)
≤
0
h
i
(
x
?
)
=
0
λ
i
?
≥
0
λ
i
?
f
i
(
x
?
)
=
0
i
=
1...
m
▽
f
0
(
x
?
)
+
∑
λ
i
?
▽
f
i
(
x
x
)
+
∑
υ
j
?
▽
h
j
(
x
?
)
=
0
f_{i}(x^{*})\leq 0\\ h_{i}(x^{*})= 0\\ \lambda_{i}^{*}\geq 0\\ \lambda_{i}^{*}f_{i}(x^{*})= 0\\ i=1...m\\ \bigtriangledown f_{0}(x^{*})+\sum \lambda_{i}^{*}\bigtriangledown f_{i}(x^{x})+\sum\upsilon _{j}^{*}\bigtriangledown h_{j}(x^{*})=0
fi?(x?)≤0hi?(x?)=0λi??≥0λi??fi?(x?)=0i=1...m▽f0?(x?)+∑λi??▽fi?(xx)+∑υj??▽hj?(x?)=0