题意:
有 N 种物品和一个容量是 V 的背包。第 i 种物品最多有 si 件,每件体积是 vi,价值是 wi。求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。输出最大价值。
分析:
这个问法还是典型的多重背包的问法,但是数据量就有点大了,单单靠朴素版的多重背包问题是解决不掉的。
数据范围
0<N≤1000
0<V≤20000
0<vi,wi,si≤20000
如果用朴素版的多重背包的话复杂度是O(nvs),是直接通不过。咱们现在可以先看一下朴素版的代码:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 1010,M = 20010;
int v[N],w[N],s[N];
int f[N][M];
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i]>>s[i];
for(int i=1;i<=n;i++){
for(int j=0;j<=m;j++){
f[i][j] = f[i-1][j];
for(int k=1;k<=s[i] && k*v[i] <= j;k++)
f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
}
}
cout<<f[n][m]<<endl;
return 0;
}
那现在咱们需要想一下别的办法了,请看图(注:以下的图均来自AcWing大佬彩色铅笔的博客)
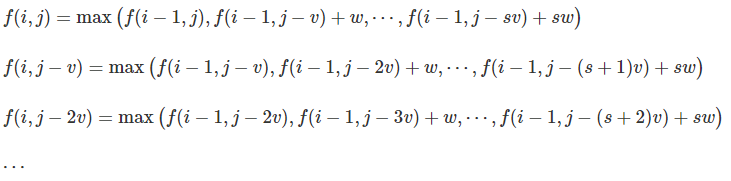
这是咱们当时做完全背包时推导出来的公式,但是多重背包和完全背包的最大的不同就是多重背包是有s这个上限的,所以说不能直接用f[i][j-v]这个来进行替代,咱们现在假设j%v = r,那么咱们就推导出了完整的方程组

我们现在把f(i-1,r)写成fr方便大家观看。

更直观点请看下图


于是通过枚举余数r,来对于每个r进行滑动窗口的优化,使得第三维是处于一个O(1)的状态,而且第i-1的状态可以记录下来,用一个滚动数组就很好用,就是再开一个数组g,每次更新f数组前都把f数组复制给g数组,现在具体请看代码:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int M = 20010;
int f[M],g[M];
int q[M];
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
int v,w,s;
cin>>v>>w>>s;
memcpy(g,f,sizeof f);
for(int r=0;r<v;r++){
int hh = 0,tt = -1;
for(int j=r;j<=m;j+=v){
if(hh <= tt && j-q[hh] > v*s) hh++;
while(hh <= tt && g[q[tt]] + (j-q[tt])/v*w <= g[j]) tt--;
q[++tt] = j;
f[j] = max(f[j],g[q[hh]] + (j-q[hh])/v*w);
}
}
}
cout<<f[m]<<endl;
return 0;
}