重温 dijkstra算法
Dijkstra算法 (迪杰斯特拉算法 ,卜老师纠正过是叫戴斯特比较标准)是典型最短路径算法,用于计算一个节点到其他节点的最短路径。
类似于广度优先搜索,它的主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
基本步骤 :
-
指定起点s;
-
定义一个数组dis表示s到每个点的距离,集合Q记录当前求出的最短路径点(距离起点)以及距离,一开始Q中只有s一个点且距离为0,而visited数组用于标记节点是否已经求出距离起点的最短距离;
-
找出Q的 当前求出的路径的最小值对于的节点,然后根据该节点的邻接点来更新dis以及更新Q。循环第三步 直到所有的节点都求出距离S的最短距离。
关键算法流程:
? 1. 首先构建节点的邻接表
2.优先队列用于储存当前已拓展节点构成的距离起点的距离队列 包含两个元素 (dis,node)dis表示起点到该node距离 ,将(0,s) 加入队列
? 3.队列元素不断弹出 ,每弹出一个没求出最小值的节点(visited标识)访问该节点的邻接表
? 对于该节点 tmp 的所有邻接点,计算若 起点 先走到tmp再到其邻接点的距离是否小于当前 dis表中节点到这些邻接点的距离,若小于则更新 ,且将(更新后的距离,节点序号 )加入到优先队列中
标识该节点tmp 已经求出最小值,之后若队列弹出tmp 不对其邻接点进行拓展
循环3
743. 网络延迟时间

? 对应题目 采用以上描述的方法
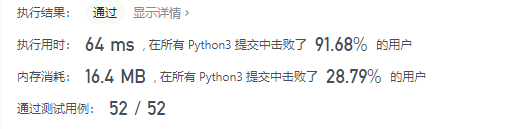
class Solution:
def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
k = k-1
dis = [9999]*n
vis = [0]*n
tgl = [[] for _ in range(n)]
for i,j,l in times:
tgl[i-1].append((j-1,l))
#tgl[j-1].append((i-1,l))
dis[k] = 0
heap = [(0,k)]
while heap:
d,tmp = heapq.heappop(heap)
if vis[tmp] ==0:
for j ,l in tgl[tmp]:
if dis[j]> dis[tmp]+l and vis[j]==0:
dis[j] = dis[tmp]+l
heapq.heappush(heap,(dis[j],j))
vis[tmp] =1
res =max(dis)
if res ==9999:
return -1
return res
1631. 最小体力消耗路径

?常规想到用队列来构建BFS算法, 逐一拓展 ,但是用dijkstra显然快很多, 对于这题就是一个二维的dijkstra ,整体代码 基本不变
、、
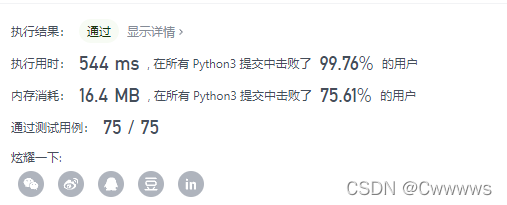
class Solution:
def minimumEffortPath(self, heights: List[List[int]]) -> int:
row,col = len(heights),len(heights[0])
heap= []
vis = [[0]*col for _ in range(row)]
ner = [[1,0],[-1,0],[0,1],[0,-1]]
heapq.heappush(heap,(0,0,0))
res = 0
while heap:
dis ,i,j = heapq.heappop(heap)
res =max(res,dis)
if i ==row-1 and j ==col-1:
return res
if vis[i][j] == 0:
for x,y in ner:
newi,newj = i+x,j+y
if 0<=newi<row and 0<=newj<col and vis[newi][newj]==0 :
newdis = abs(heights[i][j]-heights[newi][newj])
heapq.heappush(heap,(newdis,newi,newj))
vis[i][j]=1