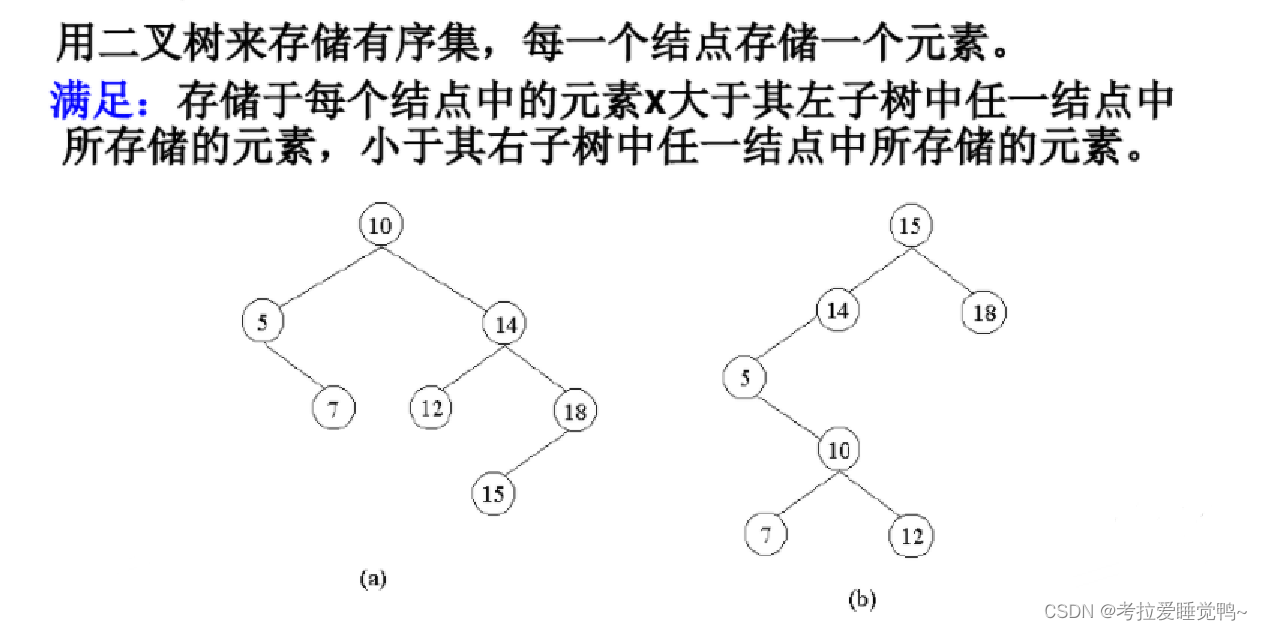
二叉搜索树基础
-
左边孩子节点的值 < 父节点的值?,右边孩子节点的值 > 父节点的值
-
每个二叉搜索树的子树也是一棵二叉搜索树
-
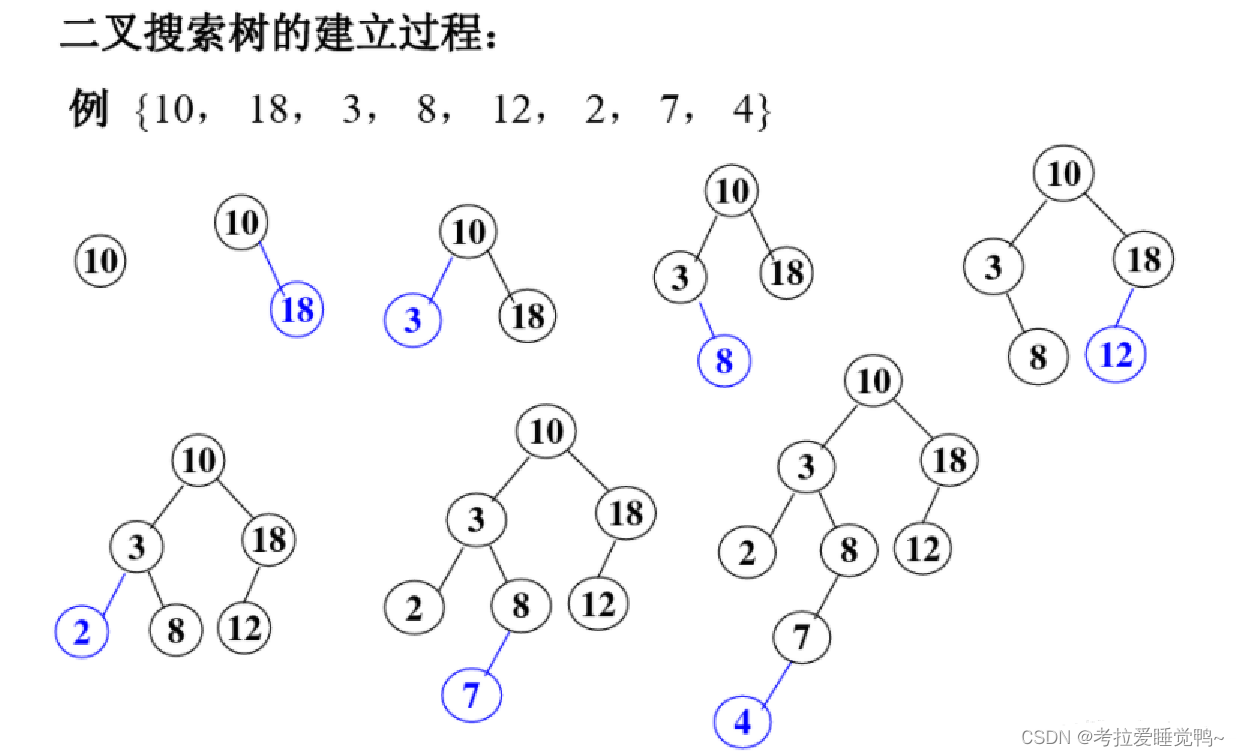
10 充当根节点
-
18 > 根节点,放在根节点右边;3 < 根节点,放在根节点左边;8 首先与根节点相比较,8 < 根节点,所以应该放在根节点的左边;然后 8 与 3 比较,3 < 8,8 应该放在 3 的右边,持续构建即可
-
二叉搜索树的特性:中序遍历是一个有序序列,从小到大排序,2-3-4-7-8-10-12-18
-
一般情况下数据没有重复的,每个节点都需要唯一的键,但是二叉搜索树可以存储任何类型·的数据 - - -> 为数据配建一个键即可
-
用递归法 || 非递归法遍历
-
一旦数据有序,创建出来的二叉搜索树就会出现不平衡的现象
?构建数据类型
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <string.h>
//二叉搜索树可以存储任何数据
typedef struct
{
int key; //键
char value[20]; //数据类型--->字符串类型
}DATA,*LPDATA;?树的节点结构体描述
typedef struct treeNode
{
DATA data; //数据
struct treeNode* LChild; //左子树指针
struct treeNode* RChild; //右子树指针
}NODE,*LPNODE;?创建节点 - - -> 把用户的数据变成一个节点
//传入数据
LPNODE createNode(DATA data)
{
LPNODE newNode = (LPNODE)malloc(sizeof(NODE)); //动态内存申请
assert(newNode);
//给数据做初始化
newNode->data = data;
newNode->LChild = NULL;
newNode->RChild = NULL;
return newNode;
}?二叉搜索树的结构体描述?- - -> 再封装的方式
typedef struct binarySearchTree
{
LPNODE root; //根节点
int treeSize; //树的当前元素个数
}BST,*LPBST;?创建二叉搜索树 - - -> 用结构体指针表示二叉搜索树
LPBST createBST()
{
LPBST tree = (LPBST)malloc(sizeof(BST)); //动态内存申请
assert(tree);
//描述二叉搜索树的最初状态
tree->root = NULL; //刚开始没有节点树为空
tree->treeSize = 0;
return tree;
}?万金油函数?
int size(LPBST tree)
{
return tree->treeSize;
}
int empty(LPBST tree) //如果树为空返回0 树不为空判断treeSize是否==0
{ //注意条件:树不能为空 为空不能判断NULL->treeSize
return tree==NULL?0:tree->treeSize == 0;
}?二叉搜索树的插入
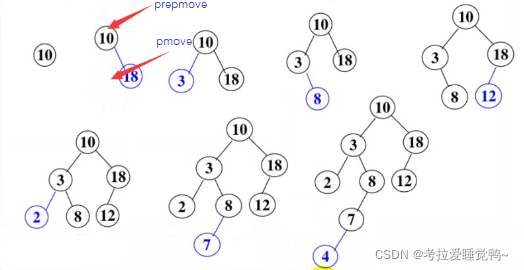
-
注意要记录移动节点的父节点的值prepmove:pmove的前驱节点
-
pmove走到空的位置才能做插入,插在移动的节点的父节点的左子树或者右子树的位置
-
怎么移动需要根据节点中的数据去做比较
//要插入的树 要插入的数据
void insertNode(LPBST tree, DATA data)
{
LPNODE newNode = createNode(data); //1.把用户的数据变成一个节点 2.找合适的位置
LPNODE pmove = tree->root; //定义一个移动的指针从根节点开始移动
LPNODE prepmove = NULL; //记录父节点的值
while (pmove != NULL) //根不等于空 做查找
{
prepmove = pmove; //记录前驱节点
if (pmove->data.key > data.key)//移动
{
pmove = pmove->LChild; //当前节点的数据>要插入数据的键 数据要往左边插
}
else if (pmove->data.key < data.key)
{
pmove = pmove->RChild; //当前节点的数据<要插入数据的键 数据要往右边插
}
else
{
//相等的键采用覆盖的方式
strcpy_s(pmove->data.value, 20, data.value);
return;
}
}
//移动节点的前驱节点prepmove 退出循环说明找到了合适的位置
//插在移动节点的左边还是右边需要分类讨论
if (tree->root == NULL) //树的根部==空,循环一次都没有执行
{
tree->root = newNode; //新的节点当作根节点
}
else //树!=空
{
//做插入讨论是插在 prepmove 的左边还是右边
if (prepmove->data.key > data.key)
{
prepmove->LChild = newNode;//当前节点的数据>要插入数据的键 数据要往左边插
}
else
{
prepmove->RChild = newNode;//当前节点的数据<要插入数据的键 数据要往右边插
}
}
tree->treeSize++; //当前元素个数++
}二叉搜索树的遍历?- - -> 递归法遍历
void printNode(LPNODE curNode)
{
printf("%d:%s\n", curNode->data.key, curNode->data.value); //打印数据
}
//要遍历的树
void midOrder(LPNODE tree)
{
if (tree != NULL)
{
midOrder(tree->LChild);
printNode(tree);
midOrder(tree->RChild);
}
}
//测试代码
int main()
{
LPBST tree = createBST(); //创建二叉搜索树
DATA data[8] = { 10,"张三",5,"李四",49,"王五",2,"小芳",
18,"小黑",89,"小红",0,"小明",22,"小花" };
for (int i = 0; i < 8; i++)
{
insertNode(tree, data[i]); //插入数据
}
midOrder(tree->root);
}
/*输出*/
0:小明
2:小芳
5:李四
10:张三
18:小黑
22:小花
49:王五
89:小红
二叉搜索树的查找 - - ->二分查找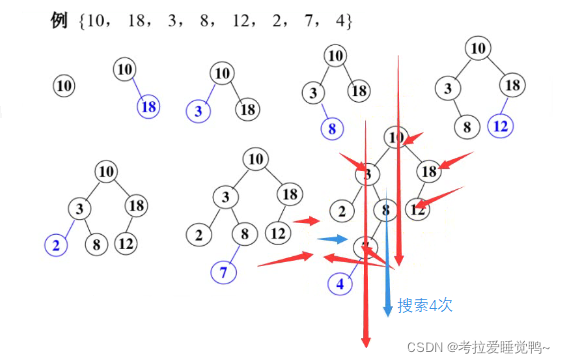
//二分查找 要搜索的树 通过键来搜索
LPNODE searchBST(LPBST tree, int key)
{
LPNODE pmove = tree->root; //定义一个移动的指针从根节点开始找
while (pmove != NULL && pmove->data.key != key) //pmove!=NULL&&data.key!=指定key
{
if (pmove->data.key > key)
{
pmove = pmove->LChild; //当前节点的数据>要插入数据的键 数据要往左边插
}
else
{
pmove = pmove->RChild; //当前节点的数据<要插入数据的键 数据要往右边插
}
}
return pmove; //返回空表示未找到 返回有用的节点--->找到了
}
//测试代码
LPNODE result = searchBST(tree,18);
printf("查找结果:");
printNode(result); //查找结果18:小黑二叉搜索树的删除
-
需要找删除的节点和删除节点的前驱节点(父节点)
-
注意两边都有节点的情况的处理:从左边拿节点或者从右边拿节点都可以
-
把两条边的情况变成一条边的情况
-
从左边拿节点:从删除节点的左子树中找最右边,如果最右边(当前节点)有左边就变成一条边的情况?- - ->?就是在剩下的子树中找一个最大的放上去
-
注意:删除 78 其实是需要删除两个节点,78 可以直接覆盖,对于 59,把 59 挪上去了,要对 59 再做一次删除,59 的删除是只有一条边的情况:只需要判断当前节点左边还是右边即可
-
从右边拿节点:从删除节点的右子树找最左边 - - -> 就是在剩下的子树中找一个最小的放上去
//要删除的树 通过键去做删除
void deleteNode(LPBST tree, int key)
{
//No.1 查找删除节点, 以及删除的节点父节点
LPNODE pmove = tree->root;
if (pmove == NULL)
{
printf("树为空,无法删除!");
return;
}
LPNODE pmoveparent = NULL;
while (pmove != NULL && pmove->data.key != key) //!=NULL&&!=指定key 让它们往下走
{
pmoveparent = pmove; //记录父节点
if (pmove->data.key > key)
{
pmove = pmove->LChild; //当前节点的数据>要插入数据的键 数据要往左边插
}
else if (pmove->data.key < key)
{
pmove = pmove->RChild; //当前节点的数据<要插入数据的键 数据要往右边插
}
else //两者相等直接退出循环
{
break;
}
}
//No.2
//2.1 分析查找结果,做不同的删除
if (pmove == NULL) //树为空无法删除
{
printf("没有找到指定位置无法删除\n");
return;
}
//2.2 左右子树都健全的情况--->需要把两条边的情况变成只有一条边的情况
if (pmove->LChild != NULL && pmove->RChild != NULL)
{
LPNODE moveNode = pmove->LChild; //从删除节点的左子树开始移动 要拿最右边
LPNODE moveNodeParent = pmove; //记录59的父节点
//走到左子树的最右边
while (moveNode->RChild != NULL) //不为空一直往右边走
{
moveNodeParent = moveNode; //记录父节点
moveNode = moveNode->RChild; //移动
}
//创建的节点要替换删除节点功能--->不是用直接修改数据的方式
//创建的节点数据是要调整的节点数据
//创建新节点59替换原来节点78的功能 78的左边连到59的左边、78的右边连到59的右边
LPNODE newNode = createNode(moveNode->data); //新节点的数据==原来的data
newNode->LChild = pmove->LChild; //新节点的左边==原来删除节点的左边
newNode->RChild = pmove->RChild; //新节点的右边==原来删除节点的右边
//分类讨论父节点是否存在,如果不存在说明删除节点是根节点
if (pmoveparent == NULL)
{
tree->root = newNode; //改变根节点的位置
}
else if (pmove == pmoveparent->LChild) //要删除的节点在原来父节点的左边
{
pmoveparent->LChild = newNode; //新节点成为原来父节点的左边
}
else
{
pmoveparent->RChild = newNode; //新节点成为原来父节点的右边
}
//为了删除调整的节点,适当调整一下指针的位置
if (moveNodeParent == pmove) //位置没有变化
{
pmoveparent = newNode;
}
else
{
pmoveparent = moveNodeParent;
}
free(pmove);
pmove = moveNode;
//依旧用pmove和pmoveparent来做调整节点的删除
}
//调整为只有一边的情况
LPNODE sNode = NULL;
if (pmove->LChild != NULL)
{
sNode = pmove->LChild; //!=NULL 存在左边记录要调整节点的左边
}
else
{
sNode = pmove->RChild; //pmove是要调整的节点,把要调整节点的孩子节点记录下来
}
if (tree->root == pmove) //判断根节点是否==要调整节点
{
tree->root = sNode;
}
else
{
if (pmove == pmoveparent->LChild)
{
pmoveparent->LChild = sNode; //放在调整的节点(父节点)的左边
}
else
{
pmoveparent->RChild = sNode;
}
}
free(pmove);
tree->treeSize--;
}
//测试代码
deleteNode(tree,49);
printf("\n删除后的结果!.....\n");
midOrder(tree->root);
/*输出*/
0:小明
2:小芳
5:李四
10:张三
18:小黑
22:小花
89:小红