题目概述(中等难度)
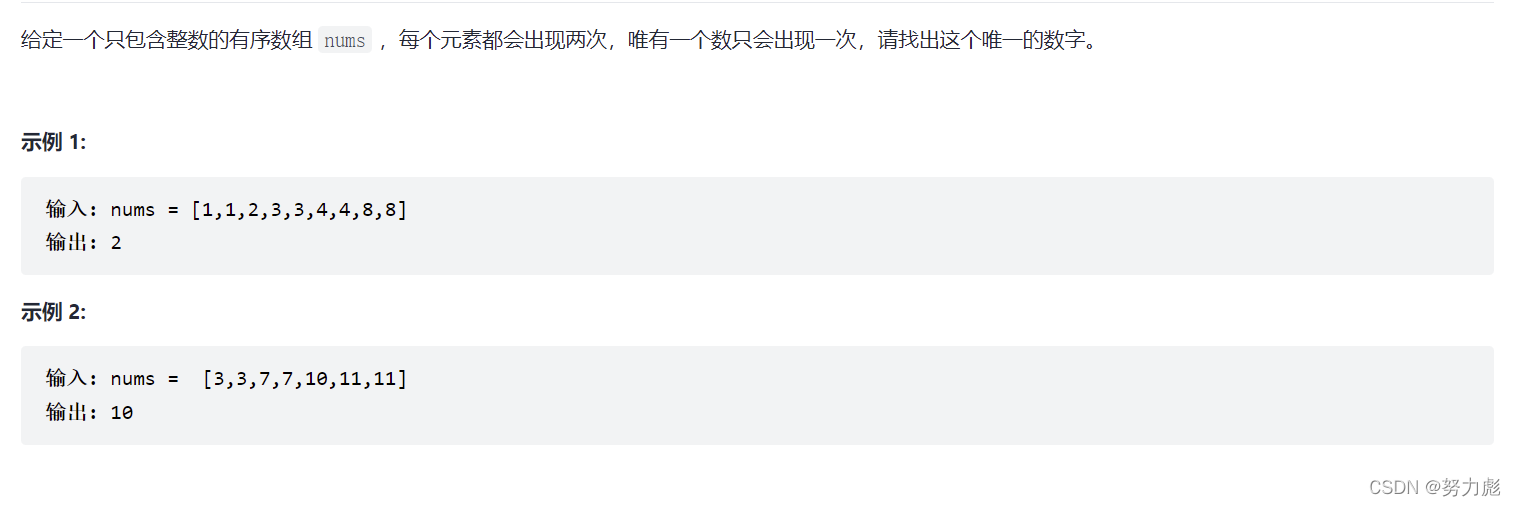
题目链接:
点我进入leetcode
思路与代码
思路展现
思路1 位运算(异或)
这个题目思路跟下面这个题目思路一摸一样,在这里不做过多赘述,我也就直接将博客链接放到这里:
点我进入博客
代码示例
class Solution {
public int singleNonDuplicate(int[] nums) {
int result = 0;
for(int i = 0; i < nums.length; i++) {
result ^= nums[i];
}
return result;
}
}
思路2 set集合
思路还是之前这道题目的思路,我吧博客链接放到这里:
点我进入博客
代码示例
class Solution {
public int singleNonDuplicate(int[] nums) {
HashSet<Integer> set = new HashSet<>();
set.add(nums[0]);
for(int i =1 ; i < nums.length ; i++) {
if(!set.contains(nums[i])) {
set.add(nums[i]);
}else {
set.remove(nums[i]);
}
}
for(Integer a : set) {
return a;
}
return 0;
}
}
思路3 二分法
二分法的思路是这样的:
因为数组中mid每次都是通过除以2来取到的,此时就会有奇数和偶数的区别,就会分为四种情况:
1:当我们mid是偶数的时候,说明此时下标为偶数,就与前面的数字进行判断,看是否相等,假设此时mid = 2,说明此时已经有三个数字了,当nums[mid] = nums[mid-1]的时候,说明此时前面三个数字中一定有一个数字出现了一次,那么就让 r = mid -1
2:当我们mid是偶数的时候,说明此时下标为偶数,就与前面的数字进行判断,看是否相等,假设此时mid = 2,说明此时已经有三个数字了,当nums[mid] != nums[mid-1]的时候,说明此时前面三个数字中一定是两个重复的数字,那么出现一次的数字一定在后面,那么就让 l = mid + 1
3:当我们mid是奇数的时候,说明此时下标为奇数,就与前面的数字进行判断,看是否相等,假设此时mid = 3,说明此时已经有四个数字了,当nums[mid] = nums[mid-1]的时候,说明此时前面四个数字中都是出现两次的数字,那么就让l = mid + 1
4:当我们mid是奇数的时候,说明此时下标为奇数,就与前面的数字进行判断,看是否相等,假设此时mid = 3,说明此时已经有四个数字了,当nums[mid] != nums[mid-1]的时候,说明此时前面四个数字中一定有一个数字出现了一次,那么就让 r = mid -1
于是乎便有了如下的代码:
代码示例
class Solution {
public int singleNonDuplicate(int[] nums) {
int n = nums.length;
if(n == 1){
return nums[0];
}
int l = 0, r = n-1;
//注意这块还是需要小于等于的
while(l <= r) {
int mid = (l + r)/ 2;
//找到首元素或者尾元素了,不用怀疑它就是那个唯一的元素
if(mid == 0 || mid == n-1) {
return nums[mid];
//四种情况分类讨论
}else if(mid % 2 == 0 && nums[mid] == nums[mid-1]) {
r = mid-1;
}
else if(mid % 2 == 1 && nums[mid] == nums[mid-1]) {
l = mid+1;
}
else if(mid % 2 == 0 && nums[mid] != nums[mid-1]) {
l = mid+1;
}
else if(mid % 2 == 1 && nums[mid] != nums[mid-1]) {
r = mid-1;
}
}
return nums[r];
}
}
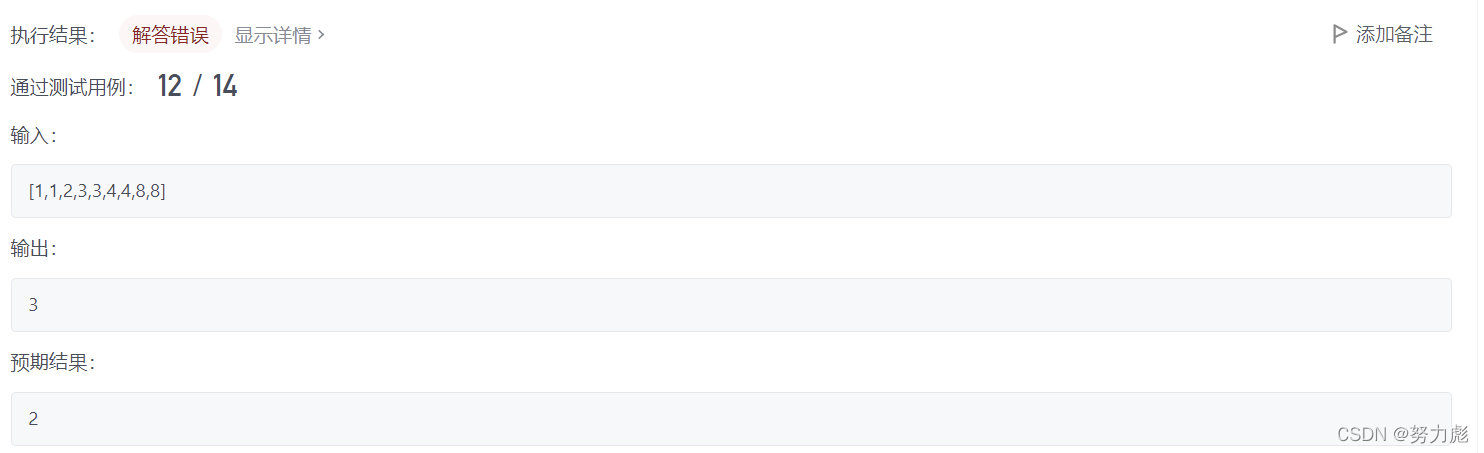
注意l还是需要小于等于的,不然下面的测试用例过不了: