法一:迭代
?参考代码:力扣
自己写的思路:
所谓中序遍历指的是,输出的时候是左子树,root,右子树。
所以先一直遍历左子树,把遍历的node都存入stack中;然后让栈顶节点出栈,出栈的同时,把它的右子节点压入栈,相当于递归右子节点。因为是中序遍历,在栈顶节点的右子节点压栈之前,要处理出栈节点的节点值,将它输出。
不同的子树要做同样的事情,一样要先将它的左子节点不断压栈,然后再出栈,带出右子节点入栈。
? 别人的思路:
中序遍历的迭代实现
搞清楚概念后,怎么用栈去模拟递归遍历,并且是中序遍历呢?
递归遍历一棵树,如下图,会先递归节点A,再递归B,再递归D,一个个压入递归栈。

即,先不断地将左节点压入栈,我们写出这部分代码:
while (root) {
? ? stack.push(root);
? ? root = root.left;
}
DFS的访问顺序是:根节点、左子树、右子树,现在要访问已入栈的节点的右子树了。
并且是先访问『位于树的底部的』即『位于栈的顶部的』节点的右子树。
于是,让栈顶节点出栈,出栈的同时,把它的右子节点压入栈,相当于递归右子节点。
因为是中序遍历,在栈顶节点的右子节点压栈之前,要处理出栈节点的节点值,将它输出。

新入栈的右子节点(右子树),就是在递归它。和节点A、B、D的压栈一样,它们都是子树。
不同的子树要做同样的事情,一样要先将它的左子节点不断压栈,然后再出栈,带出右子节点入栈。
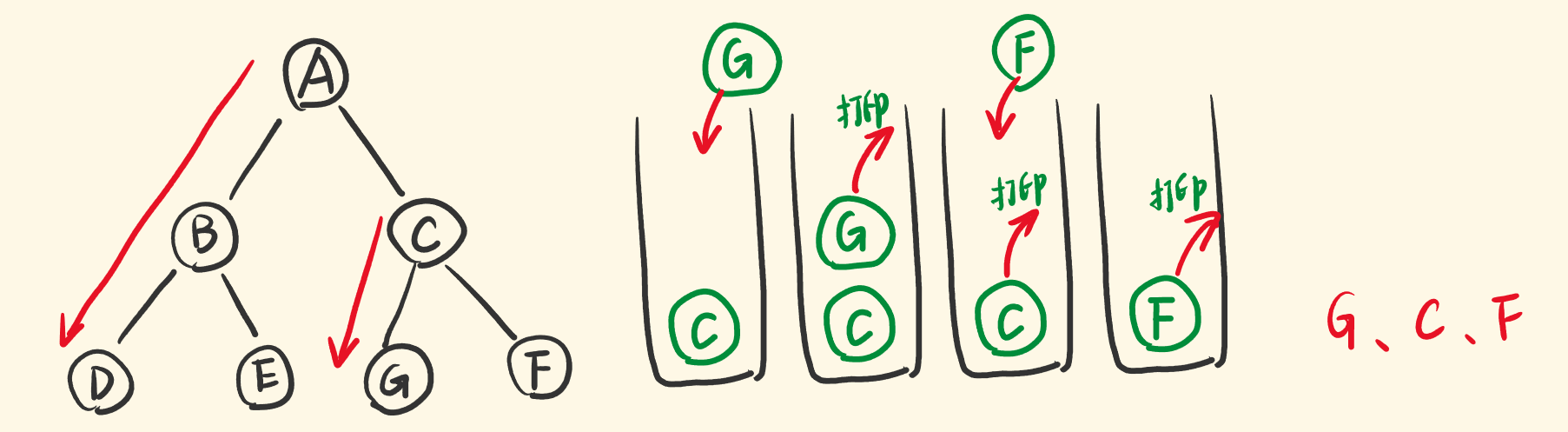
即栈顶出栈的过程,也要包含下面代码,可见下面代码重复了两次:
while (root) {
? ? stack.push(root);
? ? root = root.left;
}
其实这两个 while 循环,分别对应了下面的两次 inorder 调用,就是递归压栈:
inorder(root.left);
res.push(root.val);
inorder(root.right);自己默写的
func inorderTraversal(root *TreeNode) []int {
stack := []*TreeNode{}
res := []int{}
for root != nil {
stack = append(stack, root)
root = root.Left
}
for len(stack) != 0 {
node := stack[len(stack)-1]
stack = stack[0 : len(stack)-1]
res = append(res, node.Val)
node = node.Right
for node != nil {
stack = append(stack, node)
node = node.Left
}
}
return res
}抄袭的:
func inorderTraversal(root *TreeNode) []int {
res := []int{}
stack := []*TreeNode{}
for root != nil {
stack = append(stack, root)
root = root.Left
}
for len(stack) != 0 {
node := stack[len(stack)-1]
stack = stack[:len(stack)-1]
res = append(res, node.Val)
node = node.Right
for node != nil {
stack = append(stack, node)
node = node.Left
}
}
return res
}
法二:递归
参考链接:力扣
递归就是一种循环,一种自己调用自己的循环。
一道题你看能不能用递归实现,需要具备两个条件:
- 问题可以分为多个重复的子问题,子问题仅存在数据规模的差距。
- 存在终止条件。
所以根据条件,对于实现递归,只需要两步:
- 找出重复的子问题(递推公式)。
- 终止条件。
根据上面讲的实现递归的两步来找:
(1) 找出重复的子问题
中序遍历的顺序是:左子树、根、右子树。
对于左子树、右子树来说,也是同样的遍历顺序。
所以这个重复的子问题就是:先遍历左子树、再取根节点,最后遍历右子树。
inOrder(root.left)
print(root.val)
inOrder(root.right)
(2) 确定终止条件
和前序遍历相同,就是当前的节点为空,空的没啥好遍历的。
if root == None:
? ? return?
最重要的两点确定完了,那总的代码也就出来了。
func inorderTraversal(root *TreeNode) []int {
res := []int{}
inorder(root, &res)
return res
}
func recursion(root *TreeNode, resource *[]int) {
if root == nil {
return
}
recursion(root.Left, resource)
*resource = append(*resource, root.Val)
recursion(root.Right, resource)
}总程序:
package main // 声明 main 包,表明当前是一个可执行程序
//https://blog.csdn.net/u013837825/article/details/120857910
//https://leetcode-cn.com/problems/binary-tree-inorder-traversal/solution/shou-hua-tu-jie-yong-zhan-mo-ni-zhong-xu-bian-li-z/
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
func inorderTraversal(root *TreeNode) []int {
stack := []*TreeNode{}
res := []int{}
for root != nil {
stack = append(stack, root)
root = root.Left
}
for len(stack) != 0 {
node := stack[len(stack)-1]
stack = stack[0 : len(stack)-1]
res = append(res, node.Val)
node = node.Right
for node != nil {
stack = append(stack, node)
node = node.Left
}
}
return res
}
func inorderTraversal_recursion(root *TreeNode) []int {
res := []int{}
recursion(root, &res)
return res
}
func recursion(root *TreeNode, resource *[]int) {
if root == nil {
return
}
recursion(root.Left, resource)
*resource = append(*resource, root.Val)
recursion(root.Right, resource)
}
func addNode(head *TreeNode, value int) *TreeNode {
if head == nil {
return &TreeNode{value, nil, nil}
} else if value >= head.Val {
head.Right = addNode(head.Right, value)
} else {
head.Left = addNode(head.Left, value)
}
return head
}
func main() { // main函数,是程序执行的入口
root := TreeNode{Val: 1}
root.Left = &TreeNode{Val: 2}
root.Right = &TreeNode{Val: 3}
root.Left.Left = &TreeNode{Val: 4}
root.Left.Right = &TreeNode{Val: 5}
root.Right.Left = &TreeNode{Val: 6}
root.Right.Right = &TreeNode{Val: 7}
root.Left.Left.Left = &TreeNode{Val: 8}
root.Left.Right.Right = &TreeNode{Val: 9}
root.Right.Right.Right = &TreeNode{Val: 10}
//root := addNode(nil, 1)
//addNode(root, 1)
//addNode(root, 7)
//addNode(root, 2)
//addNode(root, 6)
//addNode(root, 5)
//addNode(root, 3)
res := inorderTraversal_recursion(&root)
println(res)
}
?自己默写的,没有提示,纯手工:
func inorderTraversal(root *TreeNode) []int {
stack := []*TreeNode{}
res := []int{}
for root!=nil {
stack = append(stack,root)
root = root.left
}
for len(stack)>0 {
node := stack[len(stack)-1]
res = append(res,node.value)
stack = stack[0:len(stack)-1]
root = node.right
for root!=nil {
stack = append(stack,root)
root = root.left
}
}
return res
}