[数据结构与算法]差分约束原理 例题：区间

差分约束是用最短路算法解决两种问题

1.求不等式组可行解

2.求可行解中所有解最大值或最小值

2.有两种意思，总共的最值和单个解的最值。在差分约数问题中单个最优就能导出全局最优，下面会证明。

差分约束能解决如下形如下方的不等式组

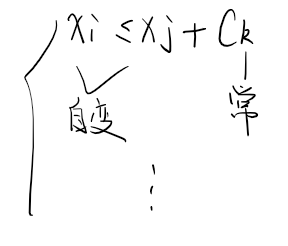
形式全部都是xi <= xj + ck的形式（或 >=)

对于一个已经计算好最短路的图，满足三角不等式，如下有对应关系

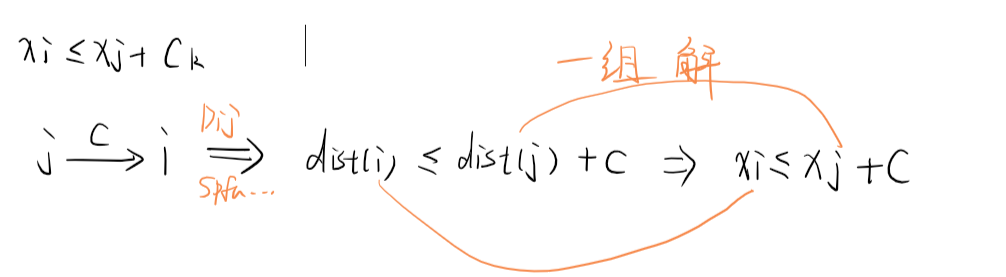
建立变量和点的对应关系，到一个点的最短距离就是一个变量的可行解。

求不等式组可行解需要满足条件 ：源点要满足从源点出发，一定可以走到到所有的边 （有孤立点，则孤立点可以取任意值，无限制）

如果有负环则不等式矛盾无解，证明如下

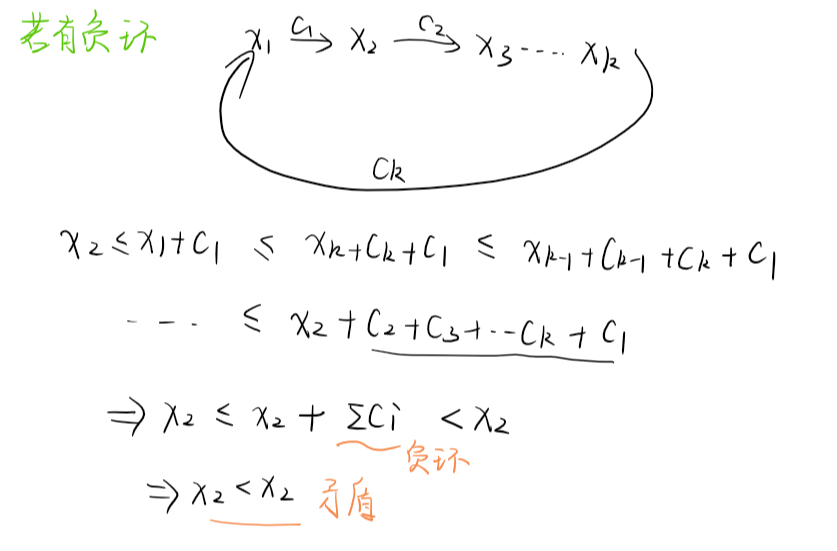
求最大值或最小值,这里最值是每个变量的最大值/最小值

结论：求最大是求最短路，求最小最长路

/*
 * @Author: 爱学习的图灵机
 * @Date: 2022-02-22 22:13:39
 * @LastEditTime: 2022-02-27 16:29:39
 * Bilibili:https://space.bilibili.com/7469540
 * 题目地址:https://www.acwing.com/activity/content/problem/content/1534/
 * @keywords: 差分约束
 */

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 50010, M = 150010;

int n;
int h[N], e[M], w[M], ne[M], idx;
int dist[N];
int q[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

void spfa()
{
    memset(dist, -0x3f, sizeof dist);
    dist[0] = 0;
    st[0] = true;
    int hh = 0, tt = 1;
    q[0] = 0;

    while (hh != tt)
    {
        int t = q[hh ++ ];
        if (hh == N) hh = 0;
        st[t] = false;

        for (int i = h[t]; ~i; i = ne[i])
        {
            int j = e[i];
            if (dist[j] < dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                if (!st[j])
                {
                    q[tt ++ ] = j;
                    if (tt == N) tt = 0;
                    st[j] = true;
                }
            }
        }
    }
}

int main()
{
    scanf("%d", &n);

    memset(h, -1, sizeof h);
    for (int i = 1; i < N; i ++ ) // 到N，答案要输出d[50001]
    {
        add(i - 1, i, 0);
        add(i, i - 1, -1);
    }

    for (int i = 0; i < n; i ++ )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        a ++, b ++ ;
        add(a - 1, b, c);
    }

    spfa();

    printf("%d\n", dist[50001]);

    return 0;
}