蝙蝠算法

蝙蝠的生物习性

在这里插入图片描述
蝙蝠的回声定位：蝙蝠通过发射非常响亮的声音脉冲并倾听周围物体发出的回声，以此来确定猎物的大小和自己与猎物之间的距离，来决定自己说加速/减速并向着猎物/远离猎物飞行。蝙蝠发出的脉冲具有回声频率和回声响度，回声频率与相对距离决定蝙蝠的速度，而速度与当前位置决定了蝙蝠下一刻的位置。回声频率会随着接近猎物而逐渐增大（因为需要更快确定猎物的位置），回声响度会随着接近猎物而逐渐减小（为了防止吓到猎物）。

事实上，蝙蝠的回声定位是一种非常复杂的机制，这里并没有完全按照其捕猎机制来模拟算法，而是精简出来其中的回声频率和回声响度两个主要属性。

近似化规则

为简单起见，我们现在使用以下近似的或理想化的规则：

每只蝙蝠都使用回声定位系统来测量猎物对周围环境的距离。
蝙蝠在位置xi以速度vi自发飞行，回声频率范围fi为[fmin,fmax]的一个随机数，波长λ和响度Ao随着迭代进行改变以寻找猎物（即最优解）。
随着靠近猎物，脉冲发射的回声频率r增加，回声响度A会降低。
响度A的取值范围为[Amin,A0]。随着迭代由A0逐渐减小为Amin。

算法参数

蝙蝠算法的参数

N:蝙蝠的数量。
fmin、fmax ：蝙蝠的最大和最小频率，确定最佳蝙蝠位置的共享率，也就是当前最佳对别的蝙蝠的影响大小。
vi：蝙蝠i的速度，从0开始并随着迭代更新。
Aj：响度，有助于更新蝙蝠的位置，从1到0随着迭代而减小，因为蝙蝠越靠近猎物（最优点）响度越低。初始值为1.
rj：脉冲频率，控制算法的全局搜索。rj的初始值为0.01
α, γ : 这是两个[0,1]之间的数，用于控制Aj和rj随着迭代而减小与增大。
ε：这是[-1,1]之间的数，以确定在全局搜索中梯度的大小。
因此A->0,r->∞当迭代次数足够大的时候。

算法流程与步骤

步骤1：初始化算法参数。

f(x) x ∈ [LB,UB]（d维度下），其中f(x)是适应度函数，x为蝙蝠位置的d维矢量，LB、UB分别是下界和下界，同时也要初始化N，fmin、fmax，vi，Aj，rj，α, γ，ε。

步骤2：初始化蝙蝠的解空间。

BM是一个大小为N×d的增广矩阵（N行，每行即为一个蝙蝠及其坐标；d列意思是问题是d维问题，坐标有d个维度的）。
N个蝙蝠都位置向量随机公式生成如下：

x^j_i = LB_i +（ UB_i ? LB_i ）× U（0,1）

其中?i=1,2，…，d并且?j=1,2，…，N 。而U（0,1）是0到1之间的随机数。生成的解根据其目标函数值存储在BM中，其中f(x¹)≤f(x²)≤……≤f(x^N)。
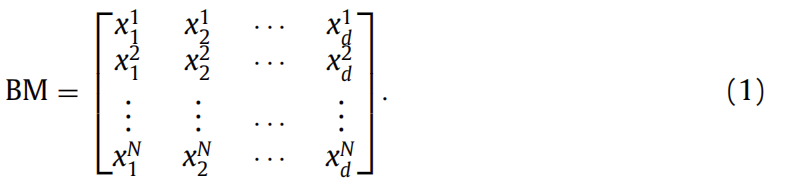在这里插入图片描述需要注意的是，最佳蝙蝠位置xGbest在这一步中初始化为x^Gbest=x¹。

步骤3：蝙蝠解空间的局部搜索

在这一步中，每个蝙蝠xj飞行的速度vj受到一个随机产生的频率fj的影响。然后将搜索空间中的新蝙蝠位置x’^j更新如下：
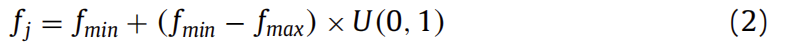
在这里插入图片描述
其中，?i=1,2，…，d和?j=1,2，…，n。
注意，这一步被称为局部搜索，是因为更新的蝙蝠新位置是基于之前的蝙蝠位置，在之前的位置上添加了一个相对较小的值，这个小值是受f与之前的位置到当前全球最佳x^Gbest共同影响的。因此新的位置是在之前位置上的局部随机搜索，并且有对当前全球最佳x^Gbest的倾向。

但是我并不清楚为什么会是x^j_i-x^Gbest而不是x^Gbest-x^j_i，因为前一个是远离全球最佳，而后一个是接近全球最佳。

步骤4：蝙蝠解空间的最优局部搜索

以rj的概率进行新的局部搜索，直接跳到最佳解的附近位置进行随机游走
在这里插入图片描述但论文中却说这是一种全局搜索，在详细解释中又说这是一种局部搜索，其实我更倾向于这就是一种局部的搜索，因为他依然是在最优解附近生成一个新的解。

第三步与第四步可以总结为以下公式：
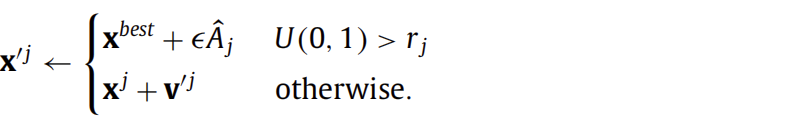在这里插入图片描述也就是以ri的概率跳到最佳的附近游走，否则就在自己的附近游走

步骤5：更新蝙蝠种群的位置
对于BM中的每只蝙蝠，新的蝙蝠位置只有在满足以下两个条件的时候才会进行更新。
①U(0, 1) < A_j
②f(x '^j) < f(x^j)
也就是当新的解更优的情况下才有Aj的概率更新位置，并且这个概率A_j会随着迭代越来越低，越到后面越难更新，即使更优也依然不更新，这是难以理解的地方，但是本人更改了代码为只要更优则更新得到的解之后得到的答案并没有变得更好。

步骤6：停止迭代。
终止标准通常与计算时间限制、数量或最大迭代次数或最终结果的质量有关。

蝙蝠算法的流程图

在这里插入图片描述

蝙蝠算法的伪代码

在这里插入图片描述

算法应用

f(x)=z=sum((x-2).^2)，求f(x)min。

以下是Dr.Yang的代码

% ----------------------------------------------------------------------- %
% The bat algorithm (BA) for continuous function optimization (demo)      %
% Programmed by Xin-She Yang @Cambridge University 2010                   %
% ----------------------------------------------------------------------- %

% References: ----------------------------------------------------------- %
% 1) Yang X.S. (2010). A New Metaheuristic Bat-Inspired Algorithm, In:    %
%   Nature-Inspired Cooperative Strategies for Optimization (NICSO 2010), %
%   Studies in Computational Intelligence, vol 284. Springer, Berlin.     %
%   https://doi.org/10.1007/978-3-642-12538-6_6                           %
% 2) Yang X.S. (2014). Nature-Inspired Optimization Algorithms, Elsevier. %
% ----------------------------------------------------------------------- %

function [best,fmin,N_iter]=bat_algorithm_new(inp)
if nargin<1,
   inp=[20 1000];    % Default values for n=10 and t_max=1000
end
% Initialize all the default parameters
n=inp(1);       % Population size, typically 20 to 40 
t_max=inp(2);   % Maximum number of iterations
A=1;            % Initial loudness (constant or decreasing)
r0=1;           % The initial pulse rate (constant or decreasing)
alpha=0.97;     % Parameter alpha
gamma=0.1;      % Parameter gamma
% Frequency range
Freq_min=0;     % Frequency minimum
Freq_max=2;     % Frequency maximum
t=0;            % Initialize iteration counter
% Dimensions of the search variables
d=10;          
% Initialization of all the arrays
Freq=zeros(n,1);   % Frequency-tuning array
v=zeros(n,d);      % Equivalnet velocities or increments
Lb=-5*ones(1,d);   % Lower bounds
Ub=5*ones(1,d);    % Upper bounds
% Initialize the population/solutions
for i=1:n,
  Sol(i,:)=Lb+(Ub-Lb).*rand(1,d);
  Fitness(i)=Fun(Sol(i,:));
end
% Find the best solution of the initial population
[fmin,I]=min(Fitness);
best=Sol(I,:);

% Start the iterations -- the Bat Algorithm (BA) -- main loop
while (t<t_max)
   % Varying loundness (A) and pulse emission rate (r)
   r=r0*(1-exp(-gamma*t));
   A=alpha*A;
   % Loop over all bats/solutions
   for i=1:n,
       Freq(i)=Freq_min+(Freq_max-Freq_min)*rand;
       v(i,:)=v(i,:)+(Sol(i,:)-best)*Freq(i);
       S(i,:)=Sol(i,:)+v(i,:);
   % Check a switching condition
   if rand<r,
       S(i,:)=best+0.1*randn(1,d)*A;
   end

   % Check if the new solution is within the simple bounds
   S(i,:)=simplebounds(S(i,:),Lb,Ub);
   % Evaluate new solutions
   Fnew=Fun(S(i,:));
   % If the solution improves or not too loudness
    if ((Fnew<=Fitness(i)) & (rand>A)),
       Sol(i,:)=S(i,:);
       Fitness(i)=Fnew;
    end
   % Update the current best solution
    if Fnew<=fmin,
       best=S(i,:);
       fmin=Fnew;
    end
   end % end of for i
  t=t+1;  % Update iteration counter
  % Display the results every 100 iterations
  if ~mod(t,100),
     disp(strcat('Iteration = ',num2str(t)));    
     best, fmin 
  end
end  % End of the main loop

% Output the best solution
disp(['Best =',num2str(best),' fmin=',num2str(fmin)]);

% Application of simple bounds/constraints
function s=simplebounds(s,Lb,Ub)
  % Apply the lower bound
  ns_tmp=s;
  I=ns_tmp<Lb;
  ns_tmp(I)=Lb(I);
  
  % Apply the upper bounds 
  J=ns_tmp>Ub;
  ns_tmp(J)=Ub(J);
  % Update this new move 
  s=ns_tmp;

% The cost function or objective function
function z=Fun(x)
z=sum((x-2).^2);      % Optimal solution fmin=0 at (2,2,...,2)

性能评价

由以上具体的步骤就可以看出，蝙蝠算法非常集中于局部最优解的搜寻，几乎没有全局搜索，所以非常容易陷入局部最优难以跳出但是优点就是收敛速度快。并且有着非常难以理解的三点，一是向着最优的反方向进行随机游走，二是即使新的解更优也不一定接受新的解还必须满足rand>A，三是我找到的所有版本的BA算法的代码中的注释都有着这样一句话 % If the solution improves or not too loudness但是下面的代码却是if ((Fnew<=Fitness(i)) & (rand>A)),难道这里不是and吗?

总的来说，蝙蝠算法有很多不理解的地方，感觉在算法设计上也和蝙蝠的实际回声搜索差别很大，效果也不是那么好，是一个学的不太好的算法。