求凹多边形内角

我们常见的多边形多为凸多边形，即其每个内角θ小于180°的多边形。而凹多边形的一些内角θ大于180°。在Matlab求多边形内角时，通常已知条件是多边形所有顶点的坐标。若是一般的凸多边形，我们可以使用相邻三点的坐标，将其视为三角形的三个顶点，求出两边夹角，即多边形顶点的内角。公式如下：
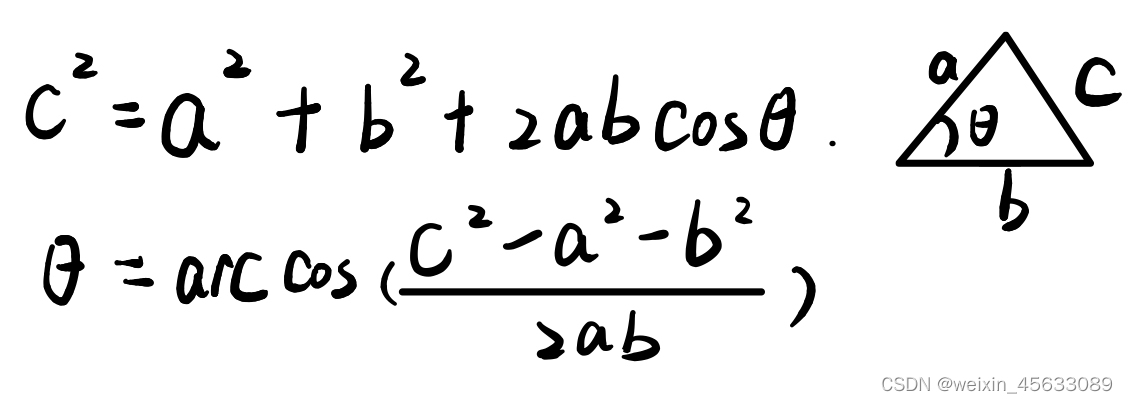
请添加图片描述
或者将这三点视为两条向量，通过点积与范数来计算向量之间的夹角。公式如下：

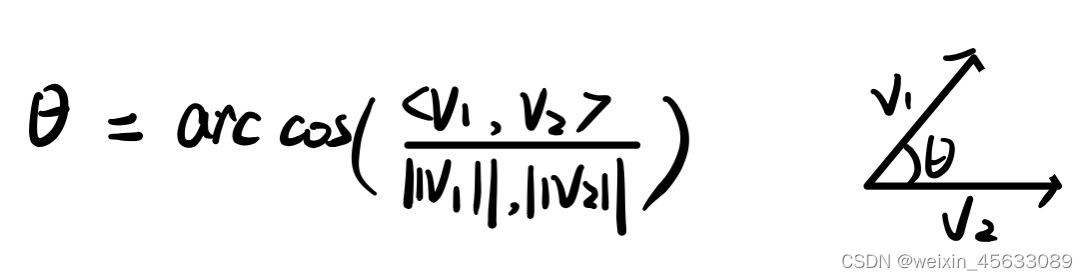
使用手算时，对于凹多边形的内角，只需找到相应的内角，使用 360°-θ即可。然而，Matlab在用以上公式进行计算时，并不能识别出哪个内角是凹或凸，计算出来的结果都是凸的内角，小于180°。因此，需要通过其他功能函数先判断内角的凹凸性质，才能正确计算出凹多边形的内角。
Matlab社区里面已经有大佬Are Mjaavatten将判断内角凹凸性质写成一个功能函数：convex，可以在matlab官网上登录后直接下载下来调用。
在Matlab社区File Exchange内可以搜索到许多大佬贡献的优秀功能函数，推荐在里面找到一些便利的扩展函数。

% ps包含着多边形的坐标的nx2矩阵
c = convex(ps); % convex函数是判断对应顶点内角是否大于180°
for k = 1 : size(ps, 1)-2
    point1 = ps(k, :);
    vertex = ps(k+1, :);
    point2 = ps(k+2, :);
    v1 = point1 - vertex;
    v2 = point2 - vertex;   
    % 使用点积与范数求角度，需要用c值判断内角是否大于180°
    theta(k) = dot(v1, v2)/(norm(v1)*norm(v2));  % dot点积函数，norm范数取模函数
    if c(k)>0  
        angle(k) = (acos(theta(k)))*180/pi;
    else
        angle(k) = 360 - (acos(theta(k)))*180/pi;
    end
end