[数据结构与算法]【计算机网络】第三部分 数据链路层(10) 检错与纠错

网络必须能够以可接受的准确率将数据从一个设备传送到另一个设备。对于大多数应用，系统必须保证接收到的数据与发送的数据是一致的。将数据从一个节点传送到下一个节点的过程中，数据有可能遭到破坏，因为有许多因素影响或改变一个数据报文的一位或多位。有些应用要求有一个机制，用以检测或纠正这些差错 error ——有些应用能忍受一些小差错。比如，可以忍受音频或视频传输中的随机差错，但是传输文本时，期望得到很高的准确率。

10.1 引言

首先直接地或间接地讨论，有关差错检测和差错纠正的问题。

10.1.1 差错的类型

无论何时，在位流从一点流动到另一点时，由于干扰 interference 的存在，都可能经受到不可预测的变化，这些干扰可能会改变信号的波形。在单个位差错中，就是由 $0$ 变成 $1$ 或是由 $1$ 变成 $0$ 。在突发性差错中，可能有多个位的改变。例如，在一个具有 $1200\text{bps}$ 速率的传输中，一个 $0.01s$ 的脉冲噪声突发，可能要改变 $12$ 位信息中一些位或所有位。

1. 单个位差错

单个位差错 single-bit error 一词的意思是，在给定的数据单元（例如一个字节、字符或分组）中仅有一位发生从 $1$ 到 $0$ 或从 $0$ 到 $1$ 的变化。

图10.1说明在一个数据单元中单个位差错的影响。为了理解这一变化的影响，设想每一个 $8$ 位组是一个左边加一个 $0$ 位的ASCII码字符。在图10.1中，发送 $00000010$（ASCII的 STX ) ，表示文本的开始，但是接收方接收的是 $00001010$（ASCII的 LF ) ，表示换行。

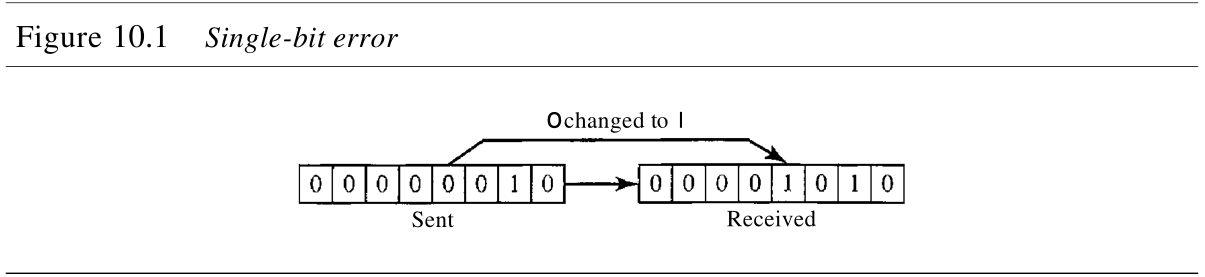
单个位差错在串行数据传输中很少出现。要了解为什么，可以想像以 $1\text{Mbps}$ 发送数据的情况。这意味着每一位仅持续 $1/1000000s$ 即 $1\mu s$ 。要出现单个位差错，噪音信号必须只有 $1\mu s$ 的持续时间，而这是非常罕见的情况，一般的噪音信号都比这个时间要长。

2. 突发性差错

突发性差错 burst error 是指在数据单元中有两位或更多位发生 $1$ 到 $0$ 或 $0$ 到 $1$ 的变化。

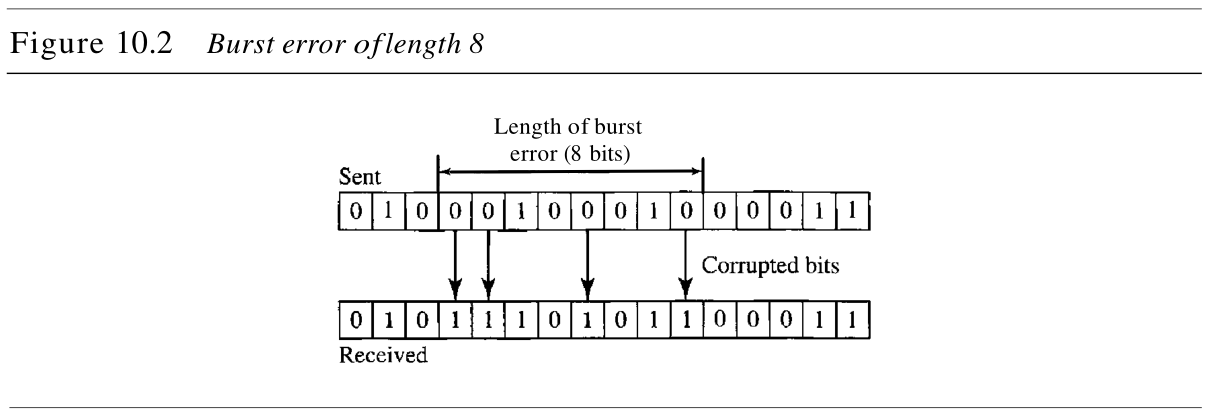
图10.2说明在数据单元中的一个突发性差错的影响。在这种情况下，发送的是 $0100010001000011$ ，但是接收的却是 $0101110101100011$ 。注意：突发性差错并不意味着差错在连续位上出现。突发性差错的长度按从第一个差错位到最后一个差错位的长度计算，其间的某些位也可能未产生差错。

突发性差错比单个位差错更容易发生。噪声的持续时间要大于一个位的持续时间，这就意味着在噪声影响数据时，它要影响许多位。受影响的位的数量取决于数据速率和噪声的持续时间。例如，如果以 $1\text{Kbps}$ 的速率发送数据，一个 $1/100s$ 的噪声就会影响 $10$ 位；而如果我们以 $1\text{Mbps}$ 的速率发送数据，同样的噪声就会影响 $10000$ 位。

10.1.2 冗余

检错或纠错的核心概念是冗余 redundancy 。为了能检测或纠正差错，我们除了数据外，还需要发送一些额外的位。这些冗余位由发送方添加、并由接收方除去。它们的存在允许接收方检测或纠正被破坏的位。

10.1.3 检错和纠错

差错的纠正比检测更难。在检错 error detection 中，只看是否发生差错。回答是简单的是或否，甚至对差错个数都不感兴趣。对我们来说，单个位差错和突发性差错是一样的。

在纠错 error correction 中，需要知道被破坏的位的个数，更重要的是知道它们在报文中的位置。差错个数和报文长度是重要的因素。如果需要纠正 $8$ 位数据单元中的单个位差错，则需要考虑 $8$ 个可能的差错位置。如果需要纠正相同长度数据单元中的两个差错，则需要考虑 $28$ 种可能。可以想像，要在 $1000$ 位数据单元中查找 $10$ 个差错，是多么难了。

10.1.4 前向纠错和重传

有两种主要的纠错方法。向前纠错 forward error correction 是接收方通过使用冗余位尝试推测报文的方法。正如在后面看到的那样，如果差错的个数很小，这是可能的。

通过重传 retransmission 纠错，是接收方检测出有差错发生、并要求发送方重新发送报文的技术。重复重发，直到接收方认为到达的报文无差错（一般来说，不是所有的差错都可以被检测到)。

10.1.5 编码

通过各种编码方案实现冗余。发送方增加冗余位，通过某种方法建立「冗余位和真实数据位之间的某种关系」。接收方检测这两者的关系来检错或纠错。冗余位和数据位的比率、以及方法的健壮性是任何编码方案的重要因素。图10.3说明了编码的一般概念。

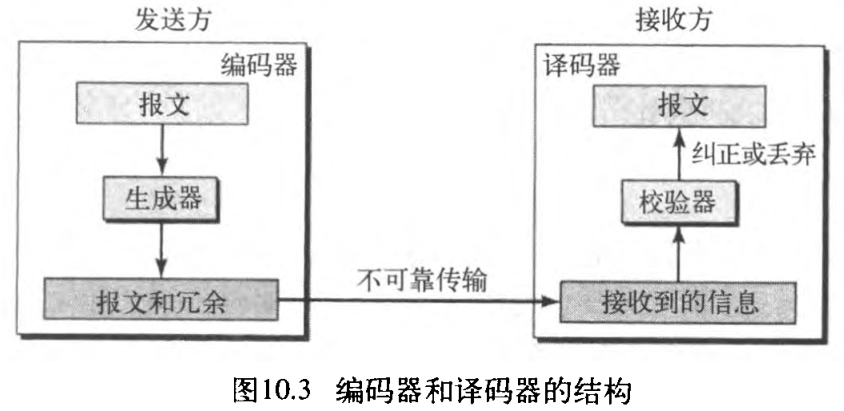
可以把编码方案分成两大类：块编码 block coding 和卷积编码 convolution coding 。这里只专注于块编码，而卷积编码更加复杂，超出了范围。

10.1.6 模运算

在模运算 modular arithmetic 中，只使用有限范围中的正整数。它的上限称为模数 modulus $N$ ，然后使用 $0$ 到 $N?1$ 的正整数。这是以 $N$ 为模数的运算。例如，如果模数是 $12$ ，我们只使用 $0$ 到 $11$ 的整数。时钟系统是模运算的一个实例。它基于以 $12$ 为模数的运算，$12$ 由 $0$ 代替。在模 $N$ 系统中，如果数字大于 $N$ ，则除以 $N$ 并取余数。如果它是负数，需要加上 $N$ 的倍数使其变为正整数。再次考虑时钟系统，如果在早上 $11$ 点开始工作，并且工作需要 $5$ 个小时，要么会说在 $16$ 点结束工作，或者会说在下午 $4$ 点结束（$16/12$ 的余数是 $4$ ）。

模运算中的加法和减法是简单的。在同一列上两个数字相加没有进位，在同一列上两个数字相减没有借位 There is no carry when you add two digits in a column. There is no carry when you subtract one digit from another in a column 。（？）

1. 模2运算

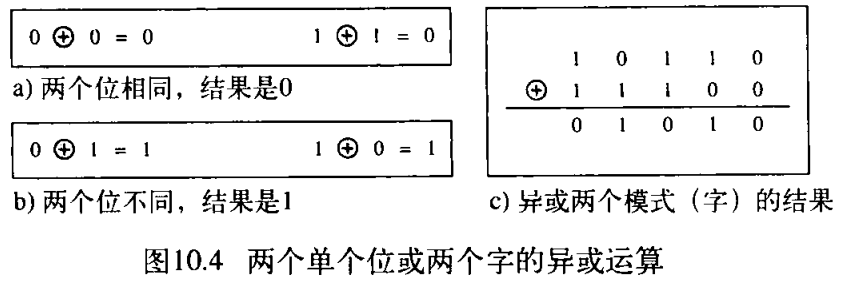
特别感兴趣的是模 $2$ 运算。在这个运算法中，模数 $N$ 为 $2$ 。我们只能使用 $0$ 和 $1$ 。这个运算的操作很简单。如下给出了如何加减 $2$ 个位。

• 加：$0+0=0,0+1=1,1+0=1,1+1=0$
• 减：$0?0=0,0?1=1,1?0=1,1?1=0$

特别注意，加法和减法给出了相同的结果。在这个运算中，对加法和减法，使用 XOR（异或）运算。如果两个位相同，XOR 运算的结果是 0；如果不同，则结果是 $1$ 。图10.4给出了这个运算。

2. 其他模数运算

其原理是相同的，使用 $0$ 到 $N?1$ 之间的正整数。如果模数不是 $2$ ，加法和减法是不同的。如果得到一个为负的结果，就加上倍数 $N$ 使其变成正整数。

10.2 块编码

在块编码中，我们把报文划分成块，每个块有 $k$ 位，称为数据字 dataword ，并增加 $r$ 个冗余位使其长度变为 $n=k+r$ ， 形成 $n$ 位的块称为码字 codeword 。如何选择或计算这额外的 $r$ 位将在后面讨论。目前重要的是知道，有一组长度为 $k$ 的数据字和一组长度为 $n$ 的码字。$k$ 位就有 $2^k$ 个数据字组合，$n$ 位就有 $2^n$ 个码字组合。既然 $n>k$，可能的码字数大于可能的数据字数。

块编码处理是一对一，相同的数据字总是编码成相同的码字。这意味着 $2^n?2^k$ 个码字没有使用，称这些码字为无效或非法码。图10.5说明了
这个情况。

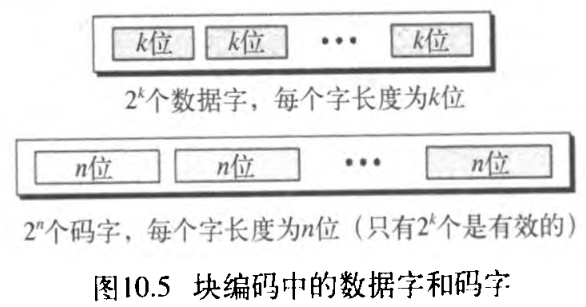
【例10.1】第4章中讨论过的 4B/5B 块编码是这种编码的一个好示例。在这个编码方案中，$k=4,n=5$ 。正如所看的那样，有 $2^k=16$ 个数据字以及 $2^n=32$ 个码字。$32$ 个码字中只有 $16$ 个用于报文传输，其余的 $16$ 个或者用于其他目的或者不用。

10.2.1 差错检测

如何使用块编码检测差错呢？如果满足以下两个条件，接收方就能检测出原来码字的一个差错 a change 。

1. 接收方有（或能够找到）有效码字的列表。
2. 原来码字已改变成无效的码字。

图10.6表示了差错检测中块编码的作用。

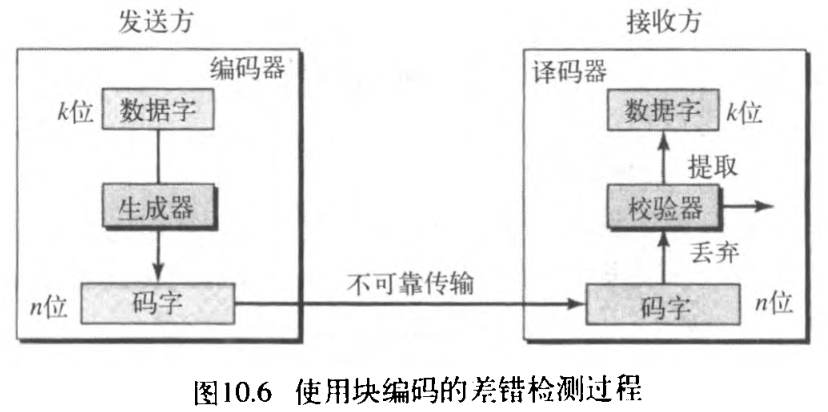
通过使用编码规则和过程的生成器（后面讨论），发送方根据数据字生成码字。每个发送给接收方的码字在传输中可能会出错。如果接收到的码字是有效码字中的一个，就接收这个码字，提取出对应的数据字；如果接收到的码字不是有效的，就将它丢弃。但是，如果码字在传输中被破坏，但接收到的码字仍然是一个有效的码字，差错就无法被检测到。这种类型的编码只能检测出简单的差错，两个或更多的差错可能就无法被检测到 This type ofcoding can detect only single errors. Two or more errors may remain undetected 。

【例10.2】假设 $k=2$ ，$n=3$ 。表10.1给出了数据字和码字列表。后面将会看到如何从数据字生成码字。假设发送方把数据字 $01$ 编码成 $011$ 并发送给接收方，考虑以下的情况：

1. 接收方接收到 $011$ ，它是有效的码字。接收方从它提取出数据字 $01$ 。
2. 码字在传输中被破坏，接收方接收到 $111$（最左边的位被破坏）。这是无效的码字被丢弃。
3. 码字在传输中被破坏，接收方接收到 $000$（右边两位被破坏）。这是个有效码字，接收方错误地提取出数据字 $00$ 。这两个破坏位形成的差错无法被检测到。
   

注意：差错检测码是根据某些类型的差错而设计的，因此只能检测到这些类型的差错，其他类型的差错无法被检测到。

10.2.2 纠错

如前述，纠错比检错更复杂。在检错中，接收方只需要知道接收到的码字是无效的。而在纠错中，接收方需要知道（或推测）发送的原来码字。可以说纠错比检错需要更多的冗余位。这个概念与检错一样，只是校验功能更加复杂。图10.7表示了纠错中块编码的任务。

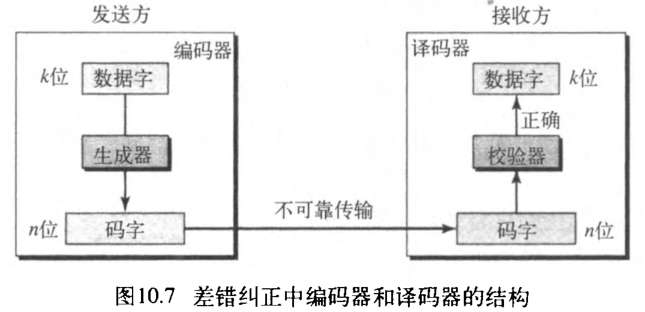
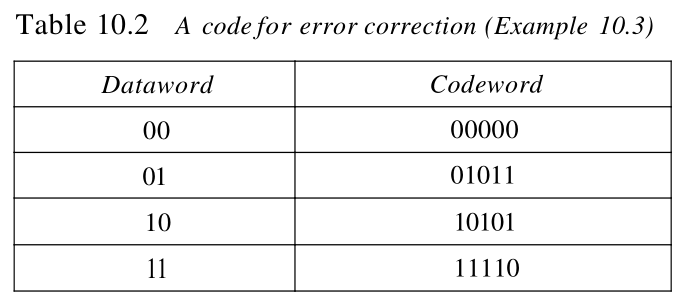
【例10.3】给例10.2加入更多的冗余位，看接收方在不知道实际发送的码字的情况下，是否能纠正差错。我们给 $2$ 位数据字加入 $3$ 个冗余位，形成 $5$ 位码字。后面会说明如何选择冗余位。现在集中说明纠错思想。表10.2给出了数据字和码字。
假设数据字是 $01$ 。发送方参照该表（或使用算法）生成码字 $01011$ 。这个码字在传输中被破坏，接收方接收到 $01001$（右边第 $2$ 位发生差错）。首先，接收方发现接收到的码字不在表中，这意味着发生了差错（必须在纠错前进行检错）。假定只有 $1$ 位被破坏，接收方使用以下策略来推测正确的码字。

1. 用表中第一个码字与接收到的码字进行比较 $01001$ 和 $00000$ ，因为有两位不同，所以接收方确定第一个码字不是发送的那个码字。
2. 相同的原因可知表中的第三个和第四个码字不可能是原来的码字。
3. 原来码字一定是表中的第二个码字，因为与接收到的码字只有一位不同。接收方用 $01011$ 代替 $01001$ ，并参照表找到原来数据字 $01$ 。
   

10.2.3 汉明距离

用于差错控制编码的一个核心概念是汉明距离。两个（相同长度）字的汉明距离Hamming distance 是对应位不同的数量。我们以 $d(x,y)$ 表示两个字 $x$ 和 $y$ 之间的汉明距离。

如果我们对两个字进行异或操作并计算 $1$ 的个数，就可以很容易地得出汉明距离。注意：汉明距离大于零。

【例10.4】让我们来导出下列两对字的汉明距离。

1. 汉明距离 $d$ $(000,011)$ 是 $2$ ，因为 $000\oplus 011$ 是 $011$（两个 $1$ ）。
2. 汉明距离 $d$ $(10101,11110)$ 是 $3$ ，因为 $10101\oplus 11110$ 是 $01011$（三个 $1$ ）。

10.2.4 最小汉明距离

虽然汉明距离概念是处理检错和纠错的核心概念，但是用于设计编码的度量是最小汉明距离。在→组字中，最小汉明距离 minimum Hamming distance 是一组字中所有可能对的最小汉明距离。我们以 $d_{\min }$ 定义编码方案中的最小汉明距离。为了得出这个值，我们导出所有字的汉明距离并选择最小值。

【例10.5】求表10.1中编码方案的最小汉明距离。
解：我们先求出所有的汉明距离。
$$\begin{array}{rl}d(000,011)=2& d(000,101)=2d(000,110)=2\\ d(011,101)=2& d(011,110)=2d(101,110)=2\end{array}$$ 得出 $d_{\min }=2$ 。

【例10.6】求表10.2中编码方案的最小汉明距离。
解：我们先求出所有的汉明距离。
$$\begin{array}{rl}d(00000,01011)=3& d(00000,10101)=3d(00000,11110)=4\\ d(01011,10101)=4& d(01011,11110)=3d(10101,11110)=3\end{array}$$ 得出 $d_{\min }=3$ 。

1. 三个参数

在继续讨论前我们需要注意到，任何编码方案需要至少三个参数：码字长度 $n$ ，数据字长度 $k$ ，以及最小汉明距离 $d_{\min }$ 。编码方案 $C$ 写成 $C(n,k)$ 和一个单独的 $d_{\min }$ 表达式。例如，可以把第一个编码方案写作 $C(3,2)$ 和 $d_{\min }=2$ ，把第二个写作 $C(5,2)$ 和 $d_{\min }=3$ 。

2. 汉明距离和差错

在探究检错和纠错的标准前，讨论汉明距离与传输中发生的差错之间的联系——当一个码字在传输中被破坏时，发送的码字和接收到的码字之间的汉明距离是差错影响的位数。换言之，接收到的码字和发送的码字之间的汉明距离是传输中破坏的位数。例如，如果发送的码字是 $00000$ 而接收到的码字是 $01101$ ，$3$ 个位发生差错，这两个码字间的汉明距离是 $d(00000,01101)=3$ 。

检错的最小距离

如果我们能够检测出最多 $s$ 个差错，那么让我们导出编码中的最小江明距离。如果 $s$ 个差错发生在传输中，发送的码字和接收到的码字间的汉明距离是 $s$ 。如果我们的编码能检测出最多 $s$ 个差错，那么两个有效编码间的最小汉明距离必须是 $s+1$ ， 这样接收到的码字才不会与有效码字匹配。换言之，如果所有有效码字间的最小距离是 $s+1$ ，那么接收到的码字才不会被错误地认为是另 一个正确的码字。对于距离小于 $(s+1)$ 的码字，接收方不会认为是有效码字，差错可以被检测到。

需要在这里澄清一点：虽然 $d_{\min }=s+1$ 的编码可能能够在某些特殊情况下检测出多于 $S$ 个差错，但是只有 $S$ 个或更少的差错可以保证被检测到。

【例10.7】我们第一个编码方案（表10.1）的最小汉明距离是 $2$ 。这个编码方案保证检测到单个差错 。例如，如果发送第三个码字 $101$ ，发生了一个差错，那么接收到的码字就不能与任何一个有效码字匹配。但是如果发生了两个差错，接收到的码字可能与某一个有效码字匹配，因此差错无法被检测到。

【例10.8】第二个编码方案（表10.2）有 $d_{\min }=3$ 。这个编码能检测到最多 2个差错。可以看到，当发送任一个有效码字肘，发生两个差错得到的码字不在有效码字表中，接收方不会被欺骗 。 但是，三个差错的一些组合会把一个有效码字改变成另一个有效码字。接收方会接收接收到的码字，而无法检测到差错 。

我们以几何意义看待这个问题。假设 发送的码字 $x$ 在以 $s$ 为半径的圆中心，所有其他接收到的发生 $1$ 到 $s$ 个差错的码字位于圆内或者圆周上，所有其余有效码字一定位于圆外，如图10.8所示 。

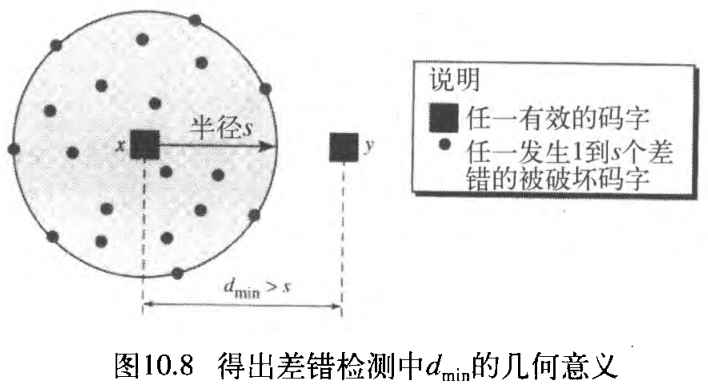
在图10.8中，$d_{\min }$ 一定是大于 $s$ 的整数，即 $d_{\min }=s+1$ 。

3. 纠错的最小距离

纠错比检错更复杂，它涉及一个决策。当接收到的码字不是有效的码字时，接收方需要确定实际发送的是哪一个码字。这个决策基于区域 territory 慨念，围绕码字的独占区域。每个有效码字都有自己的区域 Each valid codeword has its own territory 。

我们使用几何方法定义每个区域。假设每个有效码字有以 $t$ 为半径的圆形区域并且该有效码字在圆心。例如，假设码字 $x$ 被破坏的位小于或等于 $t$ 位，那么这个被破坏码字位于圆内或圆周上。如果接收方接收到属于该区域的一个码字，就确定原来的码字就是位于圆心的码字。注意：假设最多只能发生 $t$ 个差错，否则决策是错误的。图10.9说明了这个几何解释。有时也使用球体来说明所有有效块编码间的距离。

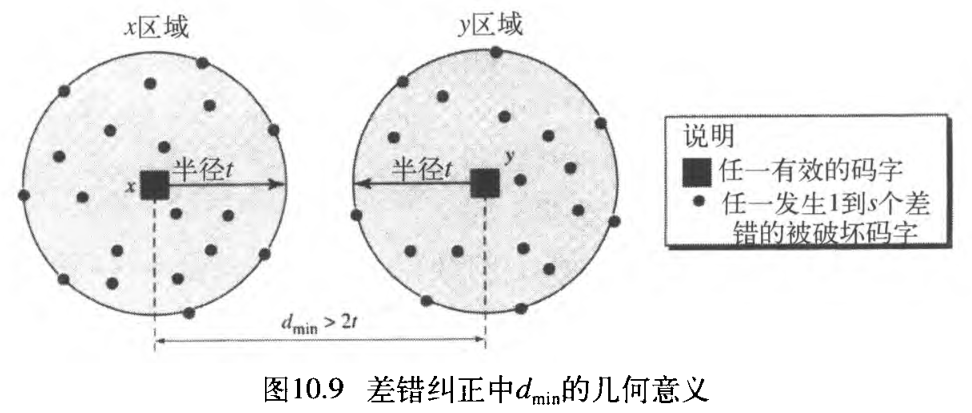
在图10.9中，$d_{\min }>2t$ ，因为下一个整数增量是 $1$ ，所以可以说 $d_{\min }=2t+1$ 。为了保证纠正所有情况下最多 $t$ 个差错，块编码中的最小汉明距离是 $d_{\min }=2t+1$。

【例10.9】一个编码方案有汉明距离 $d_{\min }=4$ 。这个方案的检错和纠错能力是多少？
解：这个方案保证检测到最多 $3$ 个差错 $s=3$ ， 但是它能纠正 $1$ 个差错。换言之，如果这个编码用于纠错，它的部分能力被浪费了。纠错编码需要的最小距离是奇数 $(3,5,7,\dots )$ 。

10.3 线性块编码

目前，几乎所有使用的块编码都属于一个称为线性块编码 Iinear block code 的子集。用于检错和纠错的非线性块编码的应用不是很广泛，因为它们的结构使得理论分析和实现都很困难。因此，只介绍线性块编码。

线性块编码的正式定义需要抽象代数（尤其是Galois领域）理论，这超出了范围。所以给出一个非正式定义。为此目的，线性块编码是一种由任何两个有效码字的异或（模2加法）产生另一个有效码字的编码（关于模 $2$ 封闭）。

【例10.10】观察定义在表10.1和表10.2中的两个编码是否属于线性块编码。

1. 表10.1中的方案是线性块编码，因为任何一个码字和任何另一个码字 XOR 的结果是一个有效码字。例如，第 $2$ 个和第 $3$ 个码字的 XOR 得到第 $4$ 个码字。
2. 表10.2中的方案也是线性块编码。我们可以通过异或两个其他码字得到所有的 $4$ 个码字。

10.3.1 线性块编码的最小距离

求出线性块编码的最小汉明距离很简单。最小汉明距离是「具有最少 $1$ 的个数的非零有效码字」中 $1$ 的个数。（？）

【例10.11】在第一个编码方案（表10.1）中，非零码字的 $1$ 的个数是 $2$ 、$2$ 和 $2$ 。因此，最小汉明距离是 $d_{\min }=2$ 。在第二个编码方案（表10.2）中，非零码字的 $1$ 个数是 $3$ 、$3$ 和 $4$ 。因此 $d_{\min }=3$ 。

10.3.2 一些线性块编码

现在展示一些线性块编码。这些代码很简单，因为我们可以很容易地找到编码和解码算法，并检验它们的性能。

1. 简单奇偶校验编码（检错）

可能最熟悉的差错检测编码是简单奇偶校验编码 simple parity-check code 。在这个编码中，$k$ 位数据字变成 $n$ 位码字，这里 $n=k+1$ 。选择称为奇偶位 parity bit 的额外位，使得码字中 $1$ 的总个数为偶数。虽然另一些实现规定 $1$ 的个数为奇数，但这里讨论偶数情况。

这种编码的最小汉明距离是 $d_{\min }=2$（Why？）， 这意味着编码是单个位检错编码，它不能纠正任何差错。

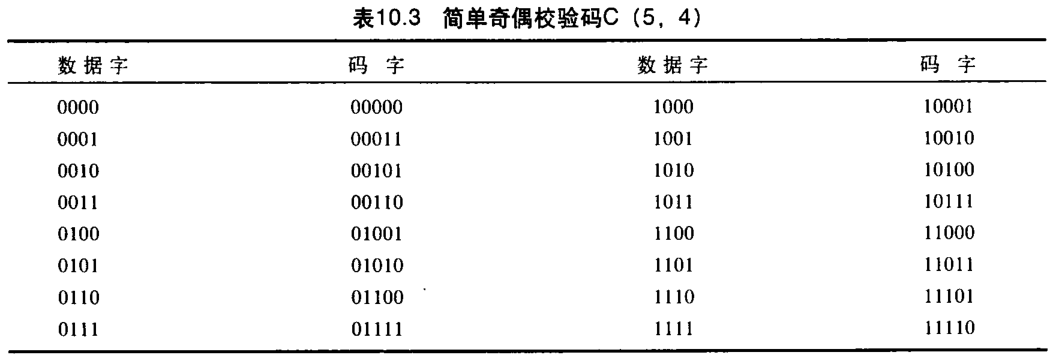
我们的第一个编码（表10.1）是 $k=2,n=3$ 的奇偶校验编码。表10.3中的编码也是奇偶校验编码，这里 $k=4,n=5$ 。

图10.10说明（在发送方）编码器和（在接收方）译码器的可能结构。编码器使用一个生成器，该生成器得到一个 $4$ 位数据字的副本 $(a_0,a_1,a_2,a_3)$ 并产生一个奇偶位 $r_0$ 。数据字的各个位和奇偶位组成一个 $5$ 位码字。增加的奇偶位使得码字中的 $1$ 的个数为偶数。


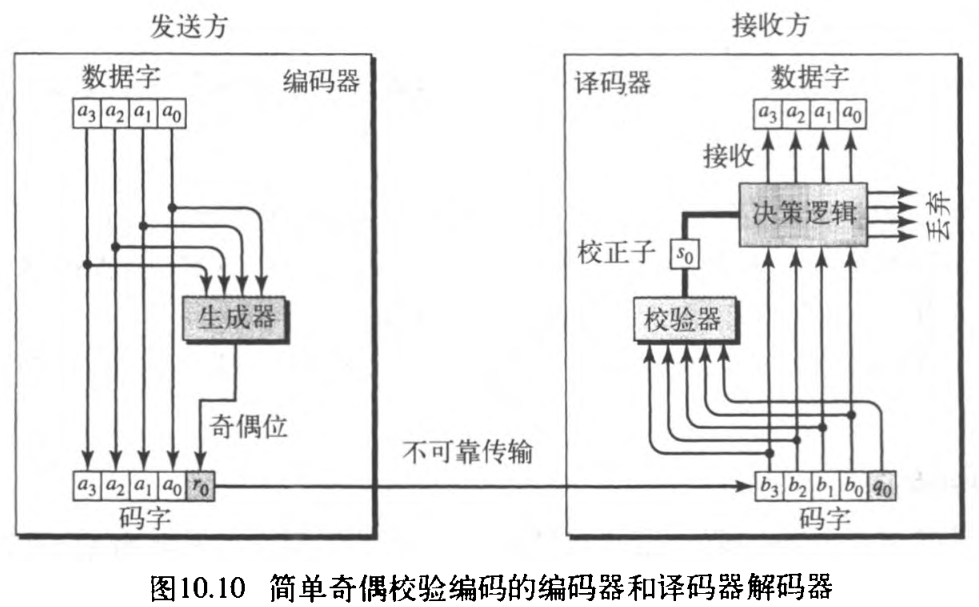
通常这是通过数据字的 $4$ 位做加法（模 $2$ 运算）实现，结果是奇偶位的值。换言之，$r_0=a_3+a_2+a_1+a_0$（模 $2$ 运算）。如果 $1$ 的个数是偶数，结果是 $0$ ，如果 $1$ 的个数是奇数，结果是 $1$ 。在这两种情况中，码字中 $1$ 的总个数是偶数。

发送方发送一个码字，该码字可能在传输中被破坏。接收方接收到一个 $5$ 位码字。接收方的校验器将做与发送方的生成器相同的工作，不同的是所有的 $5$ 位都要做加法，即 $S_0=b_3+b_2+b_1+b_1+q_0$（模 $2$ 运算）。计算结果 $S_0$ 称为校正子 syndrome ，只有 $1$ 位。当接收到的码字中 $1$ 的个数是偶数肘，校正子是 $0$ ，否则它是 $1$ 。

将校正子传递给决策逻辑分析器。如果校正子是 $0$ ，接收到的码字中没有差错，其中的数据部分作为数据字接收。如果校正子是 $1$ ，接收到的码字中的数据部分被丢弃。没有数据字生成。

【例10.12】看一些传输实况。假设发送方发送数据字 $1011$ 。从这个数据字生成的码字是 $10111$ 。它发送给接收方。我们检查五种情况：

1. 没有差错发生，接收到的码字是 $10111$ 。校正子是 $0$ ，生成数据字 $1011$ 。
2. 一个单个位差错改变了 $a_1$ ， 接收到的码字是 $10011$ 。校正子是 $1$ ，没有数据字生成。
3. 一个单个位差错改变了 $r_0$ ，接收到的码字是 $10110$ 。校正子是 $1$ ，没有数据字生成。注意：虽然没有数据字位被破坏，但是因为编码不够复杂，不能说明破坏位的位置，因此仍然没有数据字生成。
4. 一个差错改变了 $r_0$ ，第二个差错改变了 $a_3$ ，接收到的码字是 $00110$ 。校正子是 $0$ ，在接收方生成数据字 $0011$ 。注意：这里因为校正子为 $0$ ，会生成错误的数据字，简单奇偶校验译码器不能检测出偶数个差错，差错互相抵消使得校正子为 $0$ 。
   5.三个位 $a_3,a_2$ 和 $a_1$ 被差错改变，接收到的码字是 $01011$ 。校正子是 $1$ ，没有数据字生成。这说明==简单奇偶校验除了保证检测出一个单个位差错外，还能发现任何奇数个差错==。

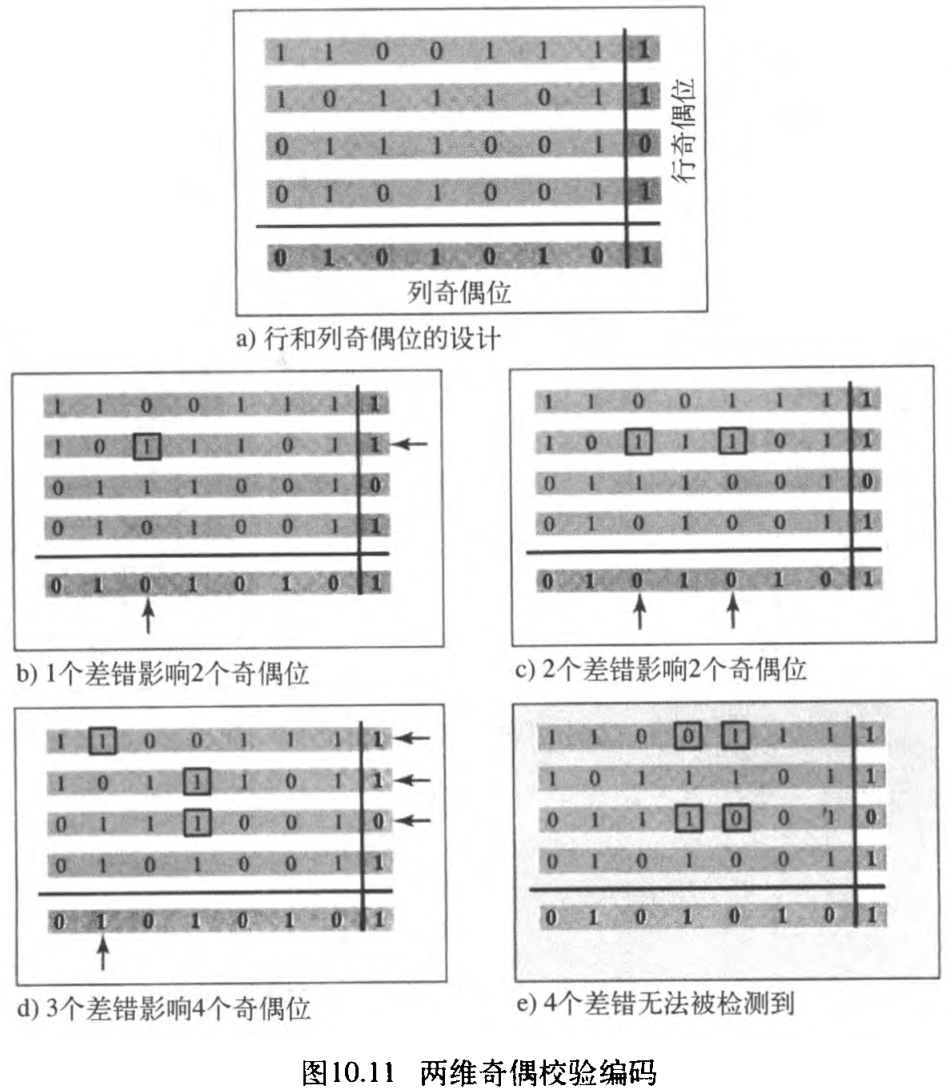
更好的办法是两维奇偶校验 two-dimensional parity check 。在这一方法中，数据字以表格形式（行和列）组织。在图10.11中，要发送的数据（ $5$ 个 $7$ 位字节）分别放在各自单独的行中。对于每一行和每一列，计算出一个奇偶校验位，然后将整个表发送给接收方，接收方将分别得出每一行和每一列的校正子。正如图10.11所示，两维奇偶校验能检测出表中任何位置发生的最多三个差错（箭头指向生成的非零校正子位置）。但是，影响 $4$ 位的差错可能无法检测到 errors affecting 4 bits may not be detected 。

2. 汉明编码

现在讨论称为汉明编码 Hamming code 的纠错编码。这些编码最初设计是 $d_{\min }=3$ ，这意味着它们能做最多检测出 $2$ 个差错和最多纠正 $1$ 个差错。虽然有一些汉明编码能纠正多于 $1$ 个差错，但这里的讨论只限于单个位纠错编码，即下面讨论的所有汉明编码都有 $d_{\min }=3$ 。

先找出汉明编码中 $n$ 和 $k$ 的关系。我们需要选择 $m\ge 3$ 的整数。然后从 $m$ 计算出 $n$ 和 $k$ ，分别为 $n=2^m?1$ 和 $k=n?m$ 。校验位个数 $r=m$ 。例如，如果 $m=3$ ，那么 $n=7,k=4$ 。 这就是 $d_{\min }=3$ 的汉明编码 $C(7,4)$ 。表10.4给出了这个编码的数据字和码字。
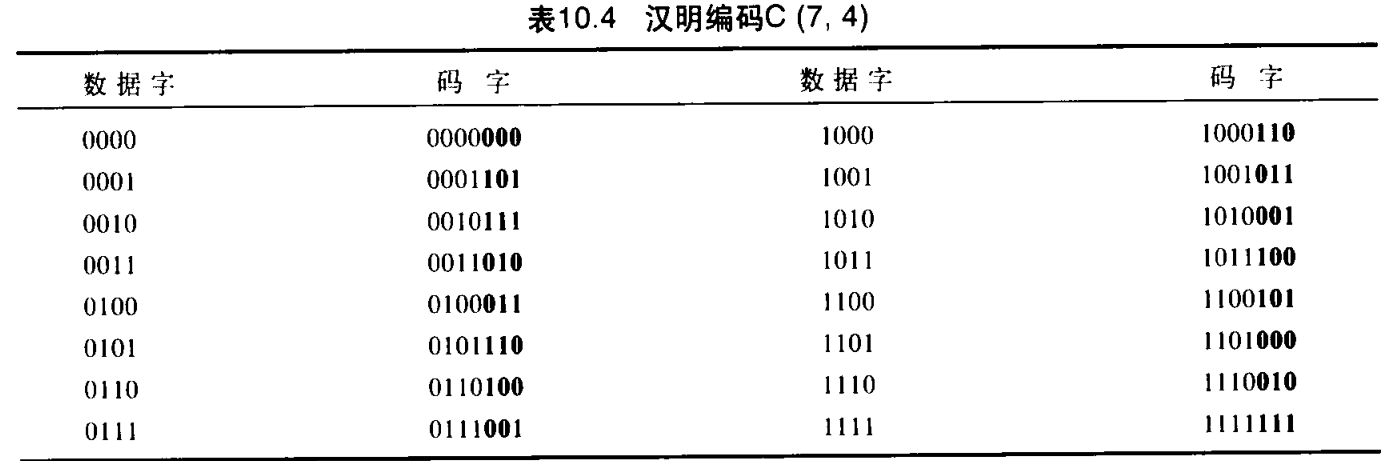图10.12给出了这个例子的编码器和译码器结构。

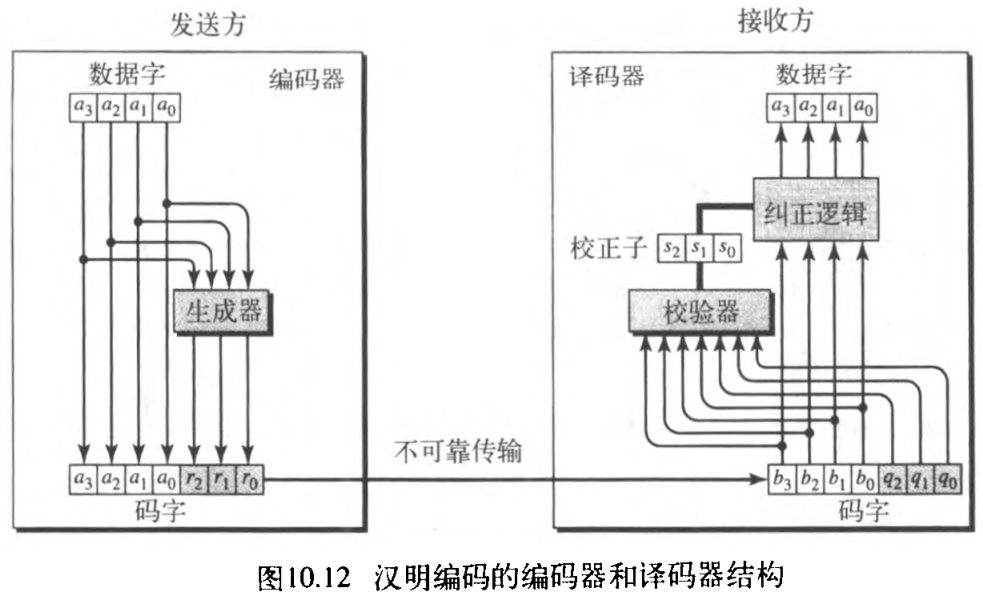
$4$ 位数据字的副本进入生成器，产生三个奇偶校验位 $r_0,r_1,r_2$ 。如下所示（用的仍是模 $2$ 运算）：
$$\begin{gathered} r_0=a_2+a_1+a_0 \\ {r}_1=a_3+a_2+a_1 \\ {r}_2=a_3+a_1+a_0 \end{gathered}$$ 换言之，每个奇偶校验位处理 $4$ 位数据字中的 $3$ 位。每个 $4$ 位组合（ $3$ 个数据字位和 $1$ 个奇偶位）中的 $1$ 的个数一定是偶数。我们并不是说这三个方程是唯一的，只要数据字 $4$ 位中取 $3$ 位生成独立等式（两个等式组合不能生成第三个等式）的任何三个等式是有效的。

校验器使用的等式与生成器使用的一样，奇偶校验位加到等式的右边。
$$\begin{gathered} s_0=b_2+b_1+b_0+q_0 \\ {s}_1=b_3+b_2+b_1+q_1 \\ {s}_2=b_3+b_1+b_0+q_2 \end{gathered}$$ $3$ 位校正子产生 $8$ 个不同的位模式（$000$ 到 $111$），这能表示 $8$ 种不同的情况。这些情况定义了接收到的码字中无差错或者 $7$ 位中有 $1$ 位有差错，如表10.5所示。
注意：生成器不关心表10.5的四种情况（无差错或奇偶位的差错）。在其他四种情况中，$4$ 位中相应的位必须反转（$0$ 变成 $1$ 或 $1$ 变成 $0$) 得出正确的码字。

表10.5中的几个校正子值，基于校正子位计算 syndrome bit calculations 。例如，如果 $q_0$ 发生差错 ，$s_0$ 是唯一受到影响的位，因此校正子是 $001$ 。如果 $b_2$ 发生差错 ，$s_0$ 和 $s_1$ 都受到影响，因此校正子是 $011$ 。类似地，如果 $b_1$ 发生差错，所有三个校正子位都受到影响，因此校正子是 $111$ 。

有两点需要在这里强调一下。第一点，如果在传输中发生两个差错，生成的数据字可能不是正确的数据字。第二点，如果想用上面的编码用于纠错，还需要独特的设计。

【例10.13】让我们跟踪 $3$ 个数据字从发送方到目的地的路径。

1. 数据字 $0100$ 变成码字 $0100011$ 。接收到码字 $0100011$ 。校正子是 $000$（无差错），最后的数据字是 $0100$ 。
2. 数据字 $0111$ 变成码字 $0111001$ 。接收到码字 $0011001$ 。校正子是 $011$ 。根据表10.5，$b_2$ 发生差错。反转 $b_2$ 后（$0$ 变成 $1$），最后的数据字是 $0111$ 。
3. 数据字 $1101$ 变成码字 $1101000$ 。接收到码字 $0001000$（两个差错）。校正子是 $101$ ，这意味着 $b_0$ 发生差错。反转 $b_0$ 后，我们得到 $0000$ ，这是错误的数据字。这说明我们的编码检测不到两个差错。

【例10.14】我们需要至少 $7$ 位的数据字。计算满足这个条件的 $k$ 值和 $n$ 值。
解：要求 $k=n?m$ 大于或等于 $7$ ，或者 $2^m?1?m\ge 7$ 。

1. 如果我们设 $m=3$ ， 结果是 $n=2^3?1=7,k=7?3=4$ ，这是不能接受的。
2. 如果我们设 $m=4$ ， 那么 $n=2^4?1=15,k=15?4=11$ ，这满足了条件。因此编码是 $C(15,11)$ 。有一些方法使得数据字为特定长度，但是这个问题的讨论和实现超出了范围。

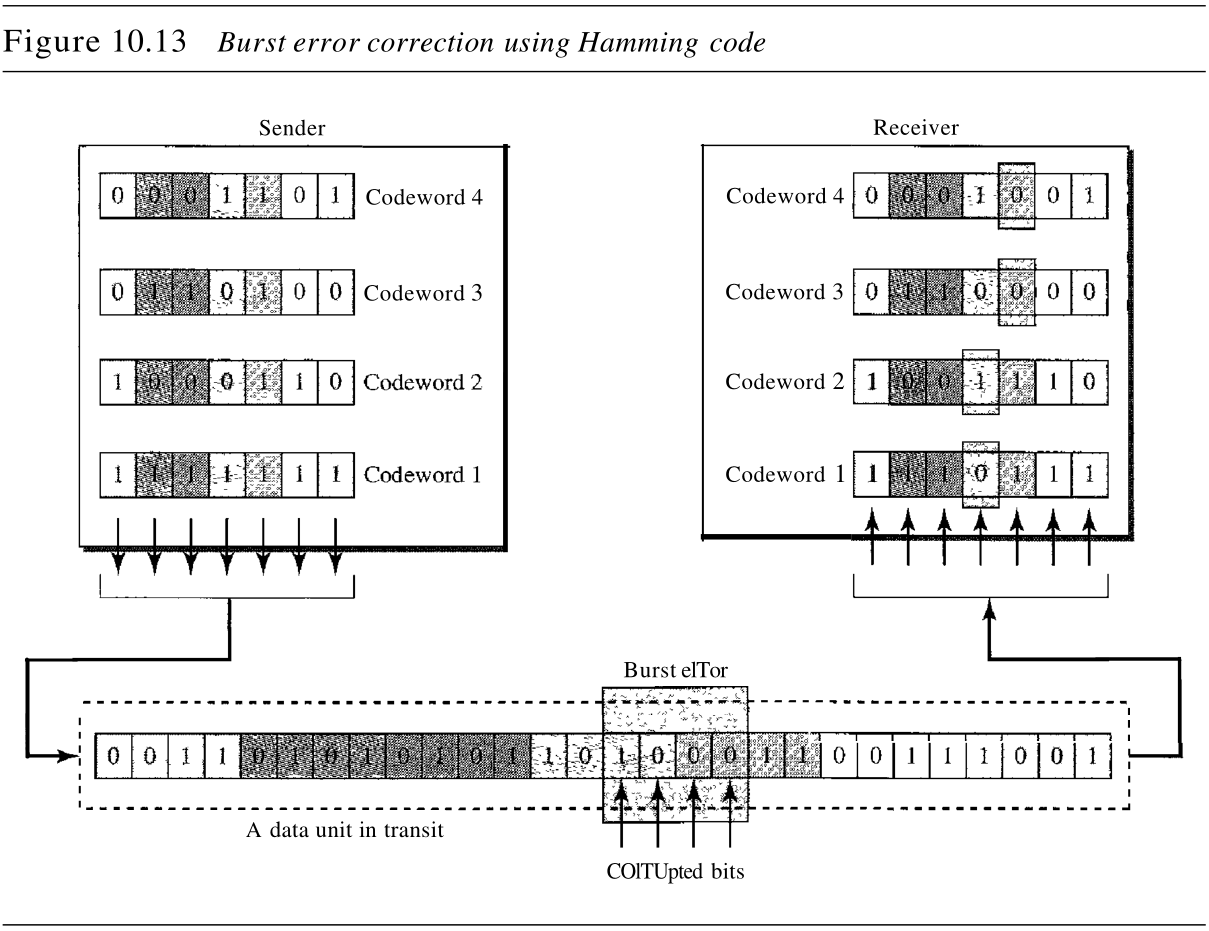
汉明编码只能纠正单个差错或检测出两个差错。但是，有方法使它能检测出突发差错，如图10.13所示。

关键思想是，在几个码字之间分割突发错误，每个码字只有一个错误。在数据通信中，我们通常发送数据分组或数据帧。为了让汉明编码能对长度为 $N$ 的突发差错起作用，需要从帧生成 $N$ 个码字。然后，不是每次发送一个码字，而是以表格形式组织码字，并每次发送表中一列的位。在图10.13中，以逐列发送位（从左边开始）。在每一列中，从底到顶发送位。在这种方式中，一个帧由 $4$个码字组成，并发送给接收方。图10.13说明长度为 $4$ 的突发差错破坏了这个帧，每个码字只有 $1$ 位被破坏。每个码字被破坏的位在接收方，可以轻易地被纠正（？）。

10.4 循环编码

循环编码是有一个附加性质的特殊线性块编码。在循环编码 cyclic code 中，如果码字循环移位（旋转），则其结果是另一个码字。例如，如果 $1011000$ 是一个码字，循环左移，那么 $0110001$ 也是一个码字。在这种情况中，如果称第一个码字中的位（从右至左）为 $a_0$ 到 $a_6$ ，那么称第二个码字中的位为 $b_0$ 到 $b_6$ ，我们可以通过如下方式进行移位：
$$b_1=a_0,b_2=a_1,b_3=a_2,b_4=a_3,b_5=a_4,b_6=a_5,b_0=a_6$$ 在最右的等式中，第一个码字中的最后一位变成了第二个码字中的第一位。

10.4.1 循环冗余校验

我们能够生成循环编码来纠错，但所需的理论背景超出了范围。在本节中，简单地讨论一种称为循环冗余校验 cyclic redundancy check, CRC 的循环编码，它用于诸如LAN和WAN的网络中。图10.14说明了编码器和译码器的一种可能设计，表10.6给出了CRC编码的一个例子，可以看到这个编码具有的线性特性和循环特性。


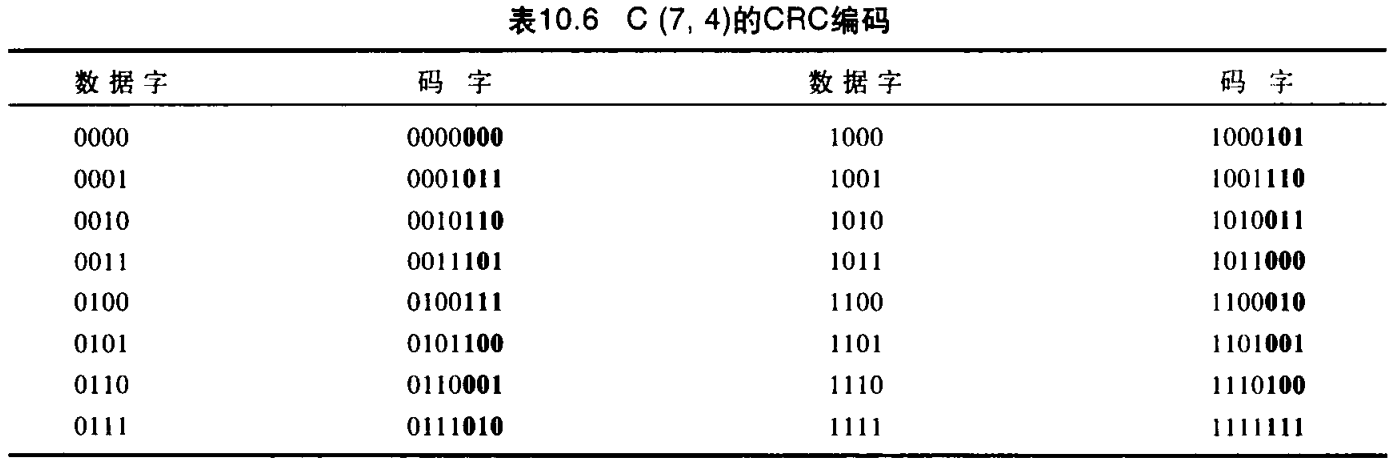
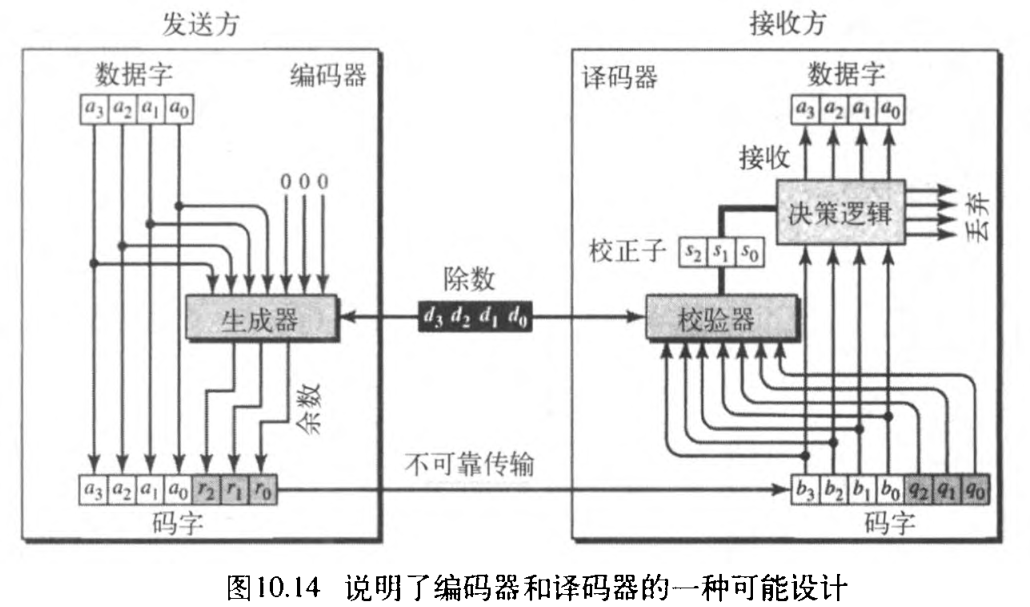
在编码器中，数据字有 $k$ 位（这里 $k$ 是 $4$），码字有 $n$ 位（这里 $n$ 是 $7$）。在数据字的右边加上 $n?k$（这里是 $3$）个 $0$ 位，长度加 $3$ 。$n$ 位结果传给生成器，生成器使用长度为 $n?k+1$（这里是 $4$）的除数，这个除数是预定义并经双方同意的。生成器用除数除增加后的数据字（模 $2$ 除法），除法的商被丢弃，余数 $r_2{r}_1{r}_0$ 加到数据字上生成码字。

译码器接收到可能被破坏的码字。全 $n$ 位的副本传递给校验器，它是生成器的复制品。校验器产生的余数是 $n?k$（这里是 $3$）位的校正子，它被传递给决策逻辑分析器。分析器是一个简单的函数。如果校正子全 $0$ ，码字最左边的 $4$ 位被接收为数据字（被认为无差错），否则，这 $4$ 位被丢弃（有差错）。

1. 编码器

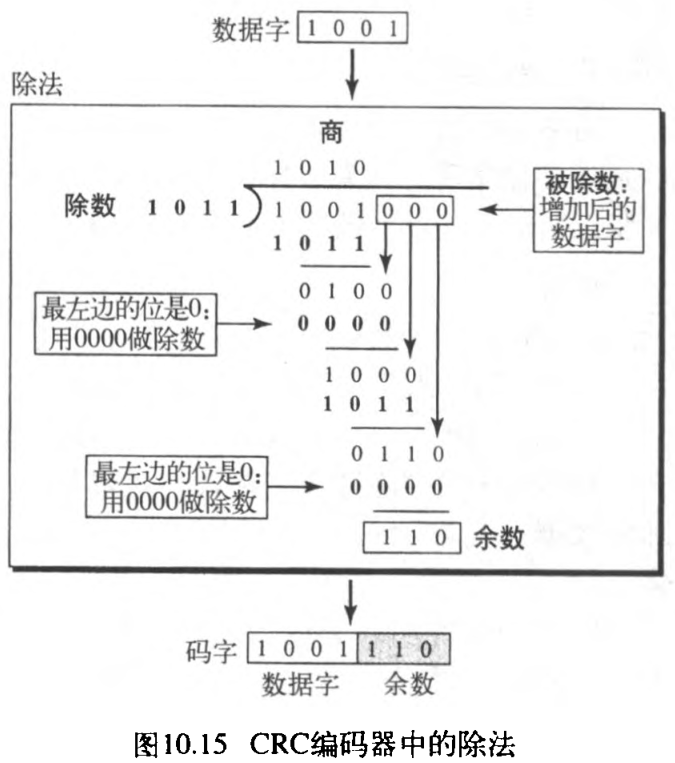
仔细考察编码器。编码器将得到的数据字加上 $n?k$ 个 $0$ ，然后它用除数除以扩充后的数据字。如图10.15所示。

模 $2$ 二进制除法过程与熟悉的用于十进制数字的除法过程是一样的。但是，正如在开始所提到的，此时加法和减法一样的，我们使用异或操作来做加法和减法。像在十进制除法中一样，处理过程逐步完成。在每一步，除数的副本与被除数的 $4$ 位进行异或操作。异或运算的结果（余数）是 $3$ 位（在这种情况中），$1$ 个额外位移下来、加上去组成 $4$ 位进行下一步。当没有可移下来的位时，就得到了结果。$3$ 位余数形成了校验位 $(r_2{r}_1{r}_0)$ 。它们附加在数据字上生成码字。

在这种除法中有重要的一点需要记住：如果被除数（用于每一步的部分）的最左边的位是0 ，这一步就不能使用正常的除数，需要使用全 $0$ 的除数。

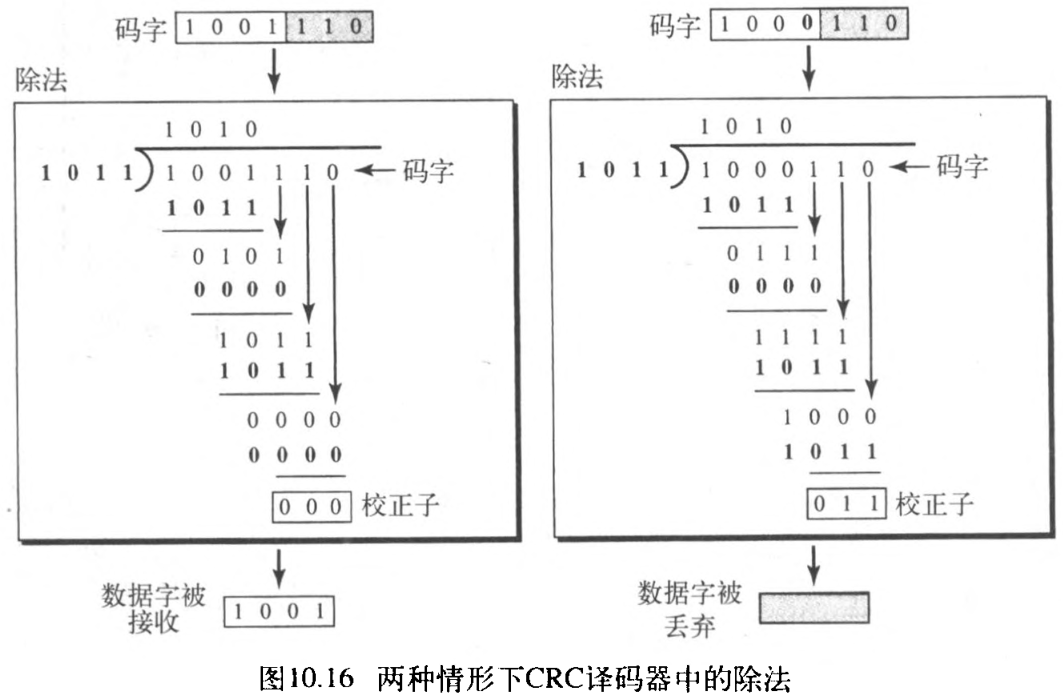
2. 译码器

码字可能会在传输中改变。译码器执行与编码器相同的除法处理。除法的余数是校正子。如果校正子是全 $0$ ，就没有差错，数据字从接收到的码字中分离出来并被接收。否则，整个码字被丢弃。图10.16说明了两种情形：左边的图说明当没有差错发生时的校正子，其为 $000$ 。右边的图说明有单个差错发生的情形，校正子不是全 $0$（它是 $011$）。

3. 除数

可能想知道如何选择除数 $1011$ 。在后面会给出一些标准，但是通常它涉及抽象代数。

10.4.2 硬件实现

循环编码的一个优点是，通过使用少量的电子设备，编码器和译码器就可以轻松且廉价地在硬件中实现。还有，硬件实现增加了校验位和校正子位计算的比率。在本节尝试逐步说明这个过程。

1. 除数

选择基于在异或操作中活动的增强数据位部分的最左边位。
先来考虑除数。需要注意如下几点：

1. 除数重复地与被除数部分进行异或运算；
2. 除数有 $n?k+1$ 位，或者是预定义的，或者全为 $0$ 。换言之，这些位不会随数据字改变。在前面的例子中，除数或者是 $1011$ 或者是 $0000$ 。具体选哪一个，取决于异或运算中起作用的增广数据字 augmented dataword（被除数）部分的最左边一位；
3. 进一步说明在异或运算中除数只需要 $n?k$ 位，不需要最左边的一位。因为无论这个位的值是什么运算，其结果永远是 $0$ 。原因是异或操作的输入或者都是 $0$ 或者都是 $1$ 。在前面的例子中，只有 $3$ 位（而不是 $4$ 位）实际用于异或运算中。

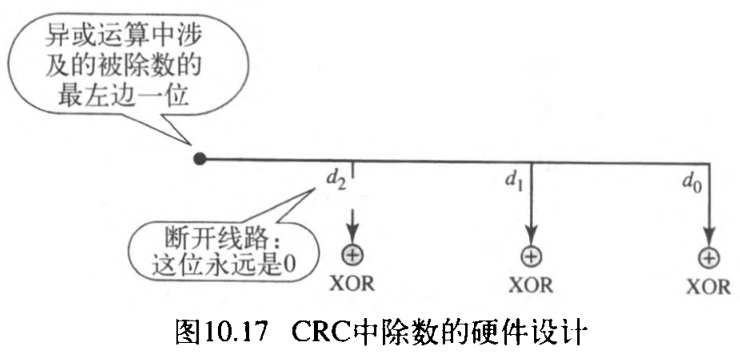
根据这几点，如果我们知道除数的模式，就能生成可用于循环编码的固定（硬件线路的）除数。图10.17给出了这样一个用于前面例子的设计，还显示了用于运算的异或设备。

注意：如果用于这一步的被除数部分的最左边一位是 $1$ ，除数位 $(d_2{d}_1{d}_0)$ 是 $011$ ，如果最左边一位是 $0$ ，则除数位是 $000$ 。这个设计根据最左边位做出正确的选择 。

2. 增广数据字

在图10.15中的纸笔除法过程中，我们将增广数据字显示为固定位置，而将除数向右位移，每一步移 $1$ 位，除数各位与增广数据字各位正好对齐。既然除数是固定的，那么我们需要把增广数据字向左位移（反方向），使得除数的各位正好对齐。不需要保存增广数据字的各位。

3. 余数

在前面的例子中，余数的长度是 $3$ 位（一般 $n?k$ 位)。可以使用 $3$ 个寄存器（单个位存储设备）来保存这些位。为了得到除法的最终余数，需要修改除法过程。下面是以硬件（或者甚至以软件）模拟除法的过程。

1. 假设余数初始为全 $0$（我们的例子中是 $000$ ）。
2. 在每个时间节拍（增广数据字每到来 $1$ 位) ，重复以下两个处理过程：
   • 我们使用最左边的位来决定除数（$011$ 或 $000$ ），从而得到余数。
   • 余数的其他 $2$ 位和增广数据字的下一位（一共 $3$ 位），与 $3$ 位除数进行异或运算得出下一个余数。

图10.18表示了这个模拟过程。但是注意，这不是最终设计，最终设计将会有更大的改进。每个时间节拍用不同的时间表示，增广数据字的一位用于异或运算。如果仔细观察这个设计有 $7$ 个步骤，而用纸笔运算时只有 $4$ 个步骤。增加了前 $3$ 个步骤，是为了使得每个步骤一样、以及每个步骤的设计一样。步骤 $1$ 、$2$ 和 $3$ ，把前 $3$ 位压进余数寄存器，步骤 $4$ 、$5$ 、$6$ 和 $7$ 与纸笔运算相匹配。注意，步骤 $4$ 到 $7$ 的余数寄存器中的值，正好与纸笔运算中的值相匹配。最后的余数也一样。

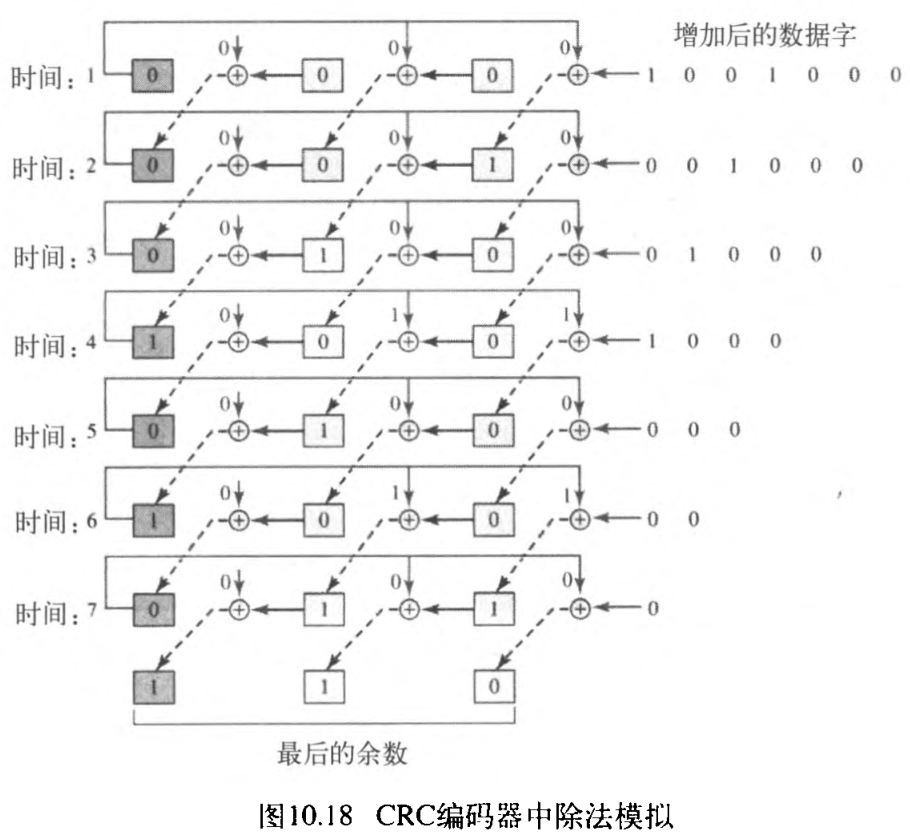
上面的设计只是为了展示，它需要简化才能用于实际。

• 首先，不需要保持余数各位的中间值，只需要最后的值。因此，只需要 $3$ 个寄存器而不是 $24$ 个。
• 在异或运算后，不需要前一个余数的各位值。还有，不需要 $21$ 个异或设备，两个就足够了，因为如果一个位是 $0$ ，异或运算的输出就是另一个位的值，另一个位就可以用于输出。

使用这两个修改，设计变得极其简单也更便宜，如图10.19所示。
但是，需要把寄存器改成移位寄存器。在一个时钟节拍期间，$1$ 位移位寄存器保存 $1$ 位。在每个时间节拍点，移位寄存器从输入端口接收一个位，存储新的位，并显示在输出端口。其内容和输出保持一致，直到下一个输入到来。当把若干个 $1$ 位移位寄存器连接在一起，它看起来好像寄存器的内容在移位。

4. 一般设计

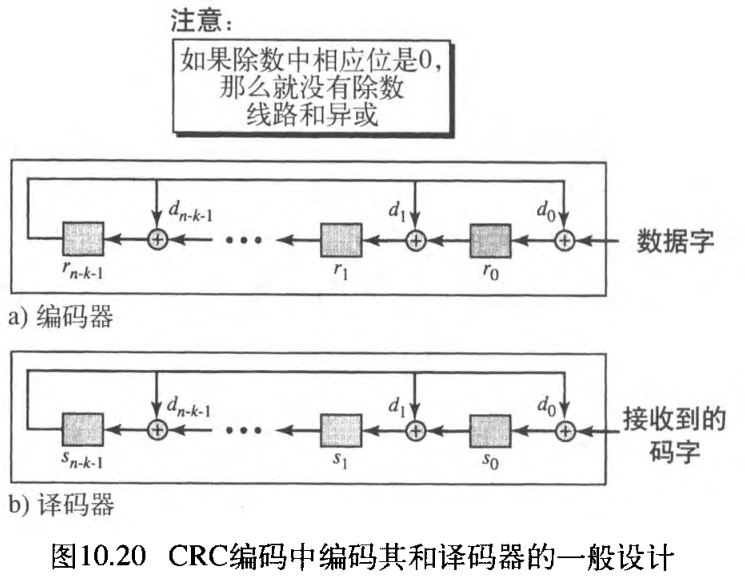
一个编码器和译码器的一般设计如图10.20所示。注意：在编码器和译码器中有 $n?k$ 个 $1$ 位移位寄存器。最多有 $n?k$ 个异或设备，但是除数通常在它们的模式中有若干个 $0$ ，这可以减少设备的数量。

还要注意：是数据字作为输入，而不是增广数据字，因为数据字中的位输入到编码器后，附加的位（全为 $0$ ) 不会影响最右边的异或。当然，在生成校验位前，这个处理还需要继续另外 $n?k$ 个步骤。 这个事实是对这个设计的批评之一。更好的方案设计能消除这个等待时间（校验位在 $k$ 步后就生成），可把这个留作研究课题。然而，在译码器中，整个码字在校正子生成前，必须输入到译码器。

10.4.3 多项式

理解循环编码以及如何分析它们的更好办法是，将它们表示为多项式。若干个 $0$ 和 $1$ 组成的模式，可以表示为以 $0$ 和 $1$ 为系数的多项式 polynornial 。每一项的幂次表示位所在的位置，系数表示位的值。

图10.21给出了一个二进制模式和它的多项式表示。在图10.21a中，说明了如何把二进制模式翻译成多项式。在图10.21b中说明了如何通过除去系数为 $0$ 的项并用 $x$ 代替 $x^1$ 、$1$ 代替 $x^0$ 来简化多项式。

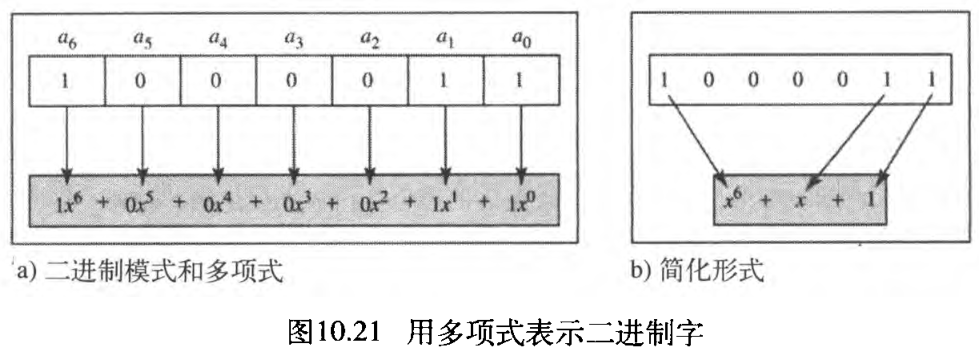
图10.21说明了一个显而易见的好处，$7$ 位模式可以用 $3$ 项表示 。当遇到诸如 $x^{23}+x^3+1$ 的多项式时，好处更加突出。这里模式是 $24$ 位长（$3$ 个 $1$ 和 $21$ 个 $0$) ，而用多项式表示时只有 $3$ 项。

1. 多项式的次数

多项式的次数是多项式中的最高幂次。例如，多项式 $x^6+x^3+1$ 的次数是 $6$ 。注意多项式的次数比二进制模式中位数少 $1$ 。这种情况下位模式有 $7$ 位。

2. 多项式加减法

数学上的多项式加减是通过加减相同幂次项的系数。此时系数只有 $0$ 和 $1$ ，加是模 $2$ 加法。两个结论。第一，加和减相同。第二，加减是删除相同项，把不同项合在一起。例如 $x^5+x^4+x^2$ 和 $x^6+x^4+x^2$ 的结果是 $x^6+x^5$ 。$x^4$ 和 $x^2$ 被删除。然而，注意：如果 $3$ 个多项式相加，有 $3$ 个项 $x^2$ ， 就删除其中 $2$ 个保留 $1$ 个。

3. 项乘法和除法

在这个算术中，一个项乘以另一个项很简单，只是幂次相加。例如 $x^3\times x^4$ 是 $x^7$ 。对于除法，只需第一个幂次减去第二个幂次即可。例如 $x^5÷x^2$ 是 $x^3$ 。

4. 两个多项式相乘

一个多项式乘以另一个多项式通过项乘项完成。第一个多项式的每一个项必须乘以第二个多项式的所有项。然后相同项对被删除化，简其结果。一个实例如下：
$$\begin{gathered} (x^5+x^3+x^2+x(x^2+x+1) \\ =x^7+x^6+x^5+x^5+x^4+x^3+x^4+x^3+x^2+x^3+x^2+x=x^7+x^6+x^3+x \end{gathered}$$

5. 一个多项式除另一个多项式

从概念上来说，多项式除法与编码器中讨论的二进制除法相同。被除数位的第一项除以除数的第一项。得到商的第一项。然后，将这一项乘以除数的结果从被除数中减去，重复这个过程直到被除数次数小于除数为止。稍后给出一个除法例子。

6. 移位

二进制模式时常左移或右移若干位。左移表示在右边加上若干个额外 $0$ ，右移表示删除右边若干位。左移通过每一项乘以 $x^m$ 实现，这里 $m$ 是移动的位数；右移通过每一项除以 $x^m$ 实现。下面说明了左移和右移。注意，在多项式中没有负幂次。

• 左移 $3$ 位：$10011$ 变成 $10011000$ ，$x^4+x+1$ 变成 $x^7+x^4+x^3$
• 右移 $3$ 位：$10011$ 变成 $10$ ，$x^4+x+1$ 变成 $x$

在图10.15编码器中的增广数据字实际上是左移了若干位。还要注意，连接两个位模式就是左移第一个多项式、再加上第二个多项式 we concatenate two bit patterns, we shift the first polynomial to the left and then add the second polynomial 。

7. 使用多项式的循环编码编码器

已经讨论过了多项式运算，现在说明如何从数据字生成码字。图10.22是图10.15的多项式的表示形式。可以看到这个过程更短。数据字 $1001$ 表示为 $x^3+1$ 。除数 $1011$ 表示为 $x^3+x+1$ 。为了得到增广数据字，先把数据字左移 $3$ 位（乘以 $x^3$）。其结果是 $x^6+x^3$ 。

除法是直接的，用被除数的第一项 $x^6$ 先除以除数的第一项 $x^3$ 。商的第一项是 $x^6÷x^3=x^3$ 。然后，被除数减去 $x^3$ 乘以除数（根据前面的减法定义）得到结果，结果的第一项是 $x^4$ ，它的次数大于除数的次数。继续除，直到余数的次数小于除数的次数。

可以看到在这个例子中，多项式表示简化了除法运算，因为这里不再需要涉及全 $0$ 除数的两个步骤（当然，人们可以将二进制除法中全 $0$ 除数的步骤也去掉）。在多项式表示中，循环编码中的除数通常称为生成多项式 $t(x)$ 或简称为生成器。

10.4.4 循环编码分析

我们可以使用多项式来分析循环编码的能力。定义了如下多项式，这里 $f(x)$ 是二进制系数的多项式。

• 数据字：$d(x)$ ，码字：$c(x)$ ，生成多项式：$g(x)$
• 校正子：$s(x)$ ，差错：$e(x)$

如果 $s(x)$ 不为 $0$ ，那么一位或多位被破坏。但是，如果 $s(x)$ 为 $0$ ，或者没有位被破坏、或者「有一些位被破坏，但译码器无法检测到任何差错」。在循环编码中，

在我们的分析中，必须施加在生成器g（x）上的标准，以检测我们特别想要检测的错误类型。

在分析中，我们希望找到生成多项式 $g(x)$ 上的标准，使得我们能检测出那些想检测出的差错类型。先找到发送的码字、差错、接收到的码字和生成多项式之间的关系。可以说
$$接收到的码字=c(x)+e(x)$$ 换言之，接收到的码字是发送的码字和差错之和。接收方用 $g(x)$ 除接收到的码字，得到校正子。可以写成
$$\frac{接收到的码字}{g(x)}=s(x)=\frac{c(x)+e(x)}{g(x)}=\frac{c(x)}{g(x)}+\frac{e(x)}{g(x)}$$

等式右边的第一项没有余数（根据码字的定义），因此，校正子实际上是右边第二项的余数。

如果这一项没有余数（校正子 $=0$），即 $e(x)$ 为 $0$ 或者 $e(x)$ 可以被 $g(x)$ 整除。不必担心第一种情况（没有差错），第二种情况很重要。在循环编码中，那些可以被 $g(x)$ 整除的差错无法被捕捉到。

先说明一些特殊的差错，看看它们如何被设计好的 $g(x)$ 捕捉到。

1. 单个位差错

$g(x)$ 的组成应该怎样，才能保证检测到单个位差错？单个位差错是 $e(x)=x^i$ ，这里 $i$ 是差错位的位置。如果单个位差错被捕捉到，那么 $x^i$ 不能被 $g(x)$ 整除（注意：当我们说不能整除时，表示它有余数）。如果 $g(x)$ 至少有两项（通常是这样的）并且 $x^0$ 的系数不为 $0$（最右边的位为 $1$ ），那么 $e(x)$ 不能被 $g(x)$ 整除，所有单个位差错都可以被捕捉到。

【例10.15】如下哪个 $g(x)$ 可以保证捕捉到单个位差错？对于每种情况，不能捕捉的差错是什么？
a. $x+1$
b. $x^3$
c. $1$
解：

• a. 没有一个 $x^i$ 可以被 $x+1$ 整除。换言之 ，$x^i/(x+1)$ 总有余数。因此，校正子不是零。任何单个位差错都可以被捕捉到。
• b. 如果 $i$ 大于或等于 $3$ ，$x^i$ 可以被 $g(x)$ 整除，$x^3$ 的余数是 $0$ ，接收方会被蒙蔽而认为没有差错，虽然实际是一个差错。注意：这种情况下，被破坏的位必须位于第 $4$ 位或更高位。能捕捉到位 $1$ 到位 $3$ 的单个差错。
• c. $i$ 的所有值使得 $x^i$ 可以被 $g(x)$ 整除。没有单个位差错可以被捕捉到。另外 ，$g(x)$ 是无用的，因为它表示的只是增加了 $n?k$ 个 $0$ 后的数据字的码字。

2. 两个独立的单个位差错

现在想像有两个独立的单个位差错。什么情况下这种类型的差错可以被捕捉到？可以把这种差错表示为 $x^j+x^i$ 。$i$ 和 $j$ 的值只表示差错的位置，差 $j一i$ 表示两个差错的距离，如图10.23所示。

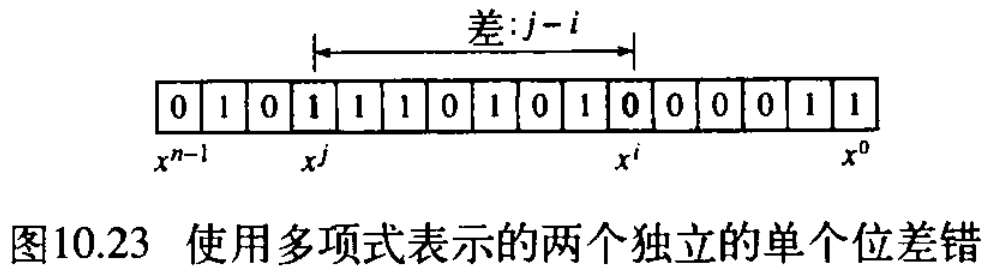
可以写成 $e(x)=x^i(x^{j?i}+1)$ 。如果 $g(x)$ 多于一项并且其中一项为 $x^0$，那么正如在前面看到的，它不能整除 $x^i$ 。因此，如果 $g(x)$ 能整除 $e(x)$ ， 那么它一定能整除 $x^{j?i}+1$ 。换言之，要使得 $g(x)$ 不能整除 $e(x)$ ，$g(x)$ 就一定不能整除 $x^t+1(0\le t\le n?1)$ ，这里 $t$ 在 $0$ 和 $n?1$ 之间，但是 $t=0$ 是无意义的，并且稍后会看到需要 $t=1$ 。这就表示 $t$ 应该在 $2$ 和 $n?1$ 之间。

总之，如果生成多项式不能整除 $x^t+1$（$t$ 在 $2$ 和 $n?1$ 之间) ，那么所有独立的双差错都能被检测到。

【例10.16】求出以下与两个独立的单个位差错相关的生成多项式的情况。
a. $x+1$
b. $x^4+1$
c. $x^7+x^6+1$
d. $x^{15}+x^{14}+1$
解：

• a. 对生成多项式来说，这是一个很差的选择，任何两个相邻的差错都不能被检测到。如 $e(x)=x^{i+1}+x^i=x^i(x+1)(i\ge 0)$ ，显而易见，$e(x)$ 能整除 $g(x)=x+1$ 。
• b. 这个生成多项式不能检测到相隔 $4$ 个位置的两个差错。这两个差错能位于任何位置，但是如果它们的距离是 $4$ ，仍然无法被检测到。
• c. 这是个好的选择。
• d. 如果 $t$ 小于 $32768$ ，这个多项式不能整除类型为 $x^t+1$ 的任何差错。这表示，一个码字中两个独立的差错相邻或者最多离开 $32768$ 位，都能被这个生成多项式检测到。

3. 奇数个差错

包含因子 $x+1$ 的生成多项式可以捕捉所有奇数个差错，这表示需要把 $x+1$ 作为任何生成多项式的因子。注意：不是说生成多项式本身应该是 $x+1$ ， 而是说它应该有因子 $x+1$ 。 如果它只是 $x+1$ ，那么它不能捕捉到两个相邻的独立差错（见前一节）。例如对 $x^4+x^2+1$ 能捕捉到所有奇数个差错，因为它可写作两个多项式 $x+1$ 和 $x^3+x^2+1$ 的乘积。

4. 突发性差错

现在把分析扩展到突发性差错，它是所有差错中最重要的。一个突发性差错的形式是 $e(x)=(x^j+?+x^i)$ 。注意：突发性差错和两个独立的单个位差错的不同，第一种有两项或更多项、而第二种只有两项。我们可以分解出因子 $x^i$ ，把差错 $e(x)$ 写成 $x^i(x^{j?i}+\dots +1)$ 。

如果生成多项式能检测到单个差错（对于生成多项式的最小条件），那么它不能整除 $x^i$ 。我们应该关注的是能整除 $x^{j?i}+\dots +1$ 的那些生成多项式。反过来说，$(x^{j?i}+\dots +1)/(x^r+\dots +1)$ 的余数一定不是 $0$ ，这样才能检测出差错。注意分母是生成多项式。可能有三种情况：

1. 如果 $j?i<r$ ，余数永远不会是 $0$ 。我们可以写成 $j?i=L?1$ ，这里 $L$ 是差错的长度。因此 $L?1<r$ 、$L<r+1$ 或 $L\le r$ 。这表示，所有长度小于或等于校验位数目 the number of check bits $r$ 的突发性差错，都会被检测到。
2. 在一些少见的情况中，如果 $j?i=r$ 或 $L=r+1$ ， 校正子是 $0$ ，差错无法被检测到。这可以在这些情况中得到验证，长度是 $r+1$ 的突发性差错，无法被检测到的概率是 $(1/2{)}^{r?1}$ 。例如，如果我们的生成多项式是 $x^{14}+x^3+1$ ， 这里 $r=14$ ，那么长度 $L=15$ 的突发性差错概率是 $(1/2{)}^{14?1}$ ，即几乎 $10000$ 中有 $1$ 个无法被检测到。
3. 在一些少见的情况中，如果 $j?i>r$ 或 $L>r+1$ ， 校正子是 $0$ ，差错无法被检测到。这可以在这些情况中得到验证，长度大于 $r+1$ 的突发性差错，无法被检测到的概率是 $(1/2{)}^r$。例如，如果我们的生成多项式是 $x^{14}+x^3+1$ ， 这里 $r=14$ ，那么长度 $L>15$ 的突发性差错概率是 $(1/2{)}^{14}$ ，即几乎 $16000$ 中有 $1$ 个无法被检测到。

总结如下：

• 所有 $L\le r$ 的突发性差错都会被检测到。
• 所有 $L=r+1$ 的突发性差错有 $1?(1/2{)}^{r?1}$ 的概率会被检测到。
• 所有 $L>r+1$ 的突发性差错有 $1?(1/2{)}^r$ 的概率会被检测到。

【例10.17】分析出下面与不同长度突发性差错相关的生成多项式的适用性。
a. $x^6+1$
b. $x^{18}+x^7+x+1$
c. $x^{32}+x^{23}+x^7+1$
解：

• a. 这个生成多项式，可以检测出所有长度小于或等于 $6$ 位的突发性差错，长度为 $7$ 的突发性差错无法被检测到的概率是 $3\%$ ，长度大于或等于 $8$ 的突发性差错无法被检测到的概率是 $16\%$ 。
• b. 这个生成多项式，可以检测出所有长度小于或等于 $18$ 位的突发性差错， 长度为 $19$ 的突发性差错无法被检测到的概率是百万分之 $8$ ，长度大于或等于 $20$ 的突发性差错无法被检测到的概率是百万分之 $4$ 。
• c. 这个生成多项式可以检测出所有长度小于或等于 $32$ 位的突发性差错，长度为 $33$ 的突发性差错无法被检测到的概率是千万分之 $5$ ，长度大于或等于 $34$ 的突发性差错无法被检测到的概率是千万分之 $3$ 。

5. 总结

至今为止，我们可以总结一下令人满意的生成多项式的标准。高性能生成多项式需要有以下特性：

1. 它应该至少有两项（检测单个位差错）。
2. $x^0$ 项的系数应该是 $1$（检测单个位差错）。
3. 它应该不能整除 $x^t+1$（$t$ 是 $2$ 至 $n?1$ 之间）（检测独立的双差错）。
4. 它应该有因子 $x+1$（检测奇数个差错）。

6. 标准多项式

常用协议中为CRC产生的标准多项式如表10.7所示。

10.4.5 循环编码的优点

我们已经看到循环编码在检测单个位差错、双差错、奇数个差错和突发性差错中有非常令人满意的性能。它们可以很容易地以软硬件实现。当以硬件实现时，速度尤其快，这使得循环编码成为许多网络的好选择。

10.4.6 其他循环编码

本节中讨论的循环编码很简单，校验位和校正子可以通过简单的代数计算得出。但是还有基于抽象代数的Galois域上的更强功能的多项式，它们超出了范围。这些编码中，最令人感兴趣的是目前用于检错和纠错的 Reed-Solomon 编码 Reed-Solomon code 。

10.5 校验和

这里讨论的最后一个检错方法称为校验和 checksum 。校验和在因特网中被许多不属于数据链路层的协议使用。但是，在这里简单地讨论它，以使关于检错的讨论更加完整。像线性和循环编码一样，校验和也是基于冗余的概念。将会在后面看到，许多协议仍然使用校验和进行检错，虽然趋势是它将被CRC替代。这表示CRC还用于除了数据链路层之外的其他层。

10.5.1 概念

校验和的概念并不难。让我们用几个例子来解释它。

【例10.18】假设要发送到目的地的数据是 $5$ 个 $4$ 位数字。除了发送这些数字外，我们还发送这些数字的和。例如，如果这组数字是 $(7,11,12,0,6)$ ，那么我们发送 $(7,11,12,0,6,36)$ ，这里 $36$ 是原来数字的和。接收方将这 $5$ 个数字相加、并将相加的结果与这和比较。如果两者相同，接收方就认为没差错，接收这 $5$ 个数字并丢弃和。否则，就认为有差错，不接收这个数据。

【例10.19】如果我们发送和的负值（补数）一一称为校验和，就会使接收方的工作更容易。在这个例子中，我们发送 $(7,11,12,0,6,?36)$ 。接收方将所有接收到的数字（包括校验和）相加。如果结果是 $0$ ，就认为没差错。否则就认为有差错。

10.5.2 反码

前面的例子中有一个主要的缺点。除了校验和以外，所有的数据都写做 $4$ 位字（它们小于 $15$ ）。一个解决办法是使用反码 one's complement 算法。

在这个算法中，只使用 $n$ 位表示 $0$ 到 $2^n?1$ 的无符号数字。如果这个数字多于 $n$ 位， 那么最左边的额外位要加到最右边的 $n$ 位 he extra leftmost bits need to be added to the n rightmost bits (wrapping) 。在反码算法中，一个数的负数可用该数所有位取反—— $0$ 变成 $1$ 、$1$ 变成 $0$ 表示。这与从 $2^n?1$ 减去这个数字一样。

虽然，一个数的反码可以同时代表正数和负数，但这里我们只关心无符号数。

【例10.20】在反码运算中如何只用 $4$ 位表示数字 $21$ ？
解：数字 $21$ 的二进制表示是 $10101$（需要 $5$ 位）。可以把最左边的位加到最右边的 $4$ 位上，$0101+1=0110$ 或 $6$ 。

【例10.21】在反码运算中如何只使用 $4$ 位表示数字 $?6$ ？
解：在反码算法中，一个数的负数是将所有位取反。正 $6$ 是 $0110$ ，负 $6$ 是 $1001$ 。如果只考虑无符号数字，它是 $9$ 。换言之 ，$6$ 的补数是 $9$ 。在反码运算中，另一种求一个数的反码的方法是 $2^n?1$ 减去这个数（这里是 $16?1$ ）。

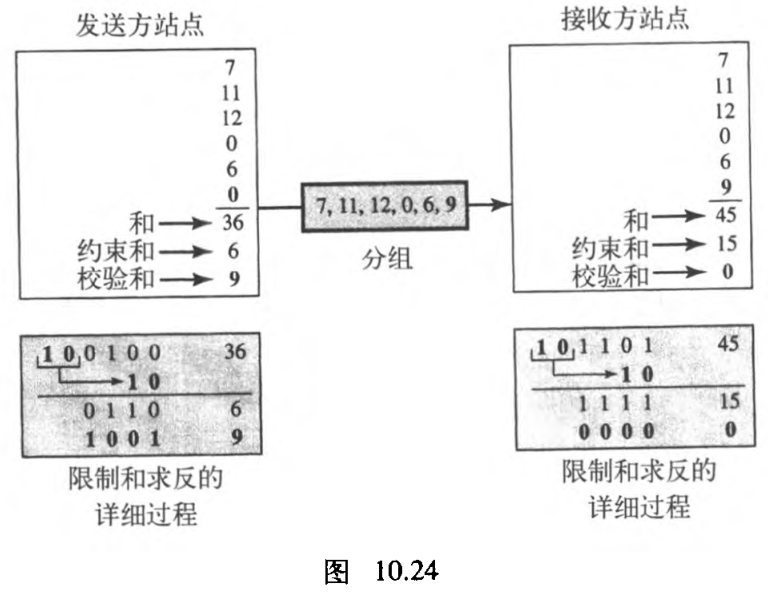
【例10.22】用反码运算重做练习10.19 。图10.24给出了发送方和接收方的处理过程。发送方先把校验和初始化为 $0$ ，并将所有数据项与校验和（校验和被看做是一个数据项，并用颜色显示）相加。其和是 $36$ 。但是，$36$ 不能用 $4$ 位表示，多出的 $2$ 位与和相加得到约束的校验和是 $6$ 。在图中，以二进制表示其详细过程。然后对和求反，结果是校验和为 $9=(15?6)$ 。

现在，发送方发送 $6$ 个数据项（包括校验和 $9$ ）给接收方。接收方执行与发送方相同的处理。它先把所有数据项相加（包括校验和） ，结果是 $45$ 。然后和变成 $15$ 。对约束和求反变成 $0$ 。因为校验和的值是 $0$ ，这表示数据没有被破坏。接收方去掉校验和，保存其他数据项。如果校验和不是 $0$ ，整个分组就被丢弃。

10.5.3 因特网校验和

传统上，因特网使用 $16$ 位校验和。发送方通过下面的步骤计算校验和。发送方站点：

1. 报文被划分为 $16$ 位字。
2. 校验和字的值设为 $0$ 。
3. 所有字包括校验和，使用反码运算相加。
4. 对这个和求反变成校验和。
5. 校验和随数据一起发送。

接收方使用如下步骤用于差错检测。接收方站点：

1. 报文（包括校验和）被划分成 $16$ 位字。
2. 用反码加法将所有字相加。
3. 对该和求反生成新的校验和。
4. 如果校验和的值是 $0$ ，接收报文；否则就丢弃报文。

校验和的特性（把字看做是数字、并相加后求反）完全适用于软件实现。可以写小程序，在接收方站点计算校验和、或检查报文的有效性。

【例10.23】让我们计算 $8$ 个字符 Forouzan 文本的校验和。该文本需要划分成 $2$ 个字节（$16$ 位）的字。使用ASCII把每个字符变成 $2$ 位十六进制数。例如，$F$ 表示成 $0x46$ ，$o$ 表示成 $0x6F$ 。图10.25说明了，如何在发送方站点和接收方站点计算校验和。在图10.25a中，第一列部分的和是 $0x36$ 。我们保持最右边的数字 $6$ ，并将最左边的数字 $3$ 作为进位插入到第二列中。每一列重复这个过程。注意，如果受到任何破坏，接收方重新计算的校验和将不全是 $0$ 。

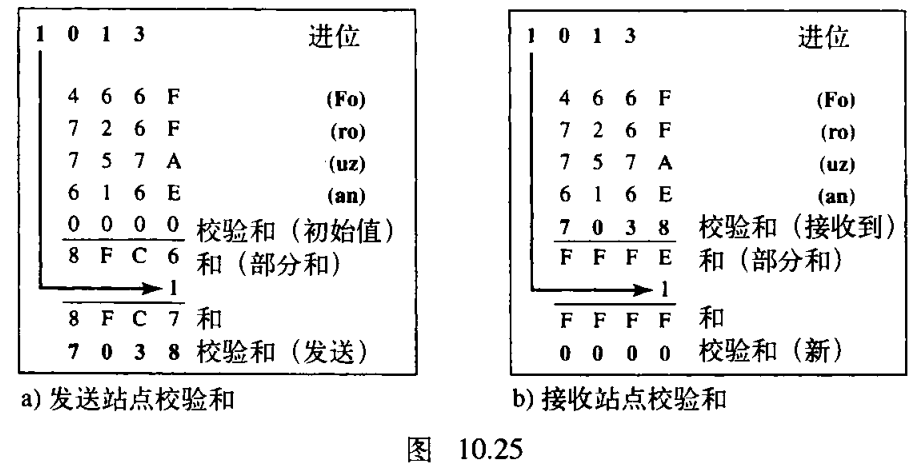
性能

传统的校验和使用较少的 $16$ 位来检测任何长度（有时是数千位）报文中的差错。但是，在差错检测能力上它没有CRC强。例如，增加一个字的值而另一个字以相同值减小，因为和以及校验和不变，所以这两个差错无法被检测到。还有，如果多个字的值增加，但是总的变化量是 $65535$ 的倍数，则和以及校验和也不变，这表示差错也无法被检测到。

Fletcher和Adler建议使用一些带权重的校验和——每个字乘以一个与「它在文本中位置」相关的一个数（称为它的权重）。这就消除了提到的第一个问题。但是因特网的趋势，尤其在新协议的设计中，是用CRC代替校验和。