题目详情如下: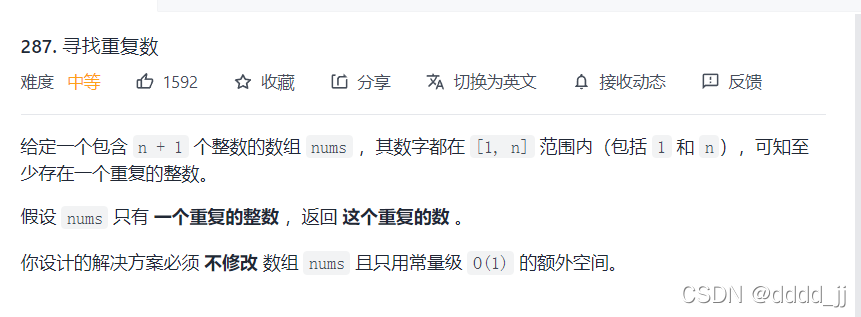
注意:题目要求不能修改数组,不能只能使用O(1)的额外空间。
方法一(使用了O(n)的空间):
定义一个map<int,int>p,遍历数组nums,遇到数组中的一个元素就去看p是否出现过了当前的元素,如果出现了,那么就直接返回当前的元素。否则就在p中标记这个元素已经出现了。
方法二(不用O(n)的空间,但是修改了数组):
因为数组长度是n+1,然后数组元素的范围是[1,n].所以可以先从数组下标为0的元素开始遍历,记录下nums[0]的值,然后跳到以nums[0]值作为下标对应的元素,判断该元素是否为-1,如果为-1,则说明nums[0]已经出现过,直接返回nums[0]。否则定义一个变量v记录nums[nums[0]]的值,然后将当前的元素修改为-1,并且跳到以v为下标的元素,再重复上面的过程。
这里举一个例子:
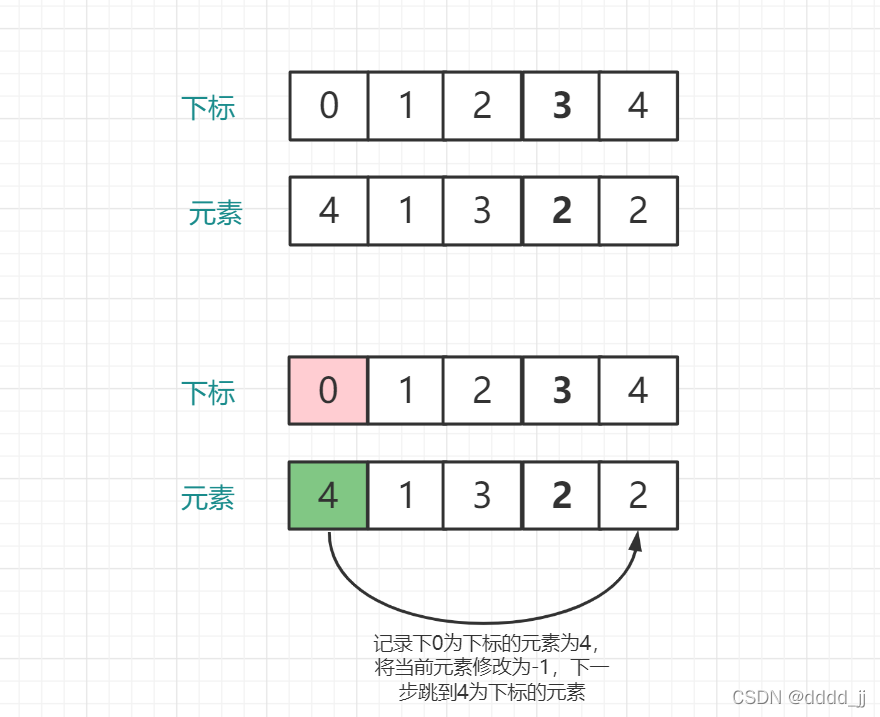
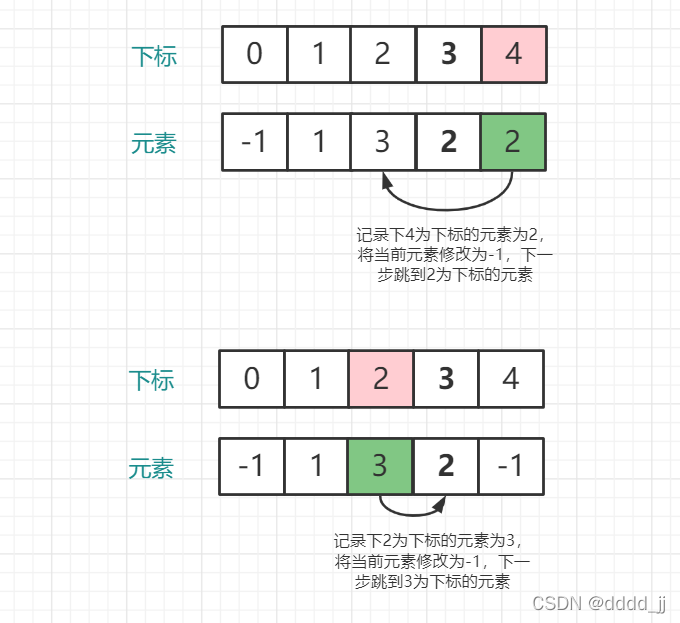
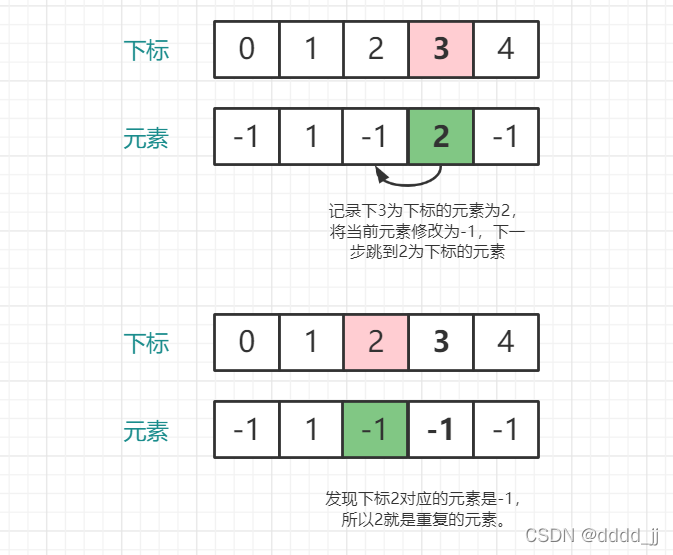
正确方法
假如方法二中的方法和例子,假设不修改数组的元素,那么数组的遍历顺序为:
4->2->3->2->3->2->3........
此时,我们可以发现,数组将进入一个环[2->3]
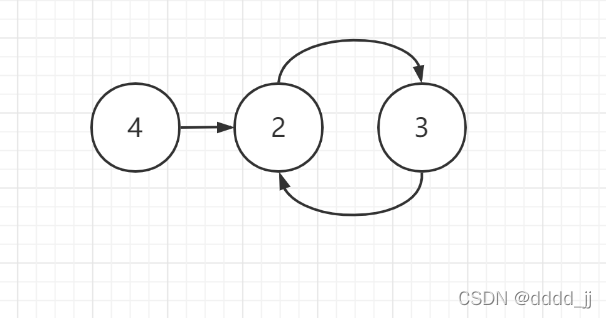
我们假设,有两个指针slow和fast,slow指针每走一步,fast指针走两步。假设slow指针走了n步,那么fast指针走了2n步,此时slow指针和fast指针在环内相遇。假设从开头到的环开头的步数为m,环内的周长为c。
那么我们可以得到slow指针在环内走了n-m步,fast指针在环内走了2n-m,fast指针在环内比slow指针多走了n步。两个指针能在环内相遇,那么fast指针比slow指针多走了几圈环,所以有n%c=0
此时我们再定义一个指针finder从开头出发,slow指针也从当前位置出发,直到两个指针相遇时,相遇的地方就是环开头的地方,也就是我们要找的重复的数,为什么呢?
当finder走到第m步时,就走到了环开头的地方。那么此时!!!!slow指针在环内走了n-m+m=n步。由于n%c=0,所以,slow指针也走到了环开头的地方。所以finder指针和slow指针会在环开头相遇。
根据上面的思路,我们有如下代码:
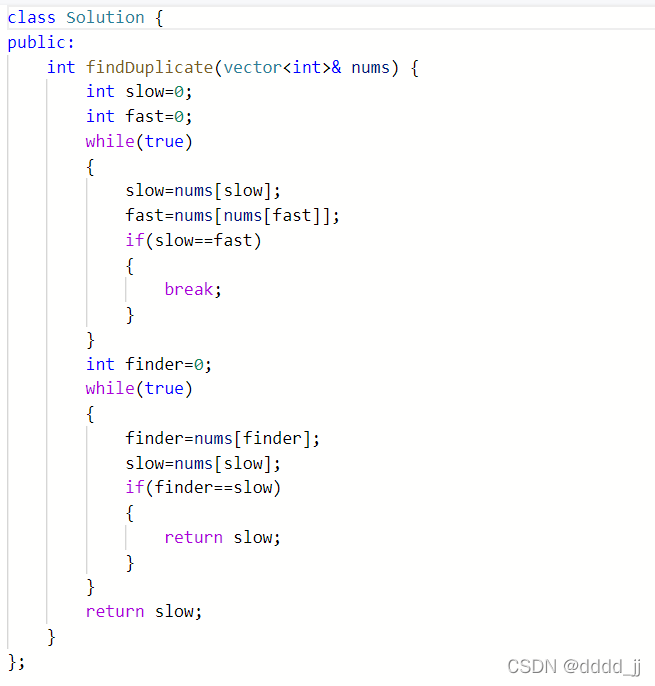
另外leetcode有类似的题目: