[数据结构与算法]东华大学oj，算法分析与实践T4斐波那契数列

题目描述

递归思想：一个数等于前两个数的和。(这并不是废话，这是执行思路)

首先分析数列的递归表达式：

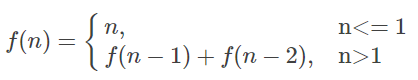
如果调用f(2)，则可知，需要计算f(1)+f(0)=1+0

因此，可以知道，f(2)=1，递归函数f(n)总共被调用3次，其中使用实参为2、为1、为0各调用一次

如果计算f(4)，则可知f(4)=f(3)+f(2)， 而f(3)=f(2)+f(1)， 继续调用，可知f(2)=f(1)+f(0)

从以上分析可知：

计算f(3)，需要调用5次f(n)

计算f(4)，需要调用9次f(n)
请使用递归方式实现本程序。

输入说明

输入一个整数n

输出说明

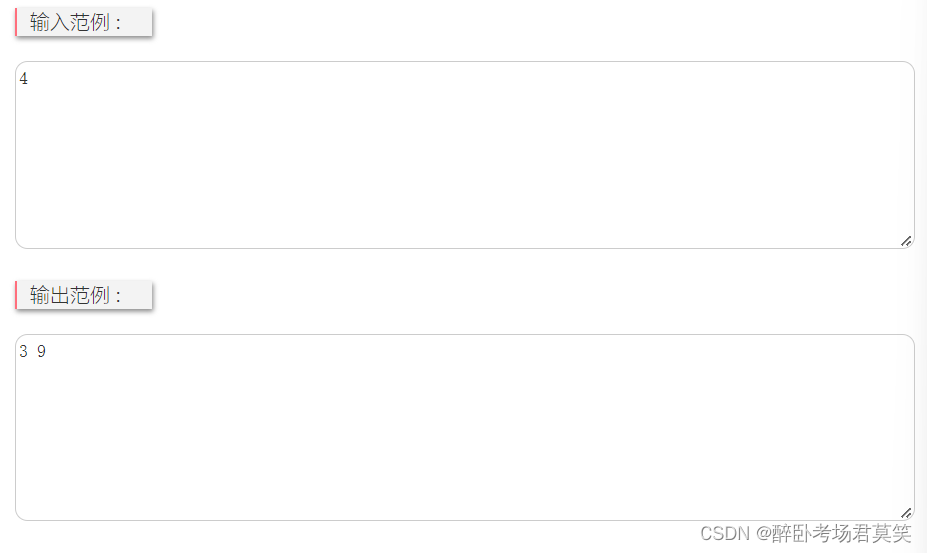
思路

观察到，求斐波那契数列的值是一个递归过程，其实求递归次数何尝不是一个递归过程，就是不只是单纯等于前面两个次数相加而已，就是再加上一个一。怎么说就是次数等于前面两个的次数相加再加一。

代码实现

代码如下（示例）：

#include <iostream>

using namespace std;
int k;
int f(int n){//求数列值
      if(n<=1){
        return n;
      } else {

      return f(n-1)+f(n-2);
      }

}
int f1(int n){//数列的次数
      if(n==1||n==0){
        return 1;
      } else {

      return (f1(n-1)+f1(n-2)+1);//我观察到，求次数其实也是一个递归过程罢了，只不过等于前面两个相加再加一
      }

}
int main()
{    int m;
     cin>>m;
     cout<<f(m)<<" "<<f1(m)<<endl;
    return 0;
}