一、问题描述
一辆卡车违反交通规则,撞人后逃跑。现场有三人目击该事件,但都没有记住车号,只记下了车号的一些特征。甲说:牌照的前两位数字是相同的;乙说:牌照的后两位数字是相同的,但与前两位不同;丙是数学家,他说:4位的车号刚好是一个整数的平方。请根据以上线索求出车号。
二、问题分析
按照题目的要求造出一个前两位数相同、后两位数相同且相互间又不同的4位整数,然后判断该整数是否是另一个整数的平方。即求一个4位数 a1a2a3a4,满足如下条件:
y
=
{
a
1
=
a
2
,
1
≤
a
1
,
a
2
≤
9
a
3
=
a
4
,
0
≤
a
3
,
a
4
≤
9
a
1
≠
a
3
1000
×
a
1
+
100
×
a
2
+
10
×
a
3
+
a
4
=
x
2
,
x
∈
Z
y= \begin{cases} a_1=a_2,\quad 1\leq a_1,a_2\leq9\\ a_3=a_4, \quad 0\leq a_3,a_4\leq9\\ a_1\neq a_3\\ 1000×a_1+100×a_2+10×a_3+a_4 = x^2, x\in Z \end{cases}
y=??????????a1?=a2?,1≤a1?,a2?≤9a3?=a4?,0≤a3?,a4?≤9a1??=a3?1000×a1?+100×a2?+10×a3?+a4?=x2,x∈Z?
三、算法设计
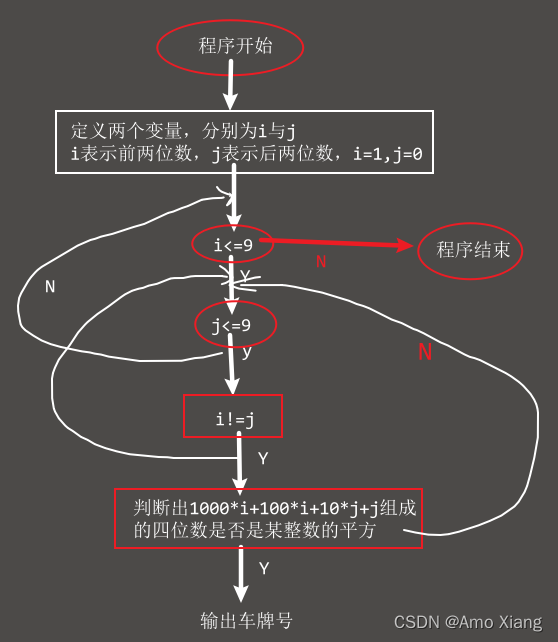
本练习是数值计算问题,求解不定方程。对于这种求解不定方程组的问题,一般采用穷举循环,首先设计双层循环 (需要根据实际情况思考几层循环)穷举出所有由前两位数和后两位数组成的4位数车牌,然后在最内层穷举出所有平方后值为4位数并且小于车牌号的数,判断该数是否与车牌相等,若相等,则打印车牌。
四、确定程序框架
程序流程图如下图所示 (简陋,见笑见笑):
五、视频讲解
晚上回去补
六、示例代码
# -*- coding: utf-8 -*-
# @Time : 2022/2/23 23:45
# @Author : AmoXiang
# @FileName: 1.抓交通肇事犯.py
# @Software: PyCharm
# @Blog :https://blog.csdn.net/xw1680?
# TODO 1.定义变量
# i代表前两位车牌号数字,j代表后两位车牌号的数字,lic_pla_num代表车牌号
flag = False # 循环标识变量(开关),为True时退出所有循环
for i in range(1, 10):
if flag:
break
for j in range(0, 10): # 穷举前两位和后两位车牌数字
if flag:
break
# TODO 2.判断前两位和后两位数字是否相同(即判断i和j)
if i != j:
# TODO 3.组成4位车牌号码
lic_pla_num = 1000 * i + 100 * i + 10 * j + j
# TODO 4.判断_是否是某个数的平方,是就输出
for _ in range(31, 100):
if _ ** 2 == lic_pla_num:
flag = True
print(f"车牌号为: {lic_pla_num}")
break
运行结果如下图所示:
七、课后练习
练习:有四个数字:1、2、3、4,能组成多少个互不相同且无重复数字的三位数?各是多少?