一、连续,偏导数不一定存在
这个很容易理解,跟一元函数一样。
例如
f
(
x
,
y
)
=
∣
x
∣
f(x,y)=|x|
f(x,y)=∣x∣,在
(
0
,
0
)
(0,0)
(0,0)连续,但
f
x
(
0
,
0
)
=
d
∣
x
∣
d
x
f_x(0,0)=\frac{\text{d}|x|}{\text{d}x}
fx?(0,0)=dxd∣x∣?不存在。
再例如,
f
(
x
,
y
)
=
x
2
+
y
2
f(x,y)=\sqrt{x^2+y^2}
f(x,y)=x2+y2?,其在
(
0
,
0
)
(0,0)
(0,0)点显然连续,但
f
x
(
0
,
0
)
=
lim
?
x
→
0
∣
x
∣
x
f_x(0,0)=\lim_{x\to0}\frac{|x|}{x}
fx?(0,0)=x→0lim?x∣x∣?不存在,
f
y
(
0
,
0
)
f_y(0,0)
fy?(0,0)同理也不存在。
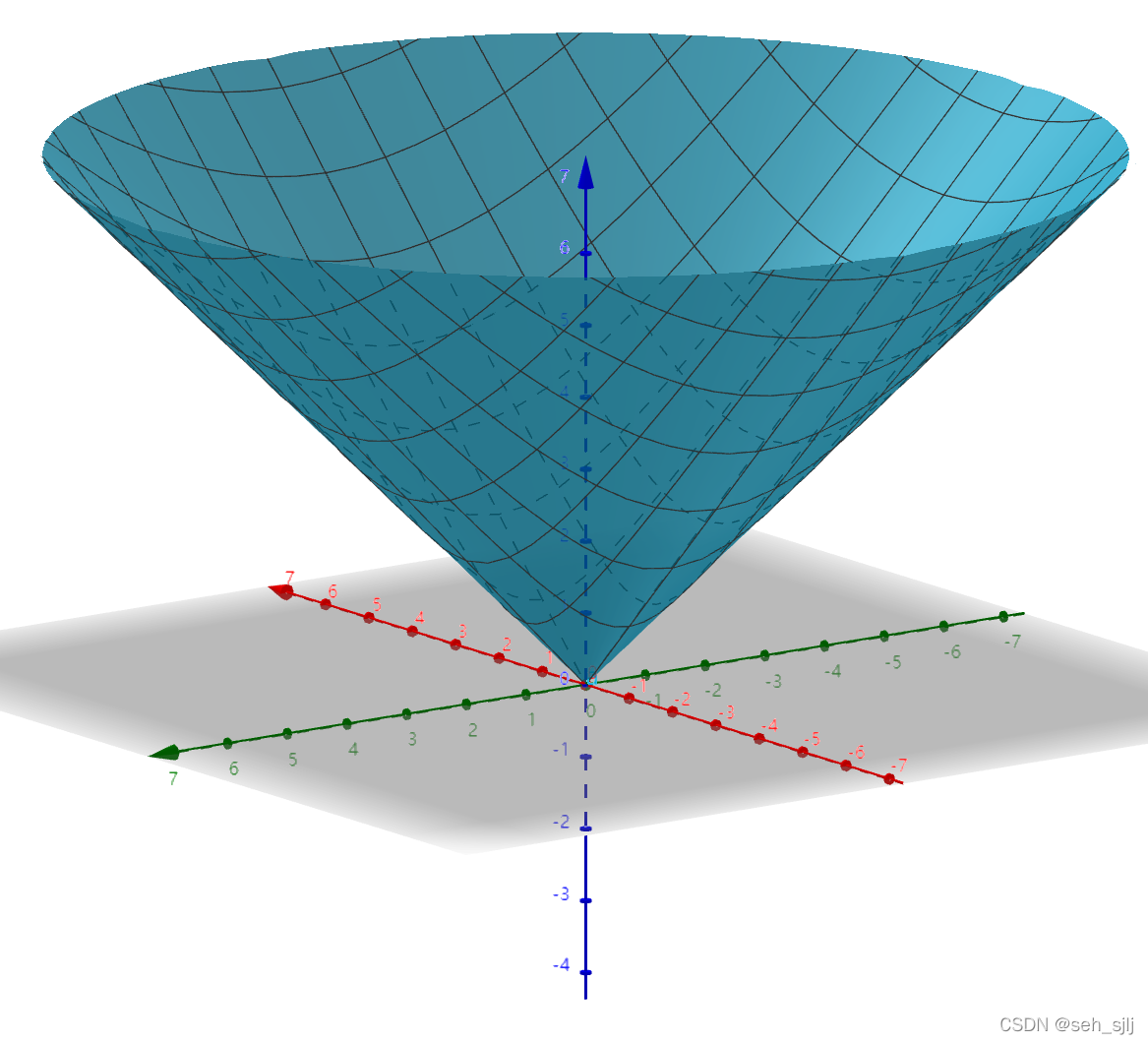
用Geogebra画图可以看出这个函数的图像是锥形,在
(
0
,
0
)
(0,0)
(0,0)点是尖的:
二、偏导数存在,不一定连续
这个性质跟一元函数有很大差异。对于二元函数,偏导数存在是很弱的条件,甚至连极限都有可能不存在。
例子:
f
(
x
,
y
)
=
{
x
y
x
2
+
y
2
,
x
2
+
y
2
≠
0
0
,
x
2
+
y
2
=
0
f(x,y)=\begin{cases}\frac{xy}{x^2+y^2},&x^2+y^2\ne0\\0,&x^2+y^2=0\end{cases}
f(x,y)={x2+y2xy?,0,?x2+y2?=0x2+y2=0?它在
(
0
,
0
)
(0,0)
(0,0)点的两个偏导数都存在:
f
x
(
0
,
0
)
=
f
y
(
0
,
0
)
=
0
f_x(0,0)=f_y(0,0)=0
fx?(0,0)=fy?(0,0)=0但是它在
(
0
,
0
)
(0,0)
(0,0)点的极限不存在,以
y
=
k
x
y=kx
y=kx的路径逼近
(
0
,
0
)
(0,0)
(0,0)得
lim
?
x
→
0
,
y
=
k
x
x
y
x
2
+
y
2
=
k
1
+
k
2
\lim_{x\to0,y=kx}\frac{xy}{x^2+y^2}=\frac{k}{1+k^2}
x→0,y=kxlim?x2+y2xy?=1+k2k?随着
k
k
k的变化而变化,所以
lim
?
(
x
,
y
)
→
(
0
,
0
)
f
(
x
,
y
)
\lim_{(x,y)\to(0,0)}f(x,y)
(x,y)→(0,0)lim?f(x,y)不存在。
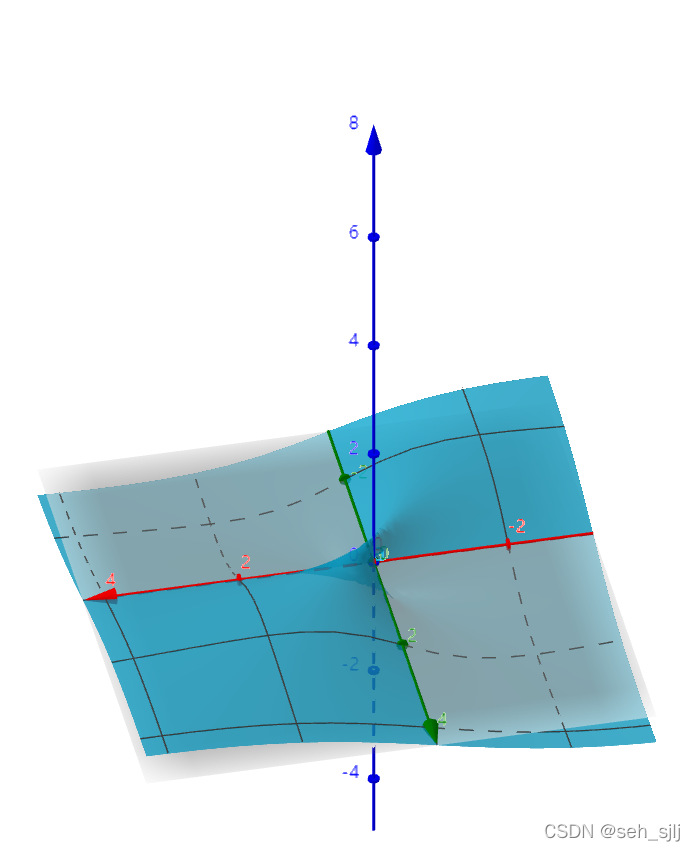
画图看出这个函数在
(
0
,
0
)
(0,0)
(0,0)点呈现一个很奇怪的样子:
三、可微,一定连续、偏导数存在
定理1(可微的必要条件) 设函数
z
=
f
(
x
,
y
)
z=f(x,y)
z=f(x,y)在
(
x
0
,
y
0
)
(x_0,y_0)
(x0?,y0?)处可微,则
(1)
f
f
f在
(
x
0
,
y
0
)
(x_0,y_0)
(x0?,y0?)处连续;
(2)
f
f
f在
(
x
0
,
y
0
)
(x_0,y_0)
(x0?,y0?)处的两个偏导数都存在,且有
d
f
(
x
0
,
y
0
)
=
f
x
(
x
0
,
y
0
)
d
x
+
f
y
(
x
0
,
y
0
)
d
y
\text{d}f(x_0,y_0)=f_x(x_0,y_0)\text{d}x+f_y(x_0,y_0)\text{d}y
df(x0?,y0?)=fx?(x0?,y0?)dx+fy?(x0?,y0?)dy。
证明:
(1) 当
f
f
f在
(
x
0
,
y
0
)
(x_0,y_0)
(x0?,y0?)处可微时,存在常数
a
1
,
a
2
a_1,a_2
a1?,a2?使得
Δ
z
=
a
1
Δ
x
+
a
2
Δ
y
+
o
(
ρ
)
\Delta z=a_1\Delta x+a_2\Delta y+o(\rho)
Δz=a1?Δx+a2?Δy+o(ρ),其中
ρ
=
(
Δ
x
)
2
+
(
Δ
y
)
2
\rho=\sqrt{(\Delta x)^2+(\Delta y)^2}
ρ=(Δx)2+(Δy)2?。令
ρ
→
0
\rho\to0
ρ→0,即
Δ
x
→
0
\Delta x\to0
Δx→0且
Δ
y
→
0
\Delta y\to0
Δy→0,得
lim
?
ρ
→
0
Δ
z
=
0
\lim_{\rho\to0}\Delta z=0
ρ→0lim?Δz=0或
lim
?
Δ
x
→
0
,
Δ
y
→
0
f
(
x
0
+
Δ
x
,
y
0
+
Δ
y
)
=
lim
?
Δ
x
→
0
,
Δ
y
→
0
[
f
(
x
0
,
y
0
)
+
Δ
z
]
=
f
(
x
0
,
y
0
)
\lim_{\Delta x\to0,\Delta y\to0}f(x_0+\Delta x,y_0+\Delta y)=\lim_{\Delta x\to0,\Delta y\to0}[f(x_0,y_0)+\Delta z]=f(x_0,y_0)
Δx→0,Δy→0lim?f(x0?+Δx,y0?+Δy)=Δx→0,Δy→0lim?[f(x0?,y0?)+Δz]=f(x0?,y0?)因此
f
f
f在
(
x
0
,
y
0
)
(x_0,y_0)
(x0?,y0?)处连续。
(2) 由可微的定义,
f
f
f满足
f
(
x
0
+
Δ
x
,
y
0
+
Δ
y
)
?
f
(
x
0
,
y
0
)
=
a
1
Δ
x
+
a
2
Δ
y
+
o
(
ρ
)
f(x_0+\Delta x,y_0+\Delta y)-f(x_0,y_0)=a_1\Delta x+a_2\Delta y+o(\rho)
f(x0?+Δx,y0?+Δy)?f(x0?,y0?)=a1?Δx+a2?Δy+o(ρ)取
Δ
y
=
0
\Delta y=0
Δy=0,则有
ρ
=
∣
Δ
x
∣
\rho=|\Delta x|
ρ=∣Δx∣,上式变为
f
(
x
0
+
Δ
x
,
y
0
)
?
f
(
x
0
,
y
0
)
=
a
1
+
o
(
∣
Δ
x
∣
)
f(x_0+\Delta x,y_0)-f(x_0,y_0)=a_1+o(|\Delta x|)
f(x0?+Δx,y0?)?f(x0?,y0?)=a1?+o(∣Δx∣)两边除以
Δ
x
\Delta x
Δx并取极限得
lim
?
Δ
x
→
0
f
(
x
0
+
Δ
x
,
y
0
)
?
f
(
x
0
,
y
0
)
Δ
x
=
lim
?
Δ
x
→
0
[
a
1
+
o
(
∣
Δ
x
∣
)
Δ
x
]
=
a
1
\lim_{\Delta x\to0}\frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x}=\lim_{\Delta x\to0}\left[a_1+\frac{o(|\Delta x|)}{\Delta x}\right]=a_1
Δx→0lim?Δxf(x0?+Δx,y0?)?f(x0?,y0?)?=Δx→0lim?[a1?+Δxo(∣Δx∣)?]=a1?即
f
x
(
x
0
,
y
0
)
=
a
1
f_x(x_0,y_0)=a_1
fx?(x0?,y0?)=a1?。
同理,取
Δ
x
=
0
\Delta x=0
Δx=0得
f
y
(
x
0
,
y
0
)
=
a
2
f_y(x_0,y_0)=a_2
fy?(x0?,y0?)=a2?。?
从这里我们可以看出,可微是很强得条件,远比偏导数存在要强。
然而,这个条件仅仅是必要条件。我们举一个例子
f
(
x
,
y
)
=
{
x
y
x
2
+
y
2
,
x
2
+
y
2
≠
0
0
,
x
2
+
y
2
=
0
f(x,y)=\begin{cases}\frac{xy}{\sqrt{x^2+y^2}},&x^2+y^2\ne0\\0,&x^2+y^2=0\end{cases}
f(x,y)={x2+y2?xy?,0,?x2+y2?=0x2+y2=0?它在
(
0
,
0
)
(0,0)
(0,0)点连续,因为
lim
?
(
x
,
y
)
→
(
0
,
0
)
∣
f
(
x
,
y
)
?
f
(
0
,
0
)
∣
=
lim
?
(
x
,
y
)
→
(
0
,
0
)
∣
f
(
x
,
y
)
∣
≤
lim
?
(
x
,
y
)
→
(
0
,
0
)
x
2
+
y
2
2
x
2
+
y
2
=
0
\lim_{(x,y)\to(0,0)}|f(x,y)-f(0,0)|=\lim_{(x,y)\to(0,0)}|f(x,y)|\le\lim_{(x,y)\to(0,0)}\frac{x^2+y^2}{2\sqrt{x^2+y^2}}=0
(x,y)→(0,0)lim?∣f(x,y)?f(0,0)∣=(x,y)→(0,0)lim?∣f(x,y)∣≤(x,y)→(0,0)lim?2x2+y2?x2+y2?=0两个偏导数也存在:
f
x
(
0
,
0
)
=
f
y
(
0
,
0
)
=
0
f_x(0,0)=f_y(0,0)=0
fx?(0,0)=fy?(0,0)=0但不可微。因为如果可微,那么
Δ
f
?
f
x
(
0
,
0
)
Δ
x
?
f
y
(
0
,
0
)
Δ
y
=
o
(
ρ
)
\Delta f-f_x(0,0)\Delta x-f_y(0,0)\Delta y=o(\rho)
Δf?fx?(0,0)Δx?fy?(0,0)Δy=o(ρ)。然而
lim
?
(
x
,
y
)
→
(
0
,
0
)
Δ
f
ρ
=
lim
?
(
x
,
y
)
→
(
0
,
0
)
x
y
x
2
+
y
2
\lim_{(x,y)\to(0,0)}\frac{\Delta f}{\rho}=\lim_{(x,y)\to(0,0)}\frac{xy}{x^2+y^2}
(x,y)→(0,0)lim?ρΔf?=(x,y)→(0,0)lim?x2+y2xy?不存在。也就是说,满足定理1的条件不一定可微。
其函数图像如下:

四、偏导数连续,一定可微
定理2(可微的充分条件) 设函数
z
=
f
(
x
,
y
)
z=f(x,y)
z=f(x,y)在点
(
x
0
,
y
0
)
(x_0,y_0)
(x0?,y0?)得的某个邻域内有定义,若
f
(
x
,
y
)
f(x,y)
f(x,y)的两个偏导数均在点
(
x
0
,
y
0
)
(x_0,y_0)
(x0?,y0?)处连续,则该函数在点
(
x
0
,
y
0
)
(x_0,y_0)
(x0?,y0?)处可微。
证明:
Δ
z
=
f
(
x
0
+
Δ
x
,
y
0
+
Δ
y
)
?
f
(
x
0
,
y
0
)
=
[
f
(
x
0
+
Δ
x
,
y
0
+
Δ
y
)
?
f
(
x
0
,
y
0
+
Δ
y
)
]
+
[
f
(
x
0
,
y
0
+
Δ
y
)
?
f
(
x
0
,
y
0
)
]
\begin{aligned}\Delta z&=f(x_0+\Delta x,y_0+\Delta y)-f(x_0,y_0)\\&=[f(x_0+\Delta x,y_0+\Delta y)-f(x_0,y_0+\Delta y)]+[f(x_0,y_0+\Delta y)-f(x_0,y_0)]\end{aligned}
Δz?=f(x0?+Δx,y0?+Δy)?f(x0?,y0?)=[f(x0?+Δx,y0?+Δy)?f(x0?,y0?+Δy)]+[f(x0?,y0?+Δy)?f(x0?,y0?)]?右边的每一项都是一元函数的改变量,故可以采用拉格朗日中值定理(
f
(
b
)
?
f
(
a
)
=
f
′
(
ξ
)
(
b
?
a
)
f(b)-f(a)=f'(\xi)(b-a)
f(b)?f(a)=f′(ξ)(b?a)),即存在
θ
1
,
θ
2
∈
(
0
,
1
)
\theta_1,\theta_2\in(0,1)
θ1?,θ2?∈(0,1)使得
Δ
z
=
f
x
(
x
0
+
θ
1
Δ
x
,
y
0
+
Δ
y
)
Δ
x
+
f
y
(
x
0
,
y
0
+
θ
2
Δ
y
)
Δ
y
\Delta z=f_x(x_0+\theta_1\Delta x,y_0+\Delta y)\Delta x+f_y(x_0,y_0+\theta_2\Delta y)\Delta y
Δz=fx?(x0?+θ1?Δx,y0?+Δy)Δx+fy?(x0?,y0?+θ2?Δy)Δy由于
f
x
(
x
,
y
)
f_x(x,y)
fx?(x,y)在
(
x
0
,
y
0
)
(x_0,y_0)
(x0?,y0?)连续,取极限
ρ
=
(
Δ
x
)
2
+
(
Δ
y
)
2
→
0
\rho=\sqrt{(\Delta x)^2+(\Delta y)^2}\to0
ρ=(Δx)2+(Δy)2?→0得
lim
?
ρ
→
0
f
x
(
x
0
+
θ
1
Δ
x
,
y
0
+
Δ
y
)
=
f
x
(
x
0
,
y
0
)
\lim_{\rho\to0}f_x(x_0+\theta_1\Delta x,y_0+\Delta y)=f_x(x_0,y_0)
ρ→0lim?fx?(x0?+θ1?Δx,y0?+Δy)=fx?(x0?,y0?)因此有
f
x
(
x
0
+
θ
1
Δ
x
,
y
0
+
Δ
y
)
=
f
x
(
x
0
,
y
0
)
+
α
1
(
ρ
)
f_x(x_0+\theta_1\Delta x,y_0+\Delta y)=f_x(x_0,y_0)+\alpha_1(\rho)
fx?(x0?+θ1?Δx,y0?+Δy)=fx?(x0?,y0?)+α1?(ρ)同理有
f
y
(
x
0
,
y
0
+
θ
2
Δ
y
)
=
f
(
x
0
,
y
0
)
+
α
2
(
ρ
)
f_y(x_0,y_0+\theta_2\Delta y)=f(x_0,y_0)+\alpha_2(\rho)
fy?(x0?,y0?+θ2?Δy)=f(x0?,y0?)+α2?(ρ)其中
α
1
,
2
(
ρ
)
\alpha_{1,2}( \rho)
α1,2?(ρ)是
ρ
\rho
ρ的高阶无穷小。整理得
Δ
z
=
f
(
x
0
+
Δ
x
,
y
0
+
Δ
y
)
?
f
(
x
0
,
y
0
)
=
[
f
(
x
0
+
Δ
x
,
y
0
+
Δ
y
)
?
f
(
x
0
,
y
0
+
Δ
y
)
]
+
[
f
(
x
0
,
y
0
+
Δ
y
)
?
f
(
x
0
,
y
0
)
]
=
[
f
x
(
x
0
,
y
0
)
+
α
1
(
ρ
)
]
Δ
x
+
[
f
(
x
0
,
y
0
)
+
α
2
(
ρ
)
]
Δ
y
=
f
x
(
x
0
,
y
0
)
Δ
x
+
f
y
(
x
0
,
y
0
)
Δ
y
+
α
1
(
ρ
)
Δ
x
+
α
2
(
ρ
)
Δ
y
\begin{aligned}\Delta z&=f(x_0+\Delta x,y_0+\Delta y)-f(x_0,y_0)\\&=[f(x_0+\Delta x,y_0+\Delta y)-f(x_0,y_0+\Delta y)]+[f(x_0,y_0+\Delta y)-f(x_0,y_0)]\\&=[f_x(x_0,y_0)+\alpha_1(\rho)]\Delta x+[f(x_0,y_0)+\alpha_2(\rho)]\Delta y\\&=f_x(x_0,y_0)\Delta x+f_y(x_0,y_0)\Delta y+\alpha_1(\rho)\Delta x+\alpha_2(\rho)\Delta y\end{aligned}
Δz?=f(x0?+Δx,y0?+Δy)?f(x0?,y0?)=[f(x0?+Δx,y0?+Δy)?f(x0?,y0?+Δy)]+[f(x0?,y0?+Δy)?f(x0?,y0?)]=[fx?(x0?,y0?)+α1?(ρ)]Δx+[f(x0?,y0?)+α2?(ρ)]Δy=fx?(x0?,y0?)Δx+fy?(x0?,y0?)Δy+α1?(ρ)Δx+α2?(ρ)Δy?只需证明后面两项是
ρ
\rho
ρ的高阶无穷小。而
Δ
x
≤
ρ
\Delta x\le\rho
Δx≤ρ,
Δ
y
≤
ρ
\Delta y\le\rho
Δy≤ρ,所以
∣
α
1
(
ρ
)
Δ
x
+
α
2
(
ρ
)
Δ
y
∣
≤
∣
α
1
(
ρ
)
+
α
2
(
ρ
)
∣
ρ
|\alpha_1(\rho)\Delta x+\alpha_2(\rho)\Delta y|\le|\alpha_1(\rho)+\alpha_2(\rho)|\rho
∣α1?(ρ)Δx+α2?(ρ)Δy∣≤∣α1?(ρ)+α2?(ρ)∣ρ,
lim
?
ρ
→
0
∣
α
1
(
ρ
)
Δ
x
+
α
2
(
ρ
)
Δ
y
ρ
∣
=
lim
?
ρ
→
0
α
1
(
ρ
)
+
α
2
(
ρ
)
=
o
(
ρ
)
\lim_{\rho\to0}\left|\frac{\alpha_1(\rho)\Delta x+\alpha_2(\rho)\Delta y}{\rho}\right|=\lim_{\rho\to0}\alpha_1(\rho)+\alpha_2(\rho)=o(\rho)
ρ→0lim?∣∣∣∣?ρα1?(ρ)Δx+α2?(ρ)Δy?∣∣∣∣?=ρ→0lim?α1?(ρ)+α2?(ρ)=o(ρ)于是
α
1
(
ρ
)
Δ
x
+
α
2
(
ρ
)
Δ
y
\alpha_1(\rho)\Delta x+\alpha_2(\rho)\Delta y
α1?(ρ)Δx+α2?(ρ)Δy是
ρ
\rho
ρ的高阶无穷小。因此有
Δ
z
=
f
x
(
x
0
,
y
0
)
Δ
x
+
f
y
(
x
0
,
y
0
)
Δ
y
+
o
(
ρ
)
\Delta z=f_x(x_0,y_0)\Delta x+f_y(x_0,y_0)\Delta y+o(\rho)
Δz=fx?(x0?,y0?)Δx+fy?(x0?,y0?)Δy+o(ρ)即
f
f
f在
(
x
0
,
y
0
)
(x_0,y_0)
(x0?,y0?)处可微。?
注意:这只是充分条件。有些函数,例如 f ( x , y ) = { ( x 2 + y 2 ) sin ? 1 x 2 + y 2 , x 2 + y 2 ≠ 0 0 , x 2 + y 2 = 0 f(x,y)=\begin{cases}(x^2+y^2)\sin{\frac{1}{x^2+y^2}},&x^2+y^2\ne0\\0,&x^2+y^2=0\end{cases} f(x,y)={(x2+y2)sinx2+y21?,0,?x2+y2?=0x2+y2=0?它在 ( 0 , 0 ) (0,0) (0,0)处可微,但 f x ( x , y ) f_x(x,y) fx?(x,y)与 f y ( x , y ) f_y(x,y) fy?(x,y)在 ( 0 , 0 ) (0,0) (0,0)处间断。
五、偏导数连续,函数一定连续
这是定理1和定理2结合起来后一个很显然的推论。
六、可微,则沿任一方向的方向导数存在
定理3 若
f
(
x
,
y
)
f(x,y)
f(x,y)在点
(
x
0
,
y
0
)
(x_0,y_0)
(x0?,y0?)可微,则函数
f
f
f在点
(
x
0
,
y
0
)
(x_0,y_0)
(x0?,y0?)沿任意
l
\bm l
l方向的方向导数均存在,且
?
f
?
l
∣
x
0
,
y
0
=
f
x
(
x
0
,
y
0
)
cos
?
α
+
f
y
(
x
0
,
y
0
)
cos
?
β
\left.\frac{\partial f}{\partial\bm l}\right|_{x_0,y_0}=f_x(x_0,y_0)\cos\alpha+f_y(x_0,y_0)\cos\beta
?l?f?∣∣∣∣?x0?,y0??=fx?(x0?,y0?)cosα+fy?(x0?,y0?)cosβ其中
l
\bm l
l方向上的单位向量是
e
l
=
(
cos
?
α
,
cos
?
β
)
\bm e_l=(\cos\alpha,\cos\beta)
el?=(cosα,cosβ)。
证明:由定理1,当
(
x
,
y
)
→
(
0
,
0
)
(x,y)\to(0,0)
(x,y)→(0,0)时,有
f
(
x
,
y
)
?
f
(
x
0
,
y
0
)
=
f
x
(
x
0
,
y
0
)
Δ
x
+
f
y
(
x
0
,
y
0
)
Δ
y
+
o
(
ρ
)
f(x,y)-f(x_0,y_0)=f_x(x_0,y_0)\Delta x+f_y(x_0,y_0)\Delta y+o(\rho)
f(x,y)?f(x0?,y0?)=fx?(x0?,y0?)Δx+fy?(x0?,y0?)Δy+o(ρ)令
(
x
,
y
)
=
(
x
0
,
y
0
)
+
t
e
l
=
(
x
0
,
y
0
)
+
(
t
cos
?
α
,
t
cos
?
β
)
(x,y)=(x_0,y_0)+t\bm e_l=(x_0,y_0)+(t\cos\alpha,t\cos\beta)
(x,y)=(x0?,y0?)+tel?=(x0?,y0?)+(tcosα,tcosβ),即
Δ
x
=
t
cos
?
α
,
Δ
y
=
t
cos
?
β
,
∣
t
∣
=
(
Δ
x
)
2
+
(
Δ
y
)
2
\Delta x=t\cos\alpha,\Delta y=t\cos\beta,|t|=\sqrt{(\Delta x)^2+(\Delta y)^2}
Δx=tcosα,Δy=tcosβ,∣t∣=(Δx)2+(Δy)2?,可得
f
(
x
0
,
y
0
)
=
f
x
(
x
0
,
y
0
)
t
cos
?
α
+
f
y
(
x
0
,
y
0
)
t
cos
?
β
+
o
(
ρ
)
f(x_0,y_0)=f_x(x_0,y_0)t\cos\alpha+f_y(x_0,y_0)t\cos\beta+o(\rho)
f(x0?,y0?)=fx?(x0?,y0?)tcosα+fy?(x0?,y0?)tcosβ+o(ρ)由方向导数的定义有
?
f
?
l
∣
x
0
,
y
0
=
lim
?
t
→
0
f
(
x
0
+
t
cos
?
α
,
y
0
+
t
cos
?
β
)
?
f
(
x
0
,
y
0
)
t
=
lim
?
t
→
0
f
x
(
x
0
,
y
0
)
t
cos
?
α
+
f
y
(
x
0
,
y
0
)
t
cos
?
β
+
o
(
∣
t
∣
)
t
=
f
x
(
x
0
,
y
0
)
cos
?
α
+
f
y
(
x
0
,
y
0
)
cos
?
β
\begin{aligned}\left.\frac{\partial f}{\partial\bm l}\right|_{x_0,y_0}&=\lim_{t\to0}\frac{f(x_0+t\cos\alpha,y_0+t\cos\beta)-f(x_0,y_0)}{t}\\&=\lim_{t\to0}\frac{f_x(x_0,y_0)t\cos\alpha+f_y(x_0,y_0)t\cos\beta+o(|t|)}{t}\\&=f_x(x_0,y_0)\cos\alpha+f_y(x_0,y_0)\cos\beta\end{aligned}
?l?f?∣∣∣∣?x0?,y0???=t→0lim?tf(x0?+tcosα,y0?+tcosβ)?f(x0?,y0?)?=t→0lim?tfx?(x0?,y0?)tcosα+fy?(x0?,y0?)tcosβ+o(∣t∣)?=fx?(x0?,y0?)cosα+fy?(x0?,y0?)cosβ?证毕。?
综合以上所有讨论,得到下面这张图:
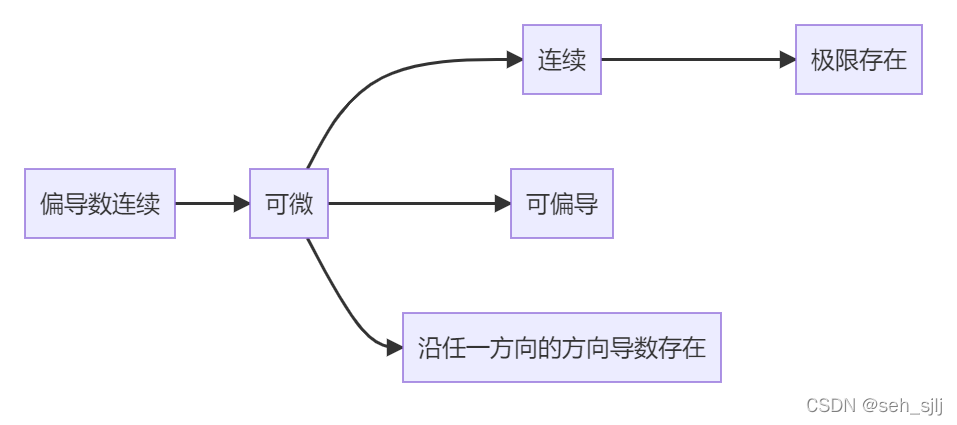
可以看出偏导数连续是最强的条件,可微是很强的条件,(任意方向)偏导数存在是很弱的条件。