文章目录
拉普拉斯变换及其性质
傅里叶变换:
j
w
jw
jw
拉普拉斯变换:
s
=
σ
+
j
w
s=\sigma+jw
s=σ+jw
1 双边拉普拉斯变换的定义
有些函数不满足绝对可积条件,求解傅里叶变换困难。为此,可用一衰减因子 e ? σ t e^{-\sigma t} e?σt( σ \sigma σ为实常数)乘信号 f ( t ) f(t) f(t),适当选取 σ \sigma σ的值,使乘积信号 f ( t ) e ? σ t f(t)e^{-\sigma t} f(t)e?σt当 t → ∞ t\rightarrow \infty t→∞时信号幅度趋近于0 ,从而使 f ( t ) e ? σ t f(t)e^{-\sigma t} f(t)e?σt的傅里叶变换存在。
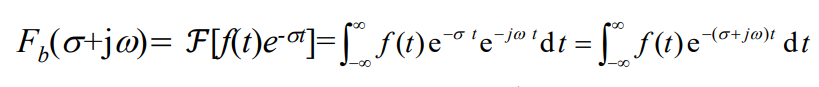
相应的傅里叶逆变换为:
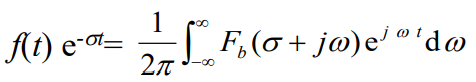
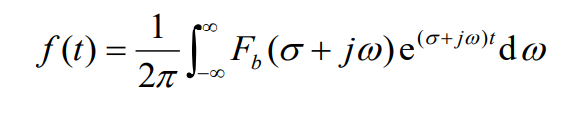

2 收敛域
只有选择适当的 σ \sigma σ值才能使积分收敛,信号 f ( t ) f(t) f(t)的双边拉普拉斯变换存在。
收敛域:使 f ( t ) f(t) f(t) 拉氏变换存在的 σ \sigma σ取值范围。
2.1 因果信号
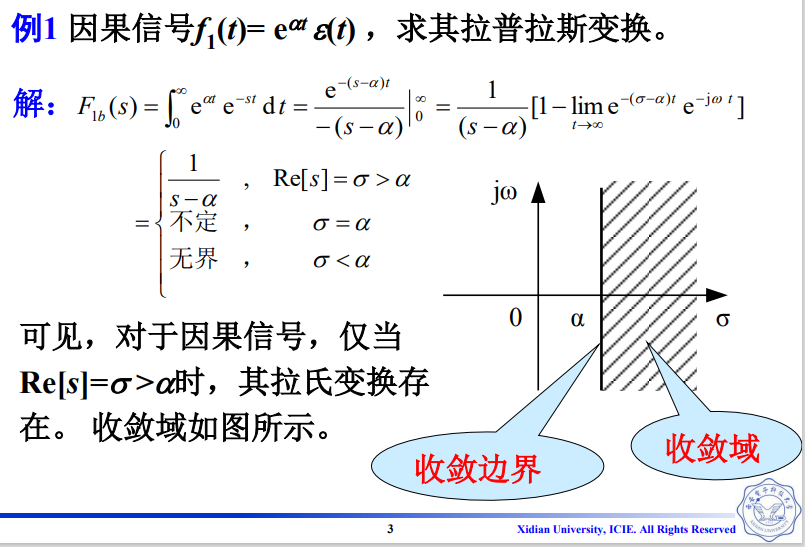
因果信号的收敛域在某一条直线之右。
2.2 反因果信号
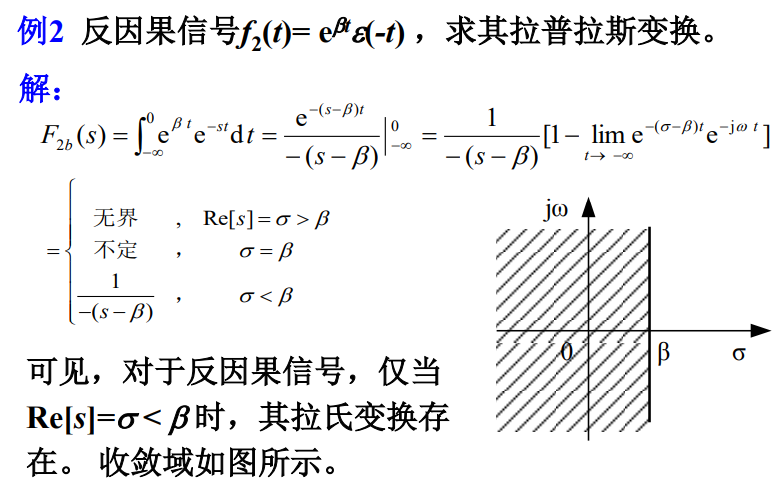
反因果信号的收敛域在某一条直线之左。
2.3 双边信号
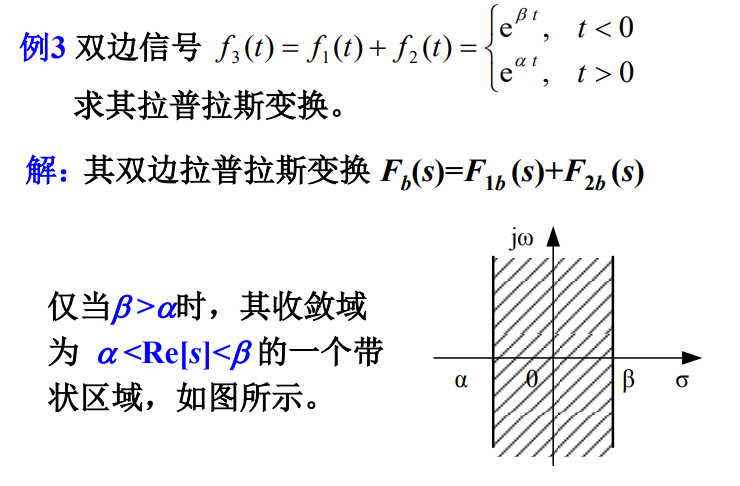
双边信号的收敛域在两条直线之间。

结论:
(1) 对于双边拉普拉斯变换而言, F b ( s ) F_b(s) Fb?(s)和收敛域一起,可以唯一地确定 f ( t ) f(t) f(t)。即:
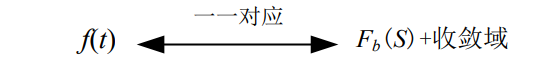
(2) 不同的信号可以有相同的 F b ( s ) F_b(s) Fb?(s),但收敛域不同。
3 (因果信号)单边拉氏变换的定义
通常遇到的信号都有初始时刻,不妨设其初始时刻为坐标原点。这样,
t
<
0
t<0
t<0时,
f
(
t
)
=
0
f(t)=0
f(t)=0。从而拉氏变换式写为
F
(
s
)
=
∫
0
?
∞
f
(
t
)
e
?
s
t
?
d
t
F(s)=\int_{0_{-}}^{\infty} f(t) \mathrm{e}^{-s t} \mathrm{~d} t
F(s)=∫0??∞?f(t)e?st?dt
称为单边拉氏变换。简称拉氏变换。其收敛域一定是 R e [ s ] > α Re[s]>\alpha Re[s]>α,可以省略。
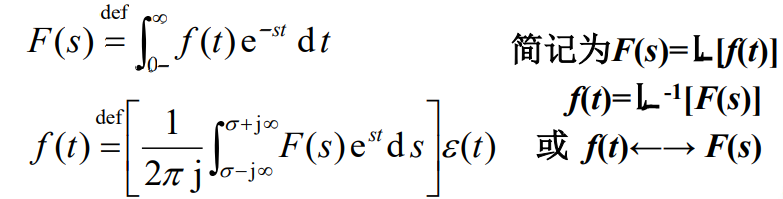
ε ( t ) \varepsilon(t) ε(t):单边, t t t小于零部分 f ( t ) f(t) f(t)值为零。
4 单边拉氏变换与傅里叶变换的关系


备注:
∫
1
a
2
+
x
2
d
x
=
1
a
arctan
?
x
a
+
C
\int \frac{1}{a^{2}+x^{2}} d x=\frac{1}{a} \arctan \frac{x}{a}+C
∫a2+x21?dx=a1?arctanax?+C
当
w
=?
0
w\not = 0
w?=0时,
lim
?
σ
→
0
σ
σ
2
+
ω
2
=
0
=
π
δ
(
ω
)
\lim _{\sigma \rightarrow 0} \frac{\sigma}{\sigma^{2}+\omega^{2}}=0=\pi\delta(\omega)
σ→0lim?σ2+ω2σ?=0=πδ(ω)
当
w
=
0
w= 0
w=0时,极限值为无穷大,等价于冲激函数
δ
(
w
)
\delta(w)
δ(w),面积为
π
\pi
π:
∫
?
∞
∞
σ
σ
2
+
ω
2
d
ω
=
arctan
?
(
x
σ
)
∣
?
∞
+
∞
=
π
\int_{-\infty}^{\infty}\frac{\sigma}{\sigma^{2}+\omega^{2}}d\omega= \arctan (\frac{x}{\sigma})|_{-\infty}^{+\infty}=\pi
∫?∞∞?σ2+ω2σ?dω=arctan(σx?)∣?∞+∞?=π
即
π
δ
(
w
)
\pi\delta(w)
πδ(w)。

5 常见信号的拉普拉斯变换
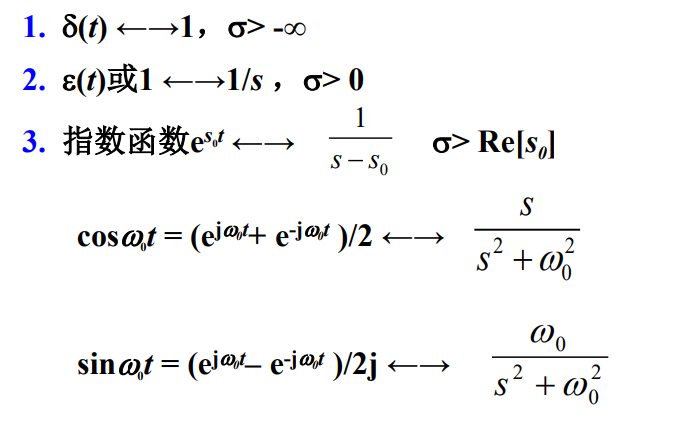

6 拉普拉斯变换的性质
6.1 线性、尺度变换


6.2 时移、复频移特性

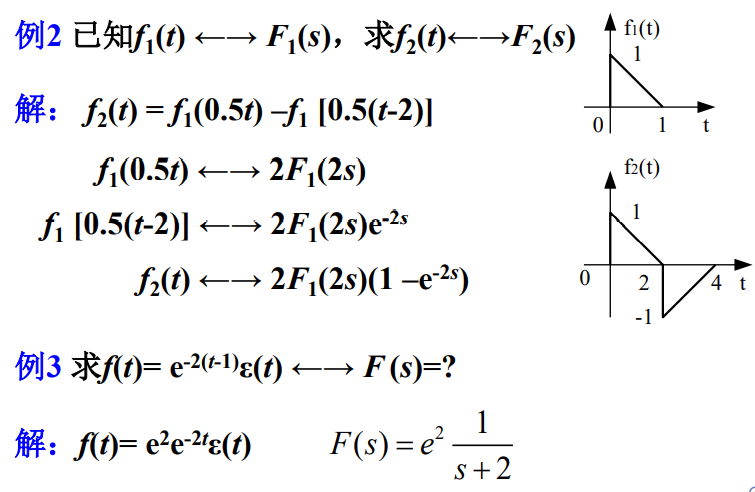

6.3 时域和复频域的微积分特性


我们可以通过求原函数倒数的拉氏变换来求原函数的拉氏变换。


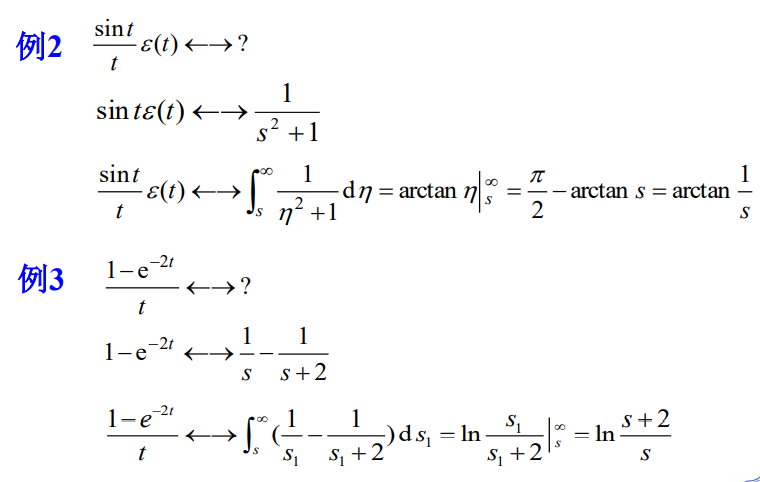
6.4 卷积定理

6.5 初值、终值定理

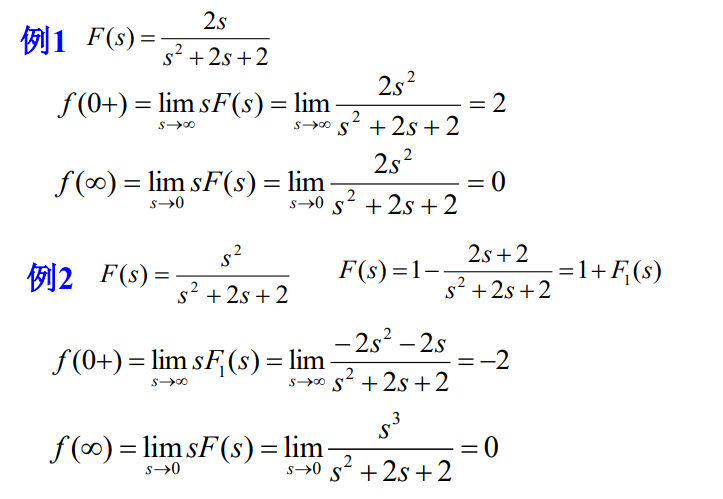
7 拉普拉斯反变换
直接利用定义式求反变换—复变函数积分,比较困难。常用的方法 :
(1)查表 ;
(2)利用性质;
(3) 部分分式展开 ----- 结合
若象函数
F
(
s
)
F(s)
F(s)是
s
s
s 的有理分式,可写为
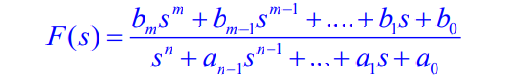
若 m ≥ n m ≥ n m≥n (假分式), 可用多项式除法将象函数 F ( s ) F(s) F(s)分解为有理多项式 P ( s ) + 有 理 真 分 式 P(s)+有理真分式 P(s)+有理真分式
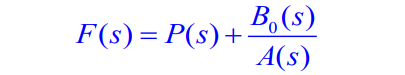
例如:
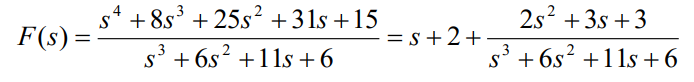
P ( s ) P(s) P(s)的拉普拉斯逆变换由冲激函数( δ \delta δ)及其各阶导数( δ ′ \delta' δ′, δ ′ ′ \delta'' δ′′…)构成。
下面主要讨论有理真分式。
部分分式展开法


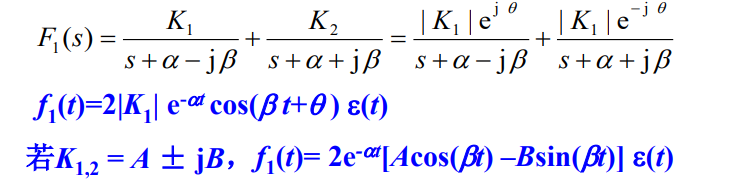
1 s ? ( ? α + j β ) → e ( ? α + j β ) t \frac{1}{s-(-\alpha+j\beta)}\rightarrow e^{(-\alpha+j\beta)t} s?(?α+jβ)1?→e(?α+jβ)t
1 s ? ( ? α ? j β ) → e ( ? α ? j β ) t \frac{1}{s-(-\alpha-j\beta)}\rightarrow e^{(-\alpha-j\beta)t} s?(?α?jβ)1?→e(?α?jβ)t
由欧拉公式,得到:
e
j
θ
?
e
(
?
α
+
j
β
)
t
+
e
?
j
θ
?
e
(
?
α
?
j
β
)
t
e^{j\theta}\cdot e^{(-\alpha+j\beta)t}+e^{-j\theta}\cdot e^{(-\alpha-j\beta)t}
ejθ?e(?α+jβ)t+e?jθ?e(?α?jβ)t
=
e
?
α
(
e
j
(
θ
+
β
t
)
+
e
?
j
(
θ
+
β
t
)
)
=e^{-\alpha}(e^{j(\theta+\beta t)}+e^{-j(\theta+\beta t)})
=e?α(ej(θ+βt)+e?j(θ+βt))
=
2
e
?
α
cos
?
(
β
t
+
θ
)
=2e^{-\alpha}\cos(\beta t+\theta)
=2e?αcos(βt+θ)
真分式:
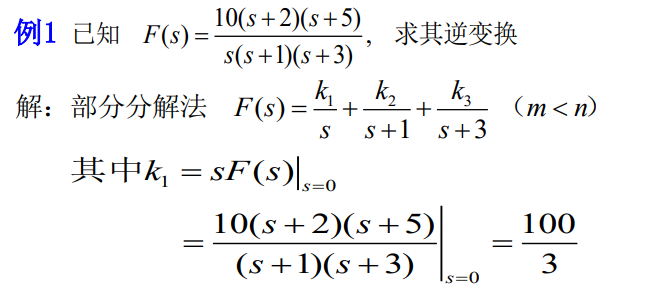
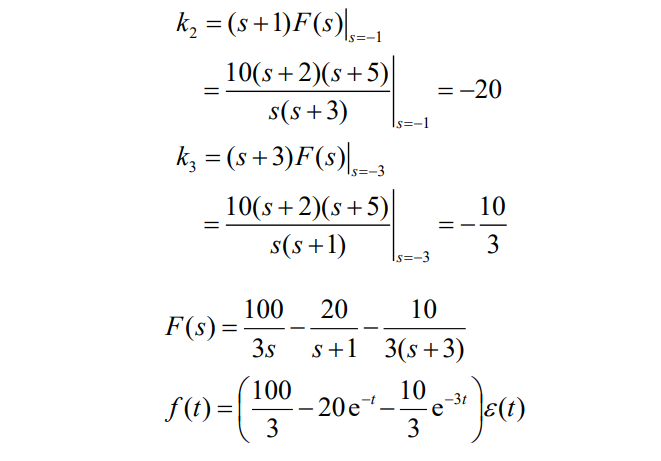
假分式:

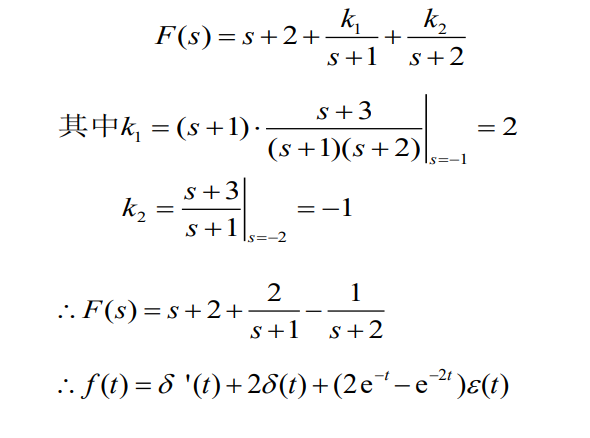
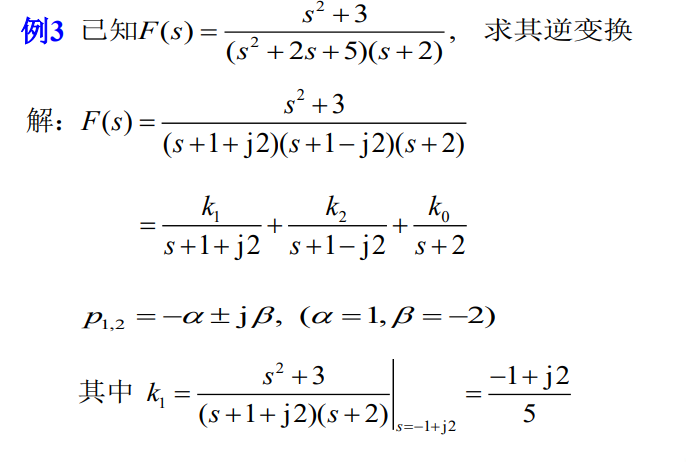
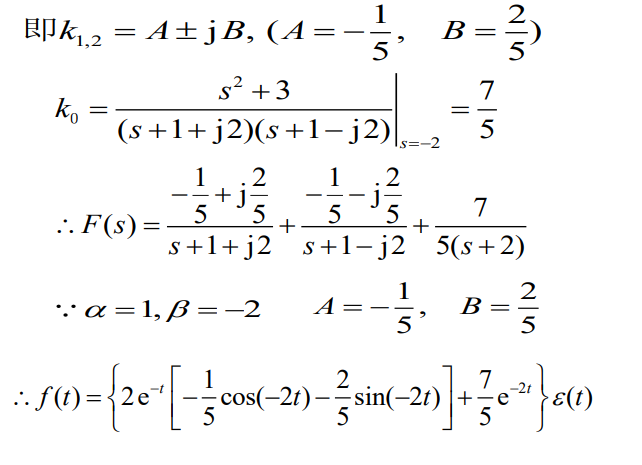


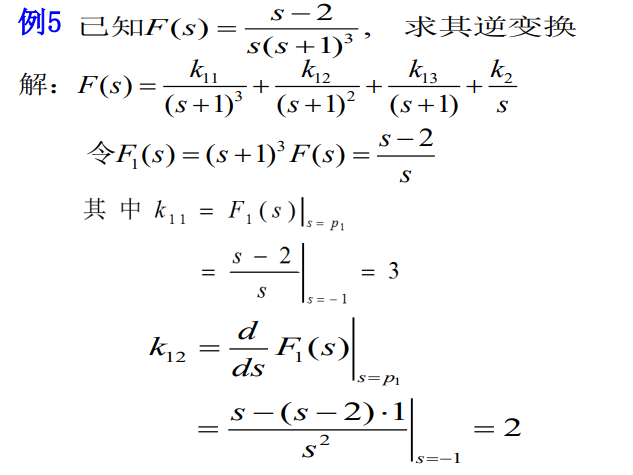
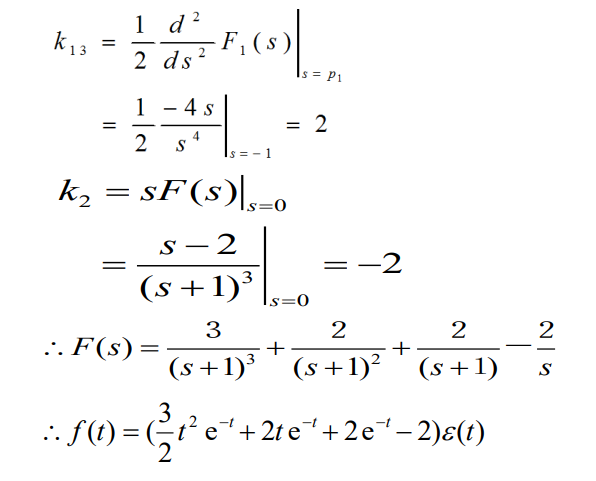
中国大学MOOC:信号与系统 ,西安电子科技大学,郭宝龙,朱娟娟