leetcode之动态规划刷题总结6
动态规划(英语:Dynamic programming,简称 DP)是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
动态规划常常适用于有重叠子问题和最优子结构性质的问题,并且记录所有子问题的结果,因此动态规划方法所耗时间往往远少于朴素解法。
动态规划有自底向上和自顶向下两种解决问题的方式。自顶向下即记忆化递归,自底向上就是递推。
使用动态规划解决的问题有个明显的特点,一旦一个子问题的求解得到结果,以后的计算过程就不会修改它,这样的特点叫做无后效性,求解问题的过程形成了一张有向无环图。动态规划只解决每个子问题一次,具有天然剪枝的功能,从而减少计算量。
1-戳气球
题目链接:题目链接戳这里!!!
思路:动态规划
用dp[i][j]表示填满区间(i,j)能得到的最多硬币,用val数组改造原来的数组nums,在原数组的首尾各添加一个1,如果是戳气球,可能使得气球的相对位置发生改变,故我们倒过来看,从后往前添加气球,状态转移方程如下:
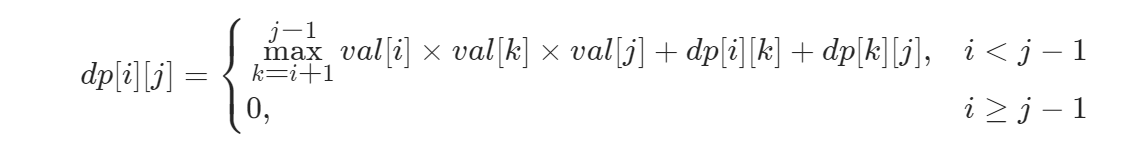
class Solution {
public int maxCoins(int[] nums) {
int n = nums.length ;
int [] val = new int [n+2] ;
int [][] dp = new int [n+2][n+2] ; //填完区间所能得到的最多硬币
val[0] = val[n+1] = 1 ;
for(int i=1; i<=n; i++){ //将原数组改造成两端各有一个1的数组
val[i] = nums[i-1] ;
}
for(int i=n-1; i>=0; i--){ //从后向前遍历,防止相邻元素被改动
for(int j=i+2; j<n+2; j++){
for(int k=i+1; k<j; k++){
int sum = val[i] * val[k] * val[j] ;
sum += dp[i][k] + dp[k][j] ;
dp[i][j] = Math.max(sum, dp[i][j]) ;
}
}
}
return dp[0][n+1] ;
}
}
思路2:记忆化搜索
自顶向下的记忆化搜索,每次枚举填充的中间位置,然后记忆化搜索即可。
我们定义方法 dfs,令 dfs(i,j) 表示将开区间(i,j) 内的位置全部填满气球能够得到的最多硬币数。由于是开区间,因此区间两端的气球的编号就是 i 和 j,对应着 val[i] 和 val[j]。
class Solution {
int [] val ;
int [][] ans ;
public int maxCoins(int[] nums) {
//自顶向下,记忆化搜索
int n = nums.length ;
val = new int [n+2] ;
ans = new int [n+2][n+2] ;
val[0] = val[n+1] = 1 ;
for(int i=1; i<=n; i++){
val[i] = nums[i-1] ;
}
for(int i=0; i<ans.length; i++){
Arrays.fill(ans[i], -1) ;
}
return dfs(0,n+1) ;
}
public int dfs(int left, int right){
if(left>=right-1){ //出口
return 0 ;
}
if(ans[left][right]!=-1){ //记忆化
return ans[left][right] ;
}
for(int i=left+1; i<right; i++){
int sum = val[left] * val[i] * val[right] ;
sum += dfs(left,i) + dfs(i,right) ;
ans[left][right] = Math.max(ans[left][right], sum) ;
}
return ans[left][right] ;
}
}
2-交错字符串
题目链接:题目链接戳这里!!!
思路:动态规划
f(i,j)表示s1的前i个元素和s2的前j个元素能否交错组成s3的i+j个元素,我们可以发现
如果 s1 的第 i 个元素和 s3 的第 i+j 个元素相等,那么 s1的前 i 个元素和 s2 的前 j 个元素是否能交错组成 s3的前 i+j 个元素取决于 s1的前 i?1 个元素和 s2 的前 j 个元素是否能交错组成 s3 的前i+j?1 个元素,即此时f(i,j) 取决于f(i?1,j),在此情况下如果 f(i?1,j) 为真,则 f(i,j) 也为真,同理,如果 s2的第 j个元素和 s3的第 i+j 个元素相等并且f(i,j?1) 为真,则f(i,j) 也为真。
class Solution {
public boolean isInterleave(String s1, String s2, String s3) {
//f[i][j]表示s1的前i个元素和s2的前j个元素能否交错组成s3的前i+j个元素
int n = s1.length(), m = s2.length(), t = s3.length() ;
if(m+n != t){
return false ;
}
boolean [][] f = new boolean[n+1][m+1] ;
f[0][0] = true ;
for(int i=0; i<=n; i++){
for(int j=0; j<=m; j++){
if(i>0){
f[i][j] = f[i][j] || (f[i-1][j] && s1.charAt(i-1) == s3.charAt(i+j-1)) ;
}
if(j>0){
f[i][j] = f[i][j] || (f[i][j-1] && s2.charAt(j-1) == s3.charAt(i+j-1)) ;
}
}
}
return f[n][m] ;
}
}
3-乘积最大子数组
题目链接:题目链接戳这里!!!
思路:动态规划
需要维护两个数组,一个数组maxF[i]表示以i结尾的最大子数组的乘积,minF[i]表示以i结尾的最小子数组的乘积。
class Solution {
public int maxProduct(int[] nums) {
//maxF[i]表示以i结尾的最大子数组的乘积,minF[i]表示以i结尾的最小子数组的乘积
int n = nums.length ;
int [] maxF = new int [n] ;
int [] minF = new int [n] ;
for(int i=0; i<n; i++){
maxF[i] = nums[i] ;
minF[i] = nums[i] ;
}
for(int i=1; i<n; i++){
maxF[i] = Math.max(maxF[i-1]*nums[i], Math.max(nums[i], minF[i-1]*nums[i])) ;
minF[i] = Math.min(minF[i-1]*nums[i], Math.min(nums[i], maxF[i-1]*nums[i])) ;
}
int ans = maxF[0] ;
for(int i=1; i<n; i++){
ans = Math.max(ans, maxF[i]) ;
}
return ans ;
}
}
4-最大平均值和分组
题目链接:题目链接戳这里!!!
思路:记忆化搜索
通过记忆化搜索枚举每一种分割情况来得到最终的最大值。使用memo[index][k]:用于记忆以index为起始分割点分割k个子集的最大平均值。
class Solution {
double [][] memo ;
public double largestSumOfAverages(int[] nums, int k) {
this.memo = new double[nums.length+1][k+1] ;
return dfs(nums,k,0) ;
}
public double dfs(int [] nums, int k, int index){
if(k==0){
return 0.0 ;
}
if(memo[index][k] != 0.0){
return memo[index][k] ;
}
if(k==1){
double sum = 0 ;
for(int i=index; i<nums.length; i++){
sum += nums[i] ;
}
memo[index][k] = sum / (nums.length-index) ;
return memo[index][k] ;
}
double ans = 0.0, sum = 0.0 ;
for(int i=index; i<=nums.length-k; i++){
sum += nums[i] ;
double avg = sum / (i - index + 1) ;
memo[i+1][k-1] = dfs(nums,k-1,i+1) ;
ans = Math.max(ans, avg+memo[i+1][k-1]) ;
}
memo[index][k] = ans ;
return ans ;
}
}
5-数组中的最长山脉
题目链接:题目链接戳这里!!!
思路:中心扩张法,每次找到一个比左右两侧都大的数,然后依次向两侧扩张。
class Solution {
public int longestMountain(int[] arr) {
//中心扩张法
if(arr.length<3){
return 0 ;
}
int ans = 0 ;
for(int i=1; i<arr.length-1; i++){
if(arr[i]>arr[i-1] && arr[i]>arr[i+1]){
int l = i - 1 ;
int r = i + 1 ;
while(l>0 && arr[l-1]<arr[l]){
l -- ;
}
while(r<arr.length-1 && arr[r+1]<arr[r]){
r ++ ;
}
ans = Math.max(ans, r-l+1) ;
}
}
return ans ;
}
}
6-最长等差数列
题目链接:题目链接戳这里!!!
思路:动态规划
dp[i][d]:表示当前下标为i时的等差为d的等差数列个数。
class Solution {
public int longestArithSeqLength(int[] nums) {
int [][] dp = new int [1001][1001] ;
int ans = 0 ;
for(int i=0; i<nums.length; i++){
for(int j=0; j<i; j++){
int d = nums[i] - nums[j] + 500 ;
dp[i][d] = Math.max(dp[i][d], dp[j][d]+1) ;
ans = Math.max(ans,dp[i][d]) ;
}
}
return ans + 1 ;
}
}
7-将字符串翻转到单调递增
题目链接:题目链接戳这里!!!
思路1:指针模拟法,从头开始,依次记录0的个数和1的个数,当0的个数大于1的个数则翻转1,同时重新从该位置开始记录0和1的个数,最后结束后翻转0.
class Solution {
public int minFlipsMonoIncr(String s) {
int n = s.length() ;
int p = 0 ;
int zero = 0 , one = 0, ans = 0 ;
while(p<n){
if(s.charAt(p) == '0'){
zero ++ ;
}else if(s.charAt(p)=='1'){
one ++ ;
}
if(zero>one){
ans += one ;
zero = one = 0 ;
}
p ++ ;
}
ans += zero ;
return ans ;
}
}
思路2:动态规划
定义dp[i][0], dp[i][0]表示前i个元素递增且第i个元素为0的最小翻转次数,
定义dp[i][1], dp[i][1]表示前i个元素递增且第i个元素为1的最小翻转次数。
由定义可知,如果前i个元素最后以0结尾且满足单调递增,那么前i个元素必须全部为0,由此可得 dp[i][0] 的状态转移如下:
dp[i][0] = dp[i-1][0] + (s.charAt(i)‘0’ ? 0 : 1);
由定义可知, dp[i][1]只要满足最后一个元素为1就行,那么前i-1个元素既可以为0,也可以为1,因此dp[i][1]的状态转移如下:
dp[i][1] = min(dp[i-1][1] , dp[i-1][0]) + (s.charAt(i) ‘1’ ? 0: 1);
最后取dp[i][0],dp[i][1]中的较小的即可。
class Solution {
public int minFlipsMonoIncr(String s) {
//dp[i][0]表示前i个元素以0结尾的最小翻转使得单调递增次数
//dp[i][1]表示前i个元素以1结尾的最小翻转使得单调递增函数
int n = s.length() ;
int [][] dp = new int [n][2] ;
dp[0][0] = (s.charAt(0)=='0' ? 0 : 1) ;
dp[0][1] = (s.charAt(0)=='1' ? 0 : 1) ;
for(int i=1; i<n; i++){
dp[i][0] = dp[i-1][0] + (s.charAt(i) =='0' ? 0 : 1) ;
dp[i][1] = Math.min(dp[i-1][0],dp[i-1][1]) + (s.charAt(i)=='1' ? 0 : 1) ;
}
return Math.min(dp[n-1][0],dp[n-1][1]) ;
}
}
8-分隔数组以得到最大和
题目链接:题目链接戳这里!!!
思路:dp[i]表示前i个字符串分割为长度最多为k的连续子数组得到的最大和,我们可以发现如果元素的个数小于等于k,则找出元素的最大值乘以元素个数即可,如果k的值小于元素个数,则递推表达式 dp[i] = Math.max(dp[i],dp[i-j]+max(arr, i-j+1, i)*j) ;
class Solution {
public int maxSumAfterPartitioning(int[] arr, int k) {
int n = arr.length ;
int [] dp = new int [n] ;
for(int i=1; i<=k; i++){
dp[i-1] = max(arr, 0, i-1) * i ;
}
for(int i=k; i<n; i++){
for(int j=1; j<=k; j++){
dp[i] = Math.max(dp[i],dp[i-j]+max(arr, i-j+1, i)*j) ;
}
}
return dp[n-1] ;
}
public int max(int [] arr, int start, int end){
int max = arr[start] ;
for(int i=start+1; i<=end; i++){
max = Math.max(max, arr[i]) ;
}
return max ;
}
}
**
道阻且长,行则将至,一步一个脚印,加油吧!!!
**