Task08:搜索
1. 视频题目
1.1 二分查找
1.1.1 描述
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
提示:
你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999, 9999]之间。
1.1.2 代码
左右两个下标,分别在不同的情况下左移或者右移
class Solution:
def search(self, nums: List[int], target: int) -> int:
low = 0
high = len(nums)-1
while low<=high:
mid = low+(high-low)//2
# 取中点
if nums[mid] == target:
return mid
# 找到即返回
elif nums[mid] < target:
low = mid+1
# 中点偏小则右移
else:
high = mid-1
# 中点偏大则右移
return -1
1.1.3 总结
中止条件是左右指针错开,相等时仍旧符合条件
而且求中点最好用low+(high-low)//2,防止溢出
1.2 搜索旋转排序数组
1.2.1 描述
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
示例 1:
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
示例 2:
输入:nums = [4,5,6,7,0,1,2], target = 3
输出:-1
示例 3:
输入:nums = [1], target = 0
输出:-1
提示:
1 <= nums.length <= 5000
-10^4 <= nums[i] <= 10^4
nums 中的每个值都 独一无二
题目数据保证 nums 在预先未知的某个下标上进行了旋转
-10^4 <= target <= 10^4
进阶:你可以设计一个时间复杂度为 O(log n) 的解决方案吗?
1.2.2 代码
其实如果直接暴力的话,是不是可以先把数组变有序,然后再找
就是直接找到开始旋转的点,然后重新拼接,然后再二分查找
说回不改变数组,也就是在原数组上查找,无非是多判断一些情况
大框架上与之前的二分一致,都是取中点比较与目标的大小,然后调整区间
这里需要注意的是,调整区间的时候,要主要此时左右哪个区间有序
也就是,比较完大小之后,下一步是判断有序区间,然后才是调整区间
class Solution:
def search(self, nums: List[int], target: int) -> int:
low = 0
high = len(nums)-1
while low<=high:
# 当两点存在区间,允许相等
mid = low + (high-low)//2
# 取中点
if nums[mid]==target :
return mid
# 相等则返回
elif target<nums[mid] :
# 如果目标值更小
if nums[low]<=nums[mid]:
# 如果是左有序的,允许相等
if nums[low]==target:
return low
# target比中点小
# 左有序,左比中点小
# 因此比较左端点和target
# 相等则返回
elif nums[low]<target:
# target比左端点大
# target比中点小
# 因此在左区间内
high = mid-1
else :
# 否则就是
# target比左端点小
# target比中点小
# 因此在右区间内
low = mid+1
else:
# 否则就是右有序的
# target比中点小
# 中点比右端点小
# 因此在左区间内
high = mid-1
else :
# 如果目标值更大
if nums[mid]<=nums[high]:
# 如果是右有序的,允许相等
if nums[high]==target:
return high
# target比中点大
# 右有序,右比中点大
# 因此比较右端点和target
# 相等则返回
elif target < nums[high]:
low = mid+1
# target比中点大
# target比右端点小
# 右有序
# 因此在右区间内
else :
high = mid-1
# target比中点大
# target比右端点大
# 右有序
# 因此在左区间内
else :
# 否则就是左有序的
low = mid+1
# target比中点大
# target比左区间大
return -1
还有一个精简的写法:
class Solution:
def search(self, nums: List[int], target: int) -> int:
if not nums:
return -1
# 数组为空
l, r = 0, len(nums) - 1
# 左右边界
while l <= r:
mid = (l + r) // 2
# 中点
if nums[mid] == target:
return mid
# 相等则返回
if nums[0] <= nums[mid]:
# 左有序情况
if nums[0] <= target < nums[mid]:
r = mid - 1
# 在有序区间内
else:
# 不再有序区间内
l = mid + 1
else:
# 右有序情况
if nums[mid] < target <= nums[len(nums) - 1]:
l = mid + 1
# 在有序区间内
else:
r = mid - 1
# 不再有序区间内
return -1
1.2.3 总结
我之前的代码,在判断有序的时候,忘记加等号了,所以就报错了
也就是说,假如左区间像是[2,2,2,2,2,2],这是有序的,也就是符合nums[left]<=nums[mid]
我刚开始没发现问题,我还以为是步骤顺序的问题,因为我是先比较中值,再判断有序区间
而视频和题解的方案一般都是,先判断区间,再比较中值,后来发现不是这个的问题
所以在比较大小的时候,一定要注意相等的这个临界条件,不能随便地归给else
2. 作业题目
2.1 对称二叉树
2.1.1 描述
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
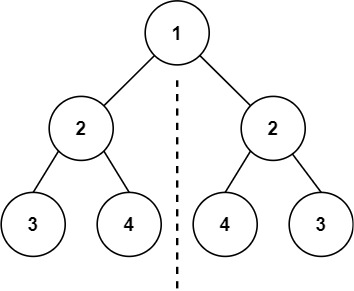
输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:
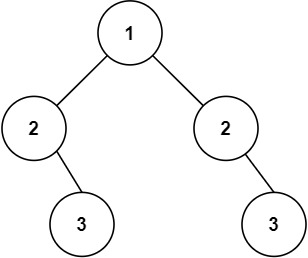
输入:root = [1,2,2,null,3,null,3]
输出:false
提示:
树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100
进阶:你可以运用递归和迭代两种方法解决这个问题吗?
2.1.2 代码
我最开始的思路,直接就是层次遍历,广度优先搜索,然后就出问题了

像是示例二这种的,如果遍历到第三层,层内元素的值,正序等于逆序,程序认为合格
但是实际上来说,这两个数值相等的节点,一个在左一个在右,事实上是不对称的
对于这个bad case,我想到的解决办法是补充上另一边缺失的节点,但是需要另一边有值
也就是,如果左孩子缺失,此时检查右孩子,如果存在右孩子,那就补充左孩子
当时这么做,主要是考虑到要避免死循环,否则一直补充下去,无穷无尽,但是还不行
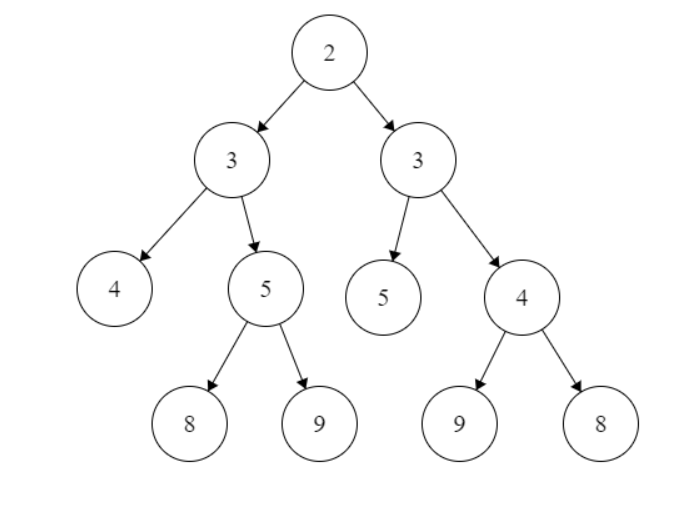
有这么一个bad case,由于左边的4和右边的5都没有孩子,所以说程序是不会给他们补充子女的
这也就导致了当遍历到叶子节点的这一层,程序会判断对称,但实际上叶子节点的父节点并不对称
所以问题可能还是出在对空节点数值的补充上,我想到之所以遍历不到空节点,是因为并没有将其入队
一般的广度优先搜索,会事先判断孩子是否为空,然后再将孩子入队,所以说就跳过了空节点的遍历
那遍历到空节点似乎也没什么问题吧,改为不检查是否为空,直接将非空节点左右孩子都给入队了
所以说遍历到空节点的时候,我们不访问起.val,而是随便加一个范围外的值,标识这个空节点
然后,就给,过了!过了!过了!我当时其实还是有点担忧下,例如下面这种情况
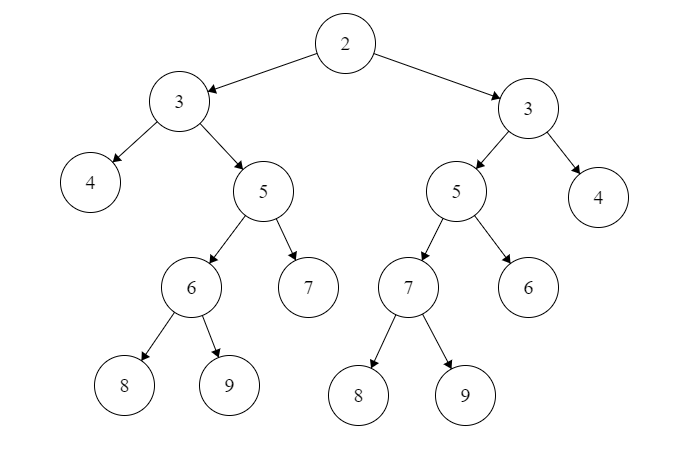
我原本是在想,如果在上面的基础上,再加一层,就像6和7这一层下面才是8和9这一层,会不会出问题
然后发现并不会,遍历到6和7的时候直接给过了,并且不影响8和9的null,也不影响判断8和9的对称
所以说,当叶子节点在8和9这一层的时候,影响其对称的空节点,只跟6和7有关,与4和5无关
4和5对判断对称的影响,只到下一层,即6和7。一旦对称之后,再往下到8和9就无关了,补齐也是对称的
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if not root:
return True
# 为空则直接返回
queue = []
queue.append(root)
while queue :
val = []
size = len(queue)
for _ in range(size):
cur = queue.pop(0)
if cur:
val.append(cur.val)
queue.append(cur.left)
queue.append(cur.right)
else :
val.append(-200)
if val != val[::-1]:
return False
return True
这是题解思路的代码,也是层次遍历,不过是交错将孩子入队,然后两两比较
class Solution(object):
def isSymmetric(self, root):
"""
:type root: TreeNode
:rtype: bool
"""
if not root or not (root.left or root.right):
return True
# 用队列保存节点
queue = [root.left,root.right]
while queue:
# 从队列中取出两个节点,再比较这两个节点
left = queue.pop(0)
right = queue.pop(0)
# 如果两个节点都为空就继续循环,两者有一个为空就返回false
if not (left or right):
continue
if not (left and right):
return False
if left.val!=right.val:
return False
# 将左节点的左孩子, 右节点的右孩子放入队列
queue.append(left.left)
queue.append(right.right)
# 将左节点的右孩子,右节点的左孩子放入队列
queue.append(left.right)
queue.append(right.left)
return True
2.1.3 总结
深度和广度优先的适用方向还是不同的,本题从广度的方向思考起来就比较直观
然后就是做题的时候一定要仔细思考题中给出的测试用例,寻找规律,再考虑特殊情况
这里其实是有点像,比较当前子树的叶子节点层的对称,所以说即便是空节点也要入队遍历
只不过是遍历访问到空节点的时候,将标记空节点的值放入列表,而不是节点的数值
2.2 二叉树的中序遍历
2.2.1 描述
给定一个二叉树的根节点 root ,返回它的 中序 遍历。
示例 1:
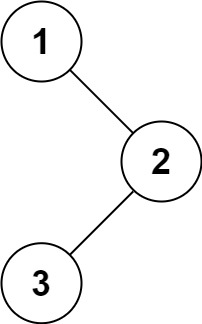
输入:root = [1,null,2,3]
输出:[1,3,2]
示例 2:
输入:root = []
输出:[]
示例 3:
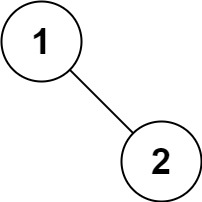
输入:root = [1]
输出:[1]
示例 4:
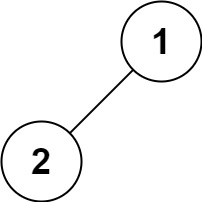
输入:root = [1,2]
输出:[2,1]
示例 5:
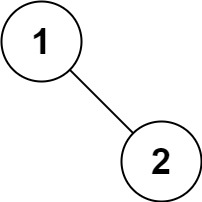
输入:root = [1,null,2]
输出:[1,2]
提示:
树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
2.2.2 代码
递归就很简单了,按照顺序访问就好。不为空了继续访问,为空就返回。
class Solution:
def inorder(self,node):
if not node:
return
self.inorder(node.left)
self.res.append(node.val)
self.inorder(node.right)
def inorderTraversal(self, root: TreeNode) -> List[int]:
self.res = []
self.inorder(root)
return self.res
迭代的话,需要显式地维护一个栈,这其实有点像Task05:树的视频里面提到的,访问次数的问题
WHITE是没有到达过,GRAY是第一次到达,第二次到达就将节点的数值加入列表
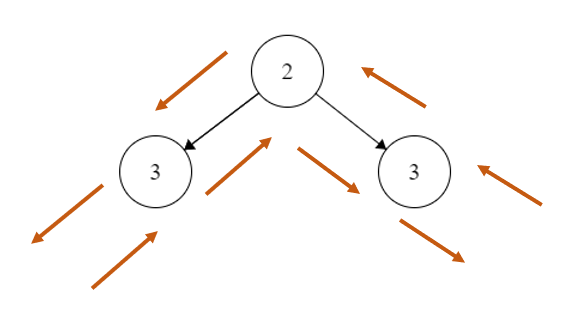
如果第一次到达一个节点就访问,那是前序,第二次是中序,第三次是后序
访问顺序照常,但是压栈的顺序要逆反过来,因为栈是先进后出
class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
WHITE, GRAY = 0, 1
res = []
stack = [(WHITE, root)]
while stack:
color, node = stack.pop()
if node is None: continue
if color == WHITE:
stack.append((WHITE, node.right))
stack.append((GRAY, node))
stack.append((WHITE, node.left))
else:
res.append(node.val)
return res
2.2.3 总结
如果第一次到达一个节点就访问,那是前序,第二次是中序,第三次是后序
2.3 二叉搜索树中第K小的元素
2.3.1 描述
给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 个最小元素(从 1 开始计数)。
示例 1:
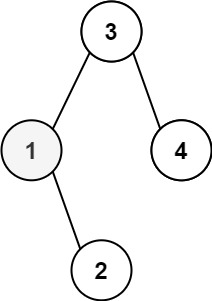
输入:root = [3,1,4,null,2], k = 1
输出:1
示例 2:
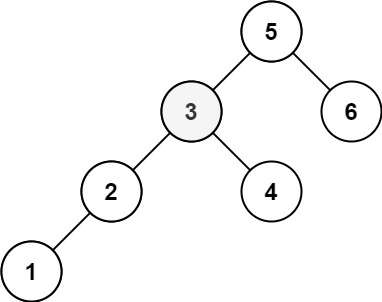
输入:root = [5,3,6,2,4,null,null,1], k = 3
输出:3
提示:
树中的节点数为 n 。
1 <= k <= n <= 104
0 <= Node.val <= 104
进阶:如果二叉搜索树经常被修改(插入/删除操作)并且你需要频繁地查找第 k 小的值,你将如何优化算法?
2.3.2 代码
二叉搜索树是一个有序的结构,其有序的访问应该是中序遍历,每遍历到一个点,计数-1即可
题解当中给的这个中序遍历还挺绕的,应该是迭代的写法,还是到达次数的那个思路
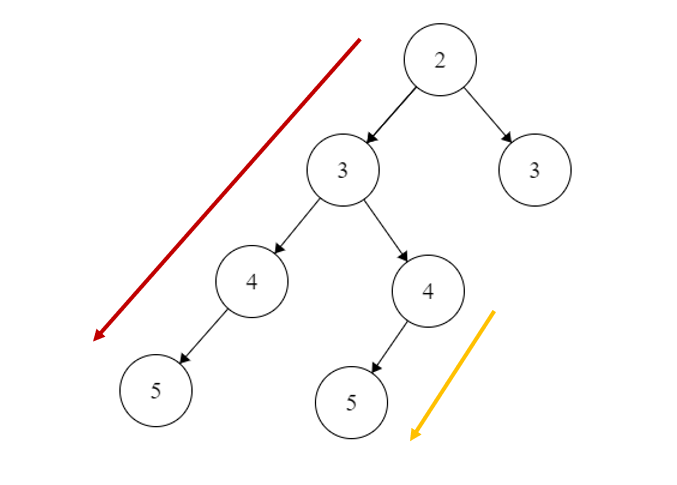
while循环第一次压入的是红色的那一列,包含了左孩子和父节点
于是栈顶每弹出一个元素访问后,就转向其右孩子
所以当红色序列访问到节点3后,while循环压入了黄色的序列
感觉不如递归的方式更加直观简洁
class Solution:
def kthSmallest(self, root: TreeNode, k: int) -> int:
stack = []
while root or stack:
while root:
stack.append(root)
root = root.left
# 一值循环到最左的节点
root = stack.pop()
# 弹出当前节点
k -= 1
# 计数-1
if k == 0:
return root.val
# 计数为0就返回
root = root.right
# 访问右子树
2.3.3 总结
二叉搜索树是一个有序的结构,其有序的访问应该是中序遍历
题中的进阶,我原本的思路是另外维护一个最小栈,但发现不行
因为这里是第k小,并不固定,可能前进也可能后退,极富变化
看题解是维护一个平衡搜索二叉树,其中的旋转步骤略难,还没看