说明一下:这里我参考的是:鲁伟的《机器学习-公式推导与代码实现》,因为《机器学习》对于公式的推导一带而过,需借助其他书籍来将公式内容推导出来,还有就是鲁伟的书有一部分内容介绍不清楚,我会将自己梳理一遍的内容写出来。应该是比较清楚的,吧。
一、普通线性回归
我们有一个数据集: D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) , . . . , ( x m , y m ) } D=\left\{ \left( x_1,y_1 \right) ,\left( x_2,y_2 \right) ,\left( x_3,y_3 \right) ,...,\left( x_m,y_m \right) \right\} D={(x1?,y1?),(x2?,y2?),(x3?,y3?),...,(xm?,ym?)}
表示 x ? y x-y x?y 平面内有 m m m 个点,即:
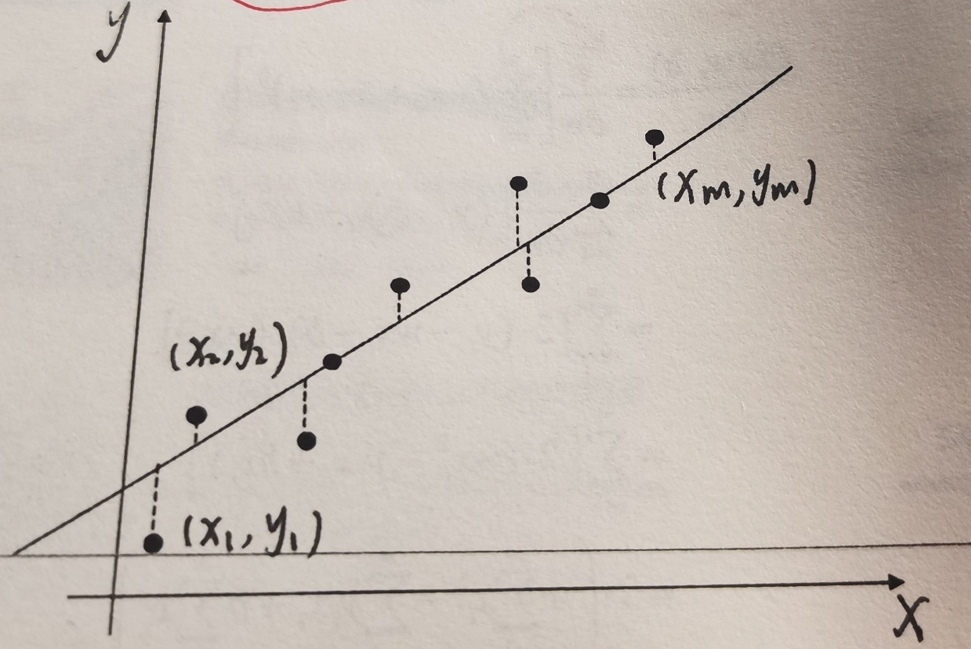
可设线性回归模型为:
y
^
=
w
x
i
+
b
\hat{y}=wx_i+b
y^?=wxi?+b
下面我们用最小二乘法来求出 w w w 和 b b b 的最优解。
最小二乘法: 令均方误差最小时,求解线性回归模型参数 w w w 和 b b b 最优值的方法。
均方误差: 每一个点的 y y y 值与预测值 y ^ \hat{y} y^? 之间的距离的平方的累加和。

该式子表明:当可以让均方误差取最小值时,所求得的参数值,就是线性回归参数
w
w
w 和
b
b
b 的最优值。
接下来,基于上面的式子分别对
w
w
w 和
b
b
b 求一阶导数并令其为0
为什么这样做,书上没有讲,个人认为是因为关于 w w w 和 b b b 的函数都为二次函数,开口向上,所以一阶导数为 0 的位置就是均方误差取得最小值的地方


二、多元线性回归
与普通线性回归有一些些区别的是,多元线性回归的模型为:
y
^
=
w
1
x
1
+
w
2
x
2
+
.
.
.
+
w
d
x
d
+
b
\hat{y}=w_1x_1+w_2x_2+...+w_dx_d+b
y^?=w1?x1?+w2?x2?+...+wd?xd?+b
上面的模型说明:预测值由 d d d 个因素(有 d d d 个自变量 x x x )影响。假设数据集一共有 m m m 个样本,则:

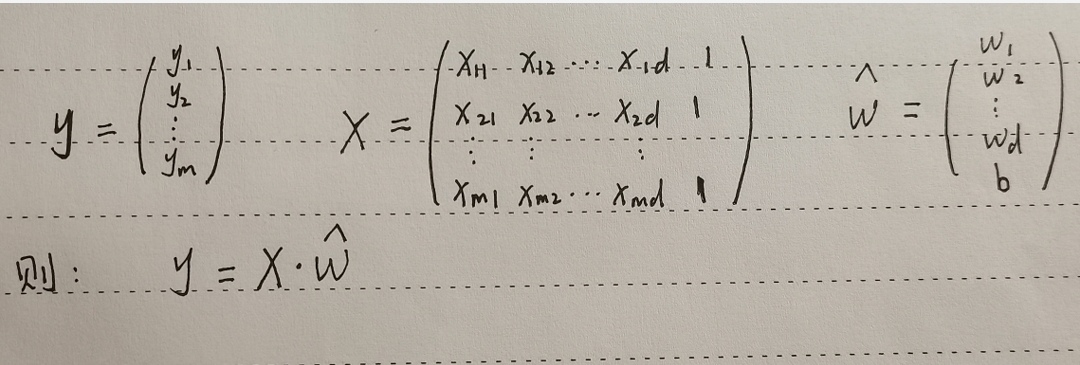

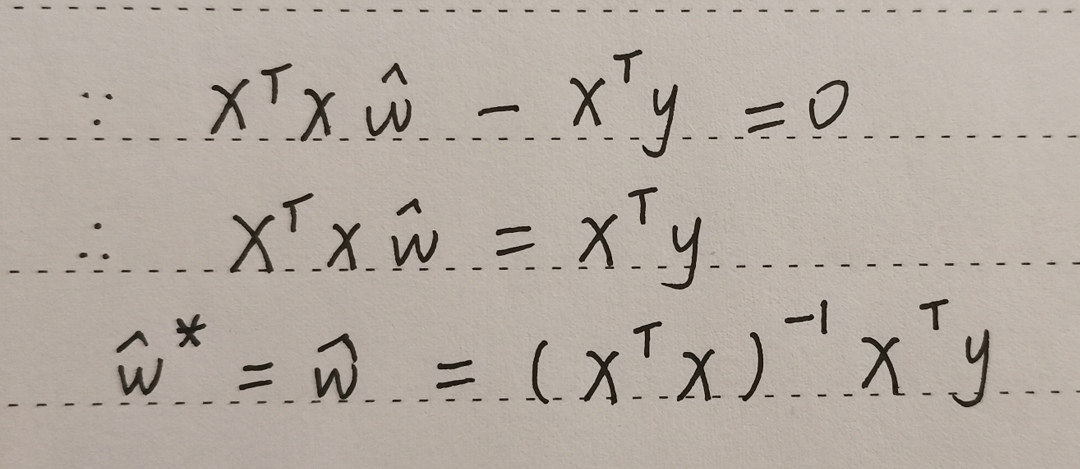
三、总结
无论是普通线性回归,还是多元线性回归,都是用了最小二乘法的方法,通过让均方误差最小化(即求导并令倒数等于0)来解方程求出参数的最优值。
对于普通线性回归模型来说,要求出两个参数的最优值;而对于多元线性回归模型来说,其将 w w w 和 b b b 合成一个矩阵,再运用矩阵的相关知识求出该矩阵的最优值。
当我们有了相关模型的参数的表达式时,我们就可以通过数据来训练出我们想要的线性回归模型了,接下来就是通过编程实现其过程。
还有要说的是,这并不是线性回归公式推导的全部内容,还有将上述参数的表达式进行正则化的过程没有列出来,正则化过程主要用于防止过拟合。