文章目录
D.前缀和
基础知识
1.用途:
可以快速地求出一个静态数组(不会被修改)中某一个区间内所有数的和,有效提高运行效率
2.暴力:
时间复杂度为O(N)
//[l,r] 时间复杂度:O(N)
for(int i=l;i<=r;i++) res+=a[i];
3.思想:
定义原数组a[ ]和前缀和数组s[ ]
//a[]为原数组,s[]为前缀和数组
s[0]=0 //特殊规定
s[i]=a[1]+a[2]+...+a[i] //s[i]表示原数组的前i个数的和
...
s[n]=a[1]+a[2]+...+a[n]
第一步:预处理前缀和数组,时间复杂度O(N)
//预处理s数组,O(N)的时间复杂度很快
for(int i=1;i<=n;i++) s[i]=s[i-1]+a[i];
第二步:查询,时间复杂度O(1)
//查询 [l,r] ,O(1)的时间复杂度
a[l]+a[l+1]+a[l+2]+...+a[r]=s[r]-s[l-1]
//当预处理完s数组之后,再去算某一段区间的时候,就肯容易了
//直接算s数组两个端点的差值就可以了,只算一次即可,将暴力查询时的O(N)时间复杂度降到O(1)
4.注意:
前缀和:只能修改静态数组即只能查询不能修改
树状数组和线段树:可以操作动态数组,可以边查询边修改,但查询和修改的时间都是O(logN)的
5.总结:
/*
若输入量为N,进行M次查询,则:
a.暴力:执行求前缀和单次查询的操作是O(N)的,但是若有m次查询,暴力是那就是O(M*N)
b.前缀和;需要预处理为O(N),单词查询的时间复杂度为O(1),若有m次查询,那就是O(M)
前缀和相当于是把暴力算法拆解开来了
将时间复杂度从O(N)降到O(1),但只能查询,不能修改,即只能对静态数组进行操作
c.树状数组和线段树:既能查询,又能修改,是对动态数组进行操作,但查询和修改时间复杂度都是O(logN)
*/
例题
一、前缀和
1.基本思路:
同上
2.代码模板:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;//数据范围
int n, m;
int a[N]; // 表示原数组
int s[N]; // 表示前缀和数组
//以上两个数组其实还可以混到一起,为了好理解分开
//边界:只要前缀和是从1开始的,并且前缀和数组中s[0]=0的话,边界就没有问题。否则,还要加一个特判
int main()
{
scanf("%d%d", &n, &m);//n代表数列长度,m表示询问的个数
for (int i = 1; i <= n; i ++ ) //下标从1开始
{
scanf("%d", &a[i]); //读入n个数
s[i] = s[i - 1] + a[i]; // 预处理前缀和数组
//注意s[0]在这里是不用初始化的,因为定义的是全局数组,初始值为0;如果定义为局部数组的话,初值为随机值
}
while (m -- )//处理m个询问
{
int l, r;
scanf("%d%d", &l, &r); //读入区间范围
printf("%d\n", s[r] - s[l - 1]);
}
return 0;
}
二、子矩阵的和
1.基本思路:
二维前缀和(前缀和矩阵),对一维前缀和的扩展
定义原数组a[ ][ ]和前缀和数组s[ ][ ]
//a[]为原数组,s[]为前缀和数组
//s[][]中每一个数表示原矩阵当中左上角的所有数的和
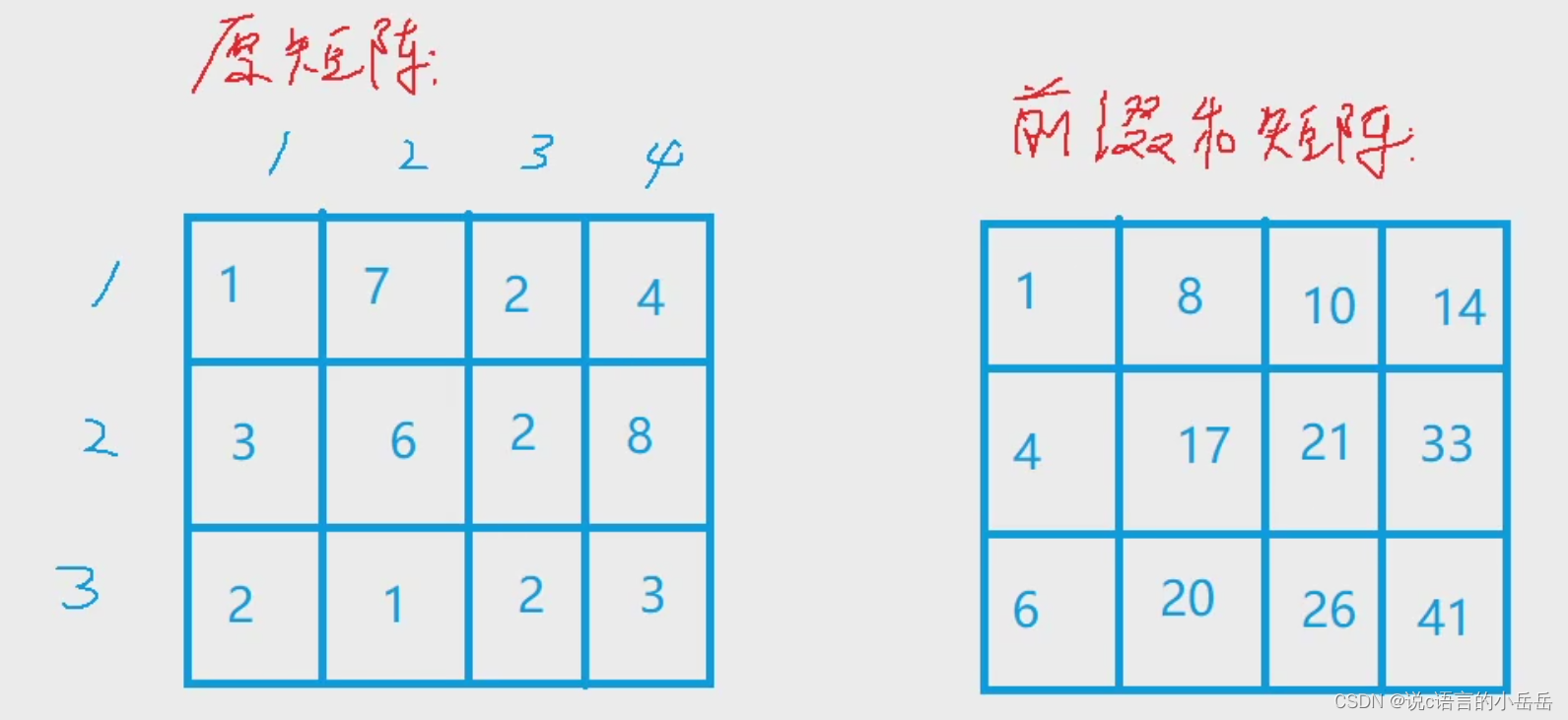
第一步:预处理二维前缀和数组,时间复杂度O(N*M)
//即思考如何计算前缀和矩阵?——容斥原理
s[x][y]=s[x-1][y]+s[x][y-1]-s[x-1][y-1]+a[x][y]
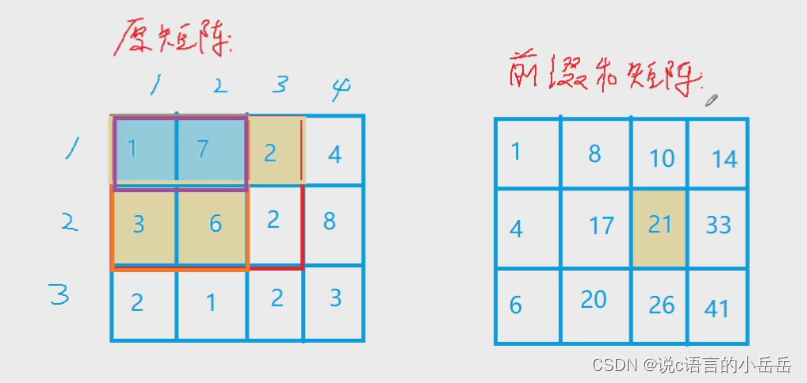
第二步:查询,时间复杂度O(1)
//即思考如何利用前缀和矩阵计算某一个子矩阵的和?——容斥原理
已知子矩阵左上角[x1,y1],右下角[x2][y2]
ans=s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]
//将时间复杂度从O(N*M)降到O(1)
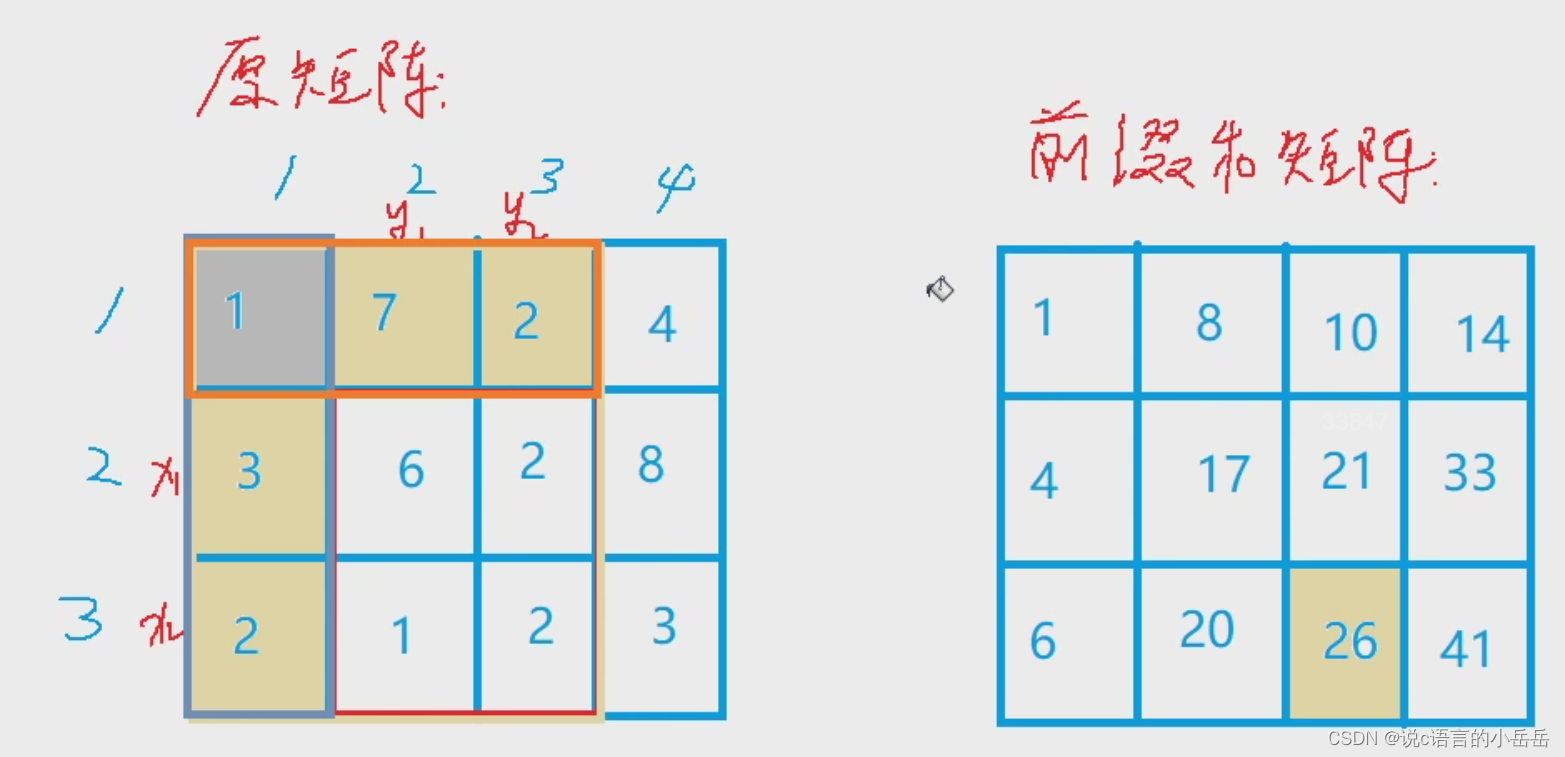
2.代码模板:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m, q;
int a[N][N], s[N][N]; //原数组和前缀和数组
int main()
{
scanf("%d%d%d", &n, &m, &q);//n,m表示原矩阵的长和宽,q表示查询的次数
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
{
scanf("%d", &a[i][j]);//读入原矩阵
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];//预处理前缀和矩阵
}
while (q -- ) //读入q次询问
{
int x1, y1, x2, y2; //x1,y1为子矩阵左上角;x2,y2为子矩阵的右下角
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]); //查询
}
return 0;
}
三、激光炸弹
1.基本思路
(1)注意:
①R最大取到5001:因为R最大为5000,网格边上的点可能炸不掉,取5001
②R*R的子矩阵里面总和最大的子矩阵是多少:(n-R+1) *(m-R+1)
(2)边界:
目标是在格点上,不是在边上,所以最多能摧毁的格点是R*R个,而由格点构成的矩形是(R-1) *(R-1)个
(3)思路:
枚举一下所有边长为R*R的子矩阵,求出每一个子矩阵中所有点价值的总和,取一下他们的最大值
(4)做法:
空间内存优化+二维数组前缀和——时间复杂度O(N*N)
2.代码实现
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 5010;//为了防止出现边界问题,习惯多开10个
int n, m; //n和m表示长宽
int s[N][N];
//空间优化:把原数组删掉,一开始把前缀和数组当作原数组,再去求前缀和即可,只用一个前缀和数组即可,两个可以合而为一
//这一开一个二维数组为5000*5000,大约为2500万个int,开两个的话5000万个int,大约需要200M内存,内存超限,超出本题目内存限制了,所以只能用一个二维数组
int main()
{
int cnt, R;
cin >> cnt >> R;
R = min(5001, R);//R只要大于5001,实际上和5001是没有区别的,因为x,y最大取到5000
n = m = R; //也可以写成n=m=5001,n和m一定要大于等于R,因为n和m是横纵坐标的最大值,如果比R小,那么枚举子矩阵的时候可能就枚举不到了
//为了让n和m至少能枚举一次
while (cnt -- )//输入cnt个目标的价值
{
int x, y, w;
cin >> x >> y >> w;
x ++, y ++ ;//规定所有位置都是大于等于1的,这样就不用处理特殊情况了
//因为用前缀和时下标要求从1开始,而这里下标是从0开始计算的,所以我们就让下标往下往右移一个
n = max(n, x), m = max(m, y);//让n表示横坐标最大值,m表示纵坐标最大值
//如果不去max,x,y点可能会落在最大区域的外边
s[x][y] += w; //读入,一开始让原数组就是前缀和数组,表示原位置所有目标的价值,因为不同目标可能处在统一位置上
}
// 预处理前缀和
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1]; //注意这里就不是+a[i][j] ,而是用s[i][j],因为为了节省空间把s和a合并了
//这里的s[i][j]是存取的格点上的值,但下面是按照矩形来算的
int res = 0;
// 枚举所有边长是R的矩形,枚举(i, j)为右下角
for (int i = R; i <= n; i ++ )
for (int j = R; j <= m; j ++ )
res = max(res, s[i][j] - s[i - R][j] - s[i][j - R] + s[i - R][j - R]);
cout << res << endl;
return 0;
}
3.总结
空间内存优化+二维数组前缀和+细节问题
/*
(1)二维数组前缀和:快速的求出每个子矩阵的总和
(2)空间内存优化:
a.将原数组和前缀和数组合并:
s[x][y] += w;
//读入,一开始让原数组就是前缀和数组,表示原位置所有目标的价值,因为不同目标可能处在统一位置上
//空间优化:把原数组删掉,一开始把前缀和数组当作原数组,再去求前缀和即可,只用一个前缀和数组即可,两个可以合而为一
//这一开一个二维数组为5000*5000,大约为2500万个int,开两个的话5000万个int,大约需要200M内存,内存超限,超出本题目内存限制了,所以只能用一个二维数组
b.考虑边界问题R最大取到5001:
R = min(5001, R);
//R只要大于5001,实际上和5001是没有区别的,因为x,y最大取到5000
(3)细节问题:
a.前缀和数组下标从1开始:
x ++, y ++ ;
//规定所有位置都是大于等于1的,这样就不用处理特殊情况了
//因为用前缀和时下标要求从1开始,而这里下标是从0开始计算的,所以我们就让下标往下往右移一个
b. 保证目标点要在区域内:
n = m = R; //也可以写成n=m=5001,n和m一定要大于等于R,因为n和m是横纵坐标的最大值,如果比R小,那么枚举子矩阵的时候可能就枚举不到了
//为了让n和m至少能枚举一次
n = max(n, x), m = max(m, y);//让n表示横坐标最大值,m表示纵坐标最大值
//如果不去max,x,y点可能会落在最大区域的外边
c.不同目标可能在统一位置上:
s[x][y] += w;
//所以不是s[x][y]=w,而是s[x][y]+=w
//读入,一开始让原数组就是前缀和数组,表示原位置所有目标的价值,因为不同目标可能处在统一位置上
d. 这里存取时s[i][j]是存取的格点上的值,但计算时是按照矩形来算的
*/
四、K倍区间
1.基本思路
(1)暴力做法——时间复杂度O(n3)
//暴力做法——时间复杂度O(n3)
int res=0;
for(int r=1;r<=n;r++) //枚举区间右端点 (起点)
{
for(int l=1;l<=r;l++)//枚举区间左端点 (终点)
{ //两重循环可以把区间上所有的连续区间全部枚举到了
int sum=0;
for(int i=l;i<=r;i++) //求区间和
{
sum+=a[i];
}
if(sum%k==0) res++;
}
}
(2)前缀和优化——时间复杂度O(n2)
//前缀和优化——时间复杂度O(n2)
//第三重循环区间和可以用前缀和来做求
int res=0;
for(int r=1;r<=n;r++)
{
for(int l=1;l<=r;l++)
{
int sum=s[r]-s[l-1];
if(sum%k==0) res++;
}
}
(3)存余数——O(n) ,相当于用空间换时间
//存余数——O(n) ,相当于用空间换时间
//上述第二种方法中,第二重循环的含义为:
//当R固定时,在1~R之间找到有多少个L,满足(s[r]-s[l-1])%k==0
//相当于: 当R固定时,在0~R-1之间找到有多少个L,满足(s[r]-s[l])%k==0
//相当于: s[r]%k==s[l]%k,即问:有多少个s[l]与当前的s[r]的余数相同
//所以可以开一个数组cnt[]存一下不同余数的个数,cnt[i]表示余数是i的数有多少个
int res = 0;
cnt[0] = 1;
for (int i = 1; i <= n; i ++ )
{
res += cnt[s[i] % k];
cnt[s[i] % k] ++ ;
}
2.代码实现
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;//防止这个前缀和是可能越界的,用long long 存储
const int N = 100010;
int n, k;
LL s[N], cnt[N];//s是前缀和数组,cnt是每一个余数的个数
int main()
{
scanf("%d%d", &n, &k);
for (int i = 1; i <= n; i ++ )
{
scanf("%lld", &s[i]);
s[i] += s[i - 1];
}
LL res = 0;//这个题的答案也是有可能爆int的
cnt[0] = 1;//注意边界s[0]时
for (int i = 1; i <= n; i ++ )
{
res += cnt[s[i] % k];
cnt[s[i] % k] ++ ;
}
printf("%lld\n", res);
return 0;
}