原理

冒泡排序（Bubble Sort）是基于交换的排序，每次遍历需要排序的元素，依次比较两个相邻元素的大小，如果前一个元素大于后一个元素则两者交换，保证最后一个数字一定是最大的（假设按照从小到大排序），即最后一个元素已经排好序，下一轮只需要保证前面n-1个元素的顺序即可。
之所以称为冒泡，是因为最大/最小的数，每一次都往后面冒，就像是水里面的起泡一样。

步骤

假设从小到大排序，步骤如下：

1、从头开始，比较相邻的两个数，如果第一个数比第二个数大，那么交换它们的位置；
2、继续开始比较与其后面相邻的数，直到一轮结束后，最后一个元素的位置已经确定好；
3、除了最后一个元素以外，前面的所有未排好序的元素重复前面两个步骤；
4、重复前面1~3步骤，直到所有元素都已经排好序。

交换逻辑

例如，我们需要对数组 [98，40，34] 进行从小到大排序，每一次都需要将数组最大的移动到数组尾部。那么排序的过程如下所示：
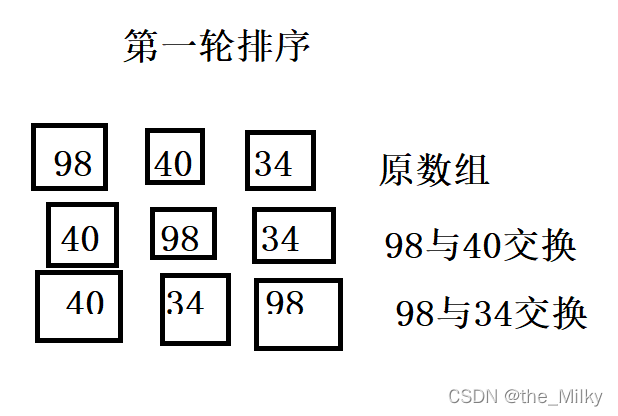
在这里插入图片描述

从上面中可以看出，总共是3个数，冒泡2次即可。

代码实现

java实现

public class BubbleSort {

    public static void main(String[ ] args) {
    int[]nums = new int[]{98,90,34,56,21};
    printf(nums);
    bubbleSort(new int[]{98,90,34,56,21});
}

    public static void printf(int[] nums) {
        for (int num : nums) {
            System.out.print(num + " ");
        }
        System.out.println("");
    }

    public static void bubbleSort(int[] nums) {
      int size = nums.length;
      // 每轮针对前面（size-i）个数进行排序
      for (int i = 0; i < size - 1; i++) {
        System.out.println("第" + (i + 1) + "轮交换开始");
        // 每一轮排序，从第 0 个元素，到 size-1-i 个元素
        for (int j = 0; j < size - 1 - i; j++) {
          // 对比相邻的两个元素
          if (nums[j] > nums[j + 1]) {
            // 元素交换。使得大的元素在后面
            int temp = nums[j+1];
            nums[j + 1] = nums[j];
            nums[j] = temp;
          }
          printf(nums);
        }
      }
    }
  }

python代码实现

class Solution:
    def printNums(self,nums):
        for i in range(len(nums)):
            print("%d" % nums[i],end=" ")
        print("")
    def bubbleSort(self,nums):
        size=len(nums)
        #每轮针对前面（size-i）个数进行排序
        for i in range(size):
            print("第",(i+1),"轮交换开始")
            for j in range(0,size-1-i):
                if nums[j]>nums[j+1]:
                    nums[j],nums[j+1]=nums[j+1],nums[j]
            self.printNums(nums)
    
if __name__=='__main__':
    solution=Solution()
    nums=[98, 90, 34, 56, 21]
    solution.printNums(nums)
    solution.bubbleSort(nums)

c++代码实现

#include <iostream>
using namespace std;

void bubbleSort(int nums[],int size);
void printf(int nums[],int size);

int main() {
    int nums[] = {98,90,34,56,21};
    int size =  sizeof(nums)/sizeof(nums[0]);
    bubbleSort(nums,size);
    return 0;
}

void bubbleSort(int nums[],int size) {
  // 每轮针对前面（size-i）个数进行排序
  for (int i = 0; i < size - 1; i++) {
    cout<<"第" <<  (i + 1) << "轮交换开始" <<endl;
    // 每一轮排序，从第 0 个元素，到 size-1-i 个元素
    for (int j = 0; j < size - 1 - i; j++) {
      // 对比相邻的两个元素
      if (nums[j] > nums[j + 1]) {
        // 元素交换。使得大的元素在后面
        int temp = nums[j + 1];
        nums[j + 1] = nums[j];
        nums[j] = temp;
      }
      printf(nums,size);
    }
  }
}

void printf(int nums[],int size){
    for (int i = 0; i < size; i++) {
        cout<<nums[i]<<" ";
    }
    cout<<endl;
}

时间复杂度与空间复杂度

从上面的代码来看，两层 for 循环嵌套，假设数组的大小为 n，那么第一轮冒泡需要比较 n-1 次，第二轮由于最后一个已经排好，需要比较 n-2 次，依次类推下一轮比较 n-3，n-4 … 直到最后只需要比较第一个元素和最后一个元素，只有 1 次比较，所以比较次数之和为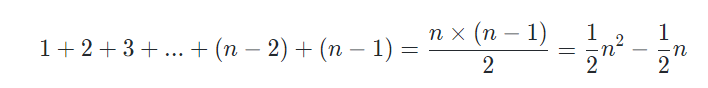：在这里插入图片描述
上面计算时间复杂度是 O(n^2 ）,时间复杂度取系数最高的项即可，当然这是最坏情况下的时间复杂度。如果这个数组已经排好序了，我们在每一轮冒泡的时候，都增加一个标识，表示是否有交换，如果没有交换，说明数组顺序已经排好，排序提前结束。这样一来，时间复杂度就是 O(n) 了，因为只遍历了第一轮的 n 个数。