单调性与极值的概念


这两个注解注意一下


极值点的判别步骤与方法
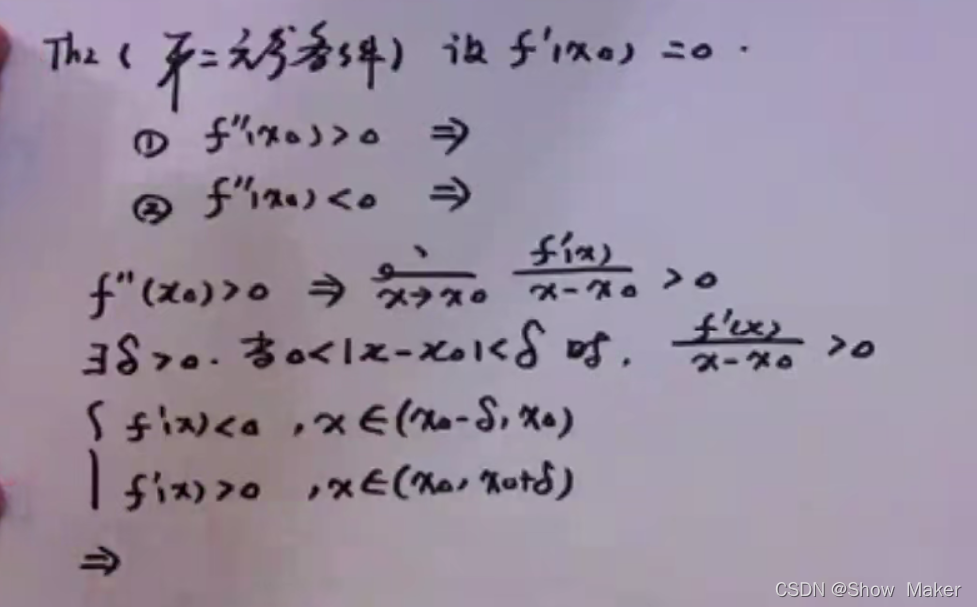
第二充分条件的证明
题型
型一

- 直接利用极限的保号性(去心邻域)
- 去心邻域左右区间分一下
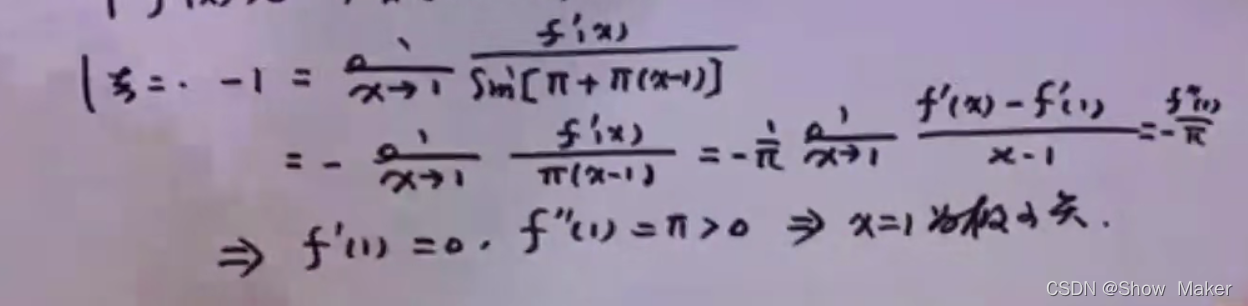
- 拆分出来,最终目的是再次利用等价无穷小凑出一个f’’(x)的定义的样子
- 这个其实挺难想的

- 观察式子得出第一个结论
- 利用这个结论再次将已经利用过的式子拆分成两个有意义的样子,再次得出一个值

- 照样根据分母等于0推出分母也等于0
- 根据极限值大于0你就可以直接用保号性了
型二 函数的零点或方程根的个数问题

这种题型的两个思路

- 先令一个f(x)
- 然后还原出一个F(x)
- 然后找出F(x)里的两个相等的点,罗尔
- 推出F`(C) =0 即f(x)等于0

- 看到是方程根的问题->弄出一个f(x)
- 反证法,设三个不同解
- 就罗尔下去,然后得到一个结论,而这个结论是不可能出现的,推出
第三种方法:单调性


解题步骤

- 给出y=f(x) 给出定义域(注意这里的定义域尽可能给得精确一些,因为后面需要对这个定义域的两个端点算出来值来进行画草图)
- 由函数导数和不可导的点推出极大值点和极大值
- 观察自变量在两个定义域端点处的变化趋势

空在那几个草图那边
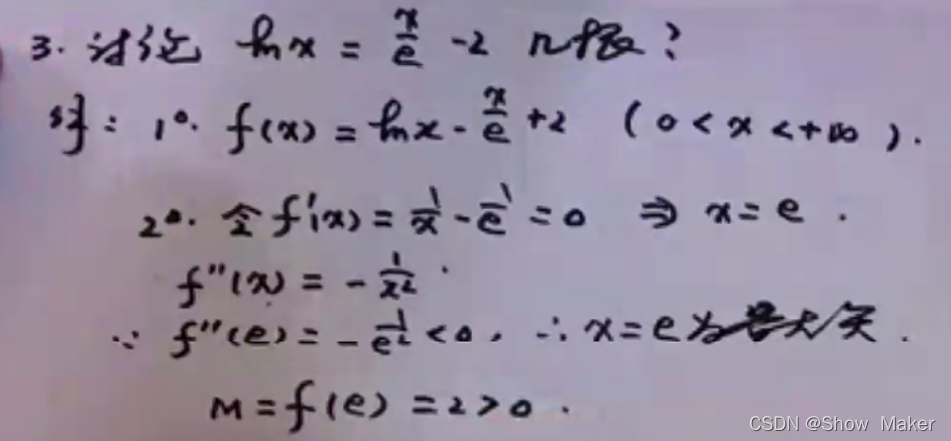
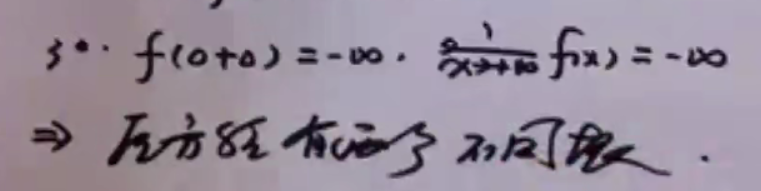
- 弄出一个函数
- 通过求一阶导,二阶导的方式弄出极大值(最大值)
- 算出两侧的值,然后结合第二步算出来的最大值来画出草图解答出题目
型三 不等式证明
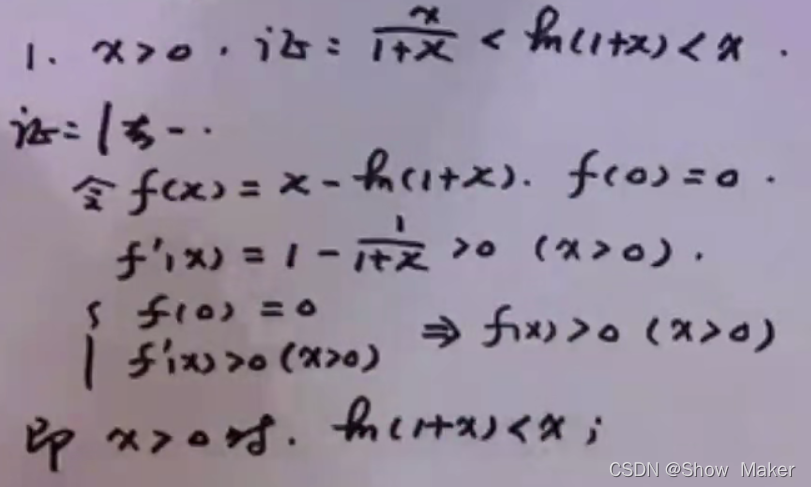

- 像这种三个不等式的,你可以尝试分开证明,一次证明一边。
- 弄出一个f(x) 尝试性地算一下f(0)的值,f`(x)的值,->足够推出东西

- 这里就稍微提一下这个思路,不要求你会,就是看到一个题目里面一个东西是另一个东西的导数的话,你就可以考虑往拉格朗日去靠了

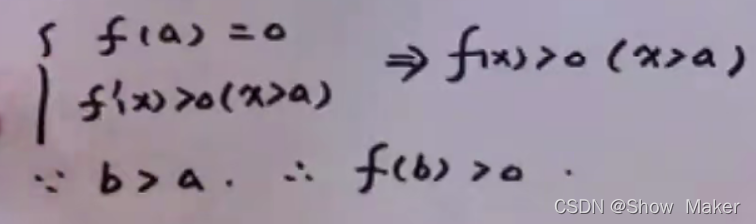
- 先找一个和结论等价的东西,用来下面构造辅助函数
- 构造辅助函数,把一个字母换成x,并且看看能不能得到一个点的值等于0
- 辅助函数求导看得不得得到一个固定大于0
- 再利用一下条件继续推


- 拉格朗日的冲动
- 初中基本不等式的冲动,当然,要熟练


- 把式子移到一边,然后把b换成x构造辅助函数
- 尝试(1.找一个点函数值为0 2.一阶求导3.二阶求导)然后推一推看