leetcode 98. 验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
-
节点的左子树只包含 小于 当前节点的数。
-
节点的右子树只包含 大于 当前节点的数。
-
所有左子树和右子树自身必须也是二叉搜索树。
示例 1:

输入:root = [2,1,3] 输出:true
示例 2:
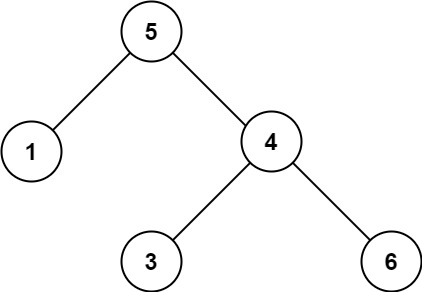
输入:root = [5,1,4,null,null,3,6] 输出:false 解释:根节点的值是 5 ,但是右子节点的值是 4 。
提示:
-
树中节点数目范围在
[1, 104]内 -
-231 <= Node.val <= 231 - 1
Related Topics
树
深度优先搜索
二叉搜索树
二叉树
思路1:非递归深度中序遍历
参考非递归的中序遍历,在每一次遍历的时候,跟前一个值比较大小。
class Solution {
? ?public boolean isValidBST(TreeNode root) {
? ? ? ?//中序非递归遍历二叉树 和前一个值进行比较
? ? ? ?Deque<TreeNode> stack = new LinkedList<>();
? ? ? ?List<Integer> list = new ArrayList<>();
?
? ? ? ?TreeNode p = root;
? ? ? ?while (p!= null || !stack.isEmpty()){
? ? ? ? ? ?if(p!=null){
? ? ? ? ? ? ? ?stack.push(p);
? ? ? ? ? ? ? ?p = p.left;
? ? ? ? ? }else{
? ? ? ? ? ? ? ?p = stack.pop();
? ? ? ? ? ? ? ?//跟前一个比较 必须大于前一个值 但由于第一个元素前面没有值 必须保证下标
? ? ? ? ? ? ? ?if(list.size()>0&& list.get(list.size()-1) >= p.val){//不符合
? ? ? ? ? ? ? ? ? ?return false;
? ? ? ? ? ? ? }
? ? ? ? ? ? ? ?list.add(p.val);
? ? ? ? ? ? ? ?p = p.right;
? ? ? ? ? }
? ? ? }
? ? ? ?return true;
? }
}
解答成功:
执行耗时:3 ms,击败了18.39% 的Java用户
内存消耗:41.4 MB,击败了5.09% 的Java用户
可以把集合改成一个最小值min记录。
public boolean isValidBST(TreeNode root) {
? ?//中序非递归遍历二叉树 和前一个值进行比较
? ?Deque<TreeNode> stack = new LinkedList<>();
? ?long min = Long.MIN_VALUE;
?
? ?TreeNode p = root;
? ?while (p!= null || !stack.isEmpty()){
? ? ? ?if(p!=null){
? ? ? ? ? ?stack.push(p);
? ? ? ? ? ?p = p.left;
? ? ? }else{
? ? ? ? ? ?p = stack.pop();
? ? ? ? ? ?//跟前一个比较 必须大于前一个值 但由于第一个元素前面没有值 必须保证下标
? ? ? ? ? ?if(min >= p.val){//不符合
? ? ? ? ? ? ? ?return false;
? ? ? ? ? }
? ? ? ? ? ?min = p.val;
? ? ? ? ? ?p = p.right;
? ? ? }
? }
? ?return true;
}
解答成功:
执行耗时:1 ms,击败了28.67% 的Java用户
内存消耗:41.4 MB,击败了5.09% 的Java用户
思路2:递归
根据当前值,确定左子树中值的范围,在递归中根据值的范围判断是否符合。
class Solution {
? ?public boolean isValidBST(TreeNode root) {
? ? ? ?return isValidBST(root,Long.MIN_VALUE,Long.MAX_VALUE);
? }
? ?//(low,high)为这颗树的范围 这个树种的值都必须满足 low < val < high
? ?//low high为long型是因为测试用例有整型最小值 测试用例:[-2147483648]
? ?public boolean isValidBST(TreeNode root,long low,long high){
? ? ? ?if(root == null){
? ? ? ? ? ?return true;
? ? ? }
? ? ? ?if(root.val <= low || root.val >= high){
? ? ? ? ? ?return false;
? ? ? }
? ? ? ?//左子树中值的范围是 (low,当前节点的值)
? ? ? ?//右子树中值的范围是(当前节点的值,high)
? ? ? ?return isValidBST(root.left,low,root.val) && isValidBST(root.right,root.val,high);
? }
}