[数据结构与算法]欧拉角推算旋转矩阵的问题

旋转的正方向

我们在进行旋转的时候，我们首先得知道怎么是一个正方向，正方向是遵循右手定则的，即：右手握住对应的旋转轴，大拇指指向正方向，那么四根手指指向的方向就是正方向了。

接下来我们引入公式

//在右手系中绕X轴旋转p° 对应的矩阵Rx
        | 1    0        0 |
  Rx=   | 0   cosp   -sinp|
        | 0   sinp    cosp|
//在右手系中绕Y轴旋转h° 对应的矩阵Ry
        | cosh   0   sinh|
  Ry=   |  0     1     0 |
        |-sinh   0   cosh|
//在右手系中绕Z轴旋转b° 对应的矩阵Rz
        |cosb  -sinb   0 |
  Rz=   |sinb   cosb   0 |
        |  0     0     1 |

如果对这个推算感兴趣可以参考牛小骥老师的课件：

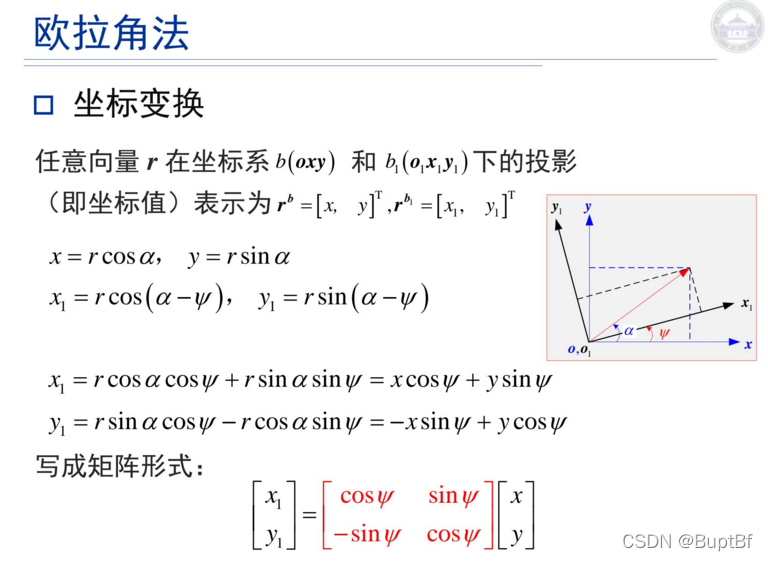
也就是这个转化矩阵只要你是右手系就可以正常使用，不论你是使用下面谁的坐标系：

• 右前上-东北天（西北工业大学严老师团队）
• 前右下-北东地（武汉大学牛老师团队）

都是可以正常使用的。

旋转顺序的问题

根据组合旋转矩阵的定义也可以了解，多次旋转组合在一起，例如Z-X-Y顺规的欧拉角(30°，62°，28°)就是先绕Z轴旋转28°，然后绕X轴旋转30°，最后绕Y轴旋转62°。单一的旋转矩阵无法满足这样的组合旋转，无法完成对应。此时就需要利用旋转变换的性质：物体绕轴旋转对应的矩阵具有可累乘的性质，即多一次旋转就是多一次矩阵乘法。

因此，组合旋转矩阵就是对应顺序的基础旋转矩阵的乘积。例如Z-X-Y顺规的欧拉角对应的组合旋转矩阵就是R = RzRxRy。如果是X-Y-Z顺规的欧拉角，对应的组合旋转矩阵就是R = RxRyRz。依据这个乘法法则即可获得欧拉角→旋转矩阵的转换。

举一个例子，按照2.1节中的基础旋转矩阵，计算Z-X-Y顺规下对应的旋转矩阵，其结果如下：

//欧拉角(p,h,b)在右手系中对应的旋转矩阵（Z-X-Y顺规）
               |cosbcosh-sinbsinpsinh  -sinbcosp  cosbsinh+sinbsinpcosh|
R = Rz*Rx*Ry = |sinbcosh+cosbsinpsinh   cosbcosp  sinbsinh-cosbsinpcosh|
               |     -cospsinh            sinp           cospcosh      |

安卓的欧拉角怎么转化旋转矩阵