摆动序列

leetcode链接

解法

题目可以理解为：在不改变给定nums序列的顺序的情况下，找到一个最长的摆动序列。（摆动序列是指每相邻的两个数的差值是正负交替的），如果画出图来，该序列会呈现一个锯齿状。
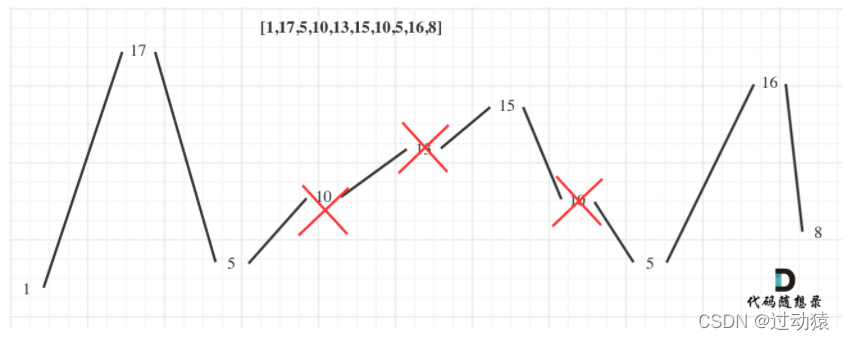
在这里插入图片描述
贪心策略为：

局部最优：在不改变单调性的情况下，找到距离当前数最远的一个数值。（比如选1，单调性先是增大，所以再选17，然后单调性变为减小，然后再选5，然后单调性变为增大，此时有10，13，15三个数，选择距离5最远的，所以选择15…）这样选择可以保证下一个数有足够大的空间可以选择（比如选完5之后选15，因为如果选10的话，后面的13、15也还是不能选的，选择13的话，后面的15也是不能选的，所以不如直接选15，给后面递减时相对大的空间可以选择数值（比15小的数肯定要比比13小、比10小的数要多））

整体最优：每次都保证有足够大的空间可以选择数值，那么整体来看就能选择更多的数字，即序列更长。

上述思想反映到图上就是：统计每次单调性变换之后取得的峰值的个数即可

代码思路：

首先先要将nums前面相等的数值都剔除掉，因为相等的数字不能构成摆动序列，比如(1,1,1,1,7,2)实际上和(1,7,2)一样。保证刚开始的单调性可得。

index = 0
while index<len(nums)-1:
    if nums[index]==nums[index+1]:
        index += 1
    else:
        break
nums = nums[index:]

然后分情况讨论：

len(nums)<=2: 该情况下只有len(nums)==0，len(nums)==1和len(nums)==2，而对于长度为0而言就返回0，对于长度为1而言就返回1，对于长度为2而言就返回2，所以返回len(nums)即可。
len(nums)>2: 需要一个sum来计数，还需要一个flag来代表单调性，1为递增，-1为递减，然后遍历nums去统计峰值即可。

if len(nums)<=2:
    return len(nums)


sum = 1 # 初始化为1是因为最开始的位置就是一个峰值
flag = 1 # 初始化为递增
if nums[0]>nums[1]: # 如果刚开始是递减
    flag = -flag # 则变为递减

for i in range(len(nums)-1):
    if flag==1 and nums[i]<nums[i+1]: # 如果当前flag==1并且的确是递增nums[i]<nums[i+1]，表示单调性没变化，所以不用操作
        continue
    if flag==1 and nums[i]>nums[i+1]: # 如果当前flag==1并且nums[i]>nums[i+1]，表示单调性变化，所以统计一个峰值,sum+=1，单调性变化
        sum += 1
        flag = -flag

    if flag==-1 and nums[i]>nums[i+1]: # 同上
        continue
    if flag==-1 and nums[i]<nums[i+1]:
        sum+=1
        flag = -flag

sum += 1 # 统计最后一个数字，也是一个峰值

整体代码：

def wiggleMaxLength(nums):

    index = 0
    while index<len(nums)-1:
        if nums[index]==nums[index+1]:
            index += 1
        else:
            break

    nums = nums[index:]


    if len(nums)<=2:
        return len(nums)
        
    sum = 1
    flag = 1
    if nums[0]>nums[1]:
        flag = -flag

    for i in range(len(nums)-1):
        if flag==1 and nums[i]<nums[i+1]:
            continue
        if flag==1 and nums[i]>nums[i+1]:
            sum += 1
            flag = -flag

        if flag==-1 and nums[i]>nums[i+1]:
            continue
        if flag==-1 and nums[i]<nums[i+1]:
            sum+=1
            flag = -flag

    sum += 1

    return sum