[数据结构与算法]AcWing 1112. 迷宫（内部搜索无需回溯）

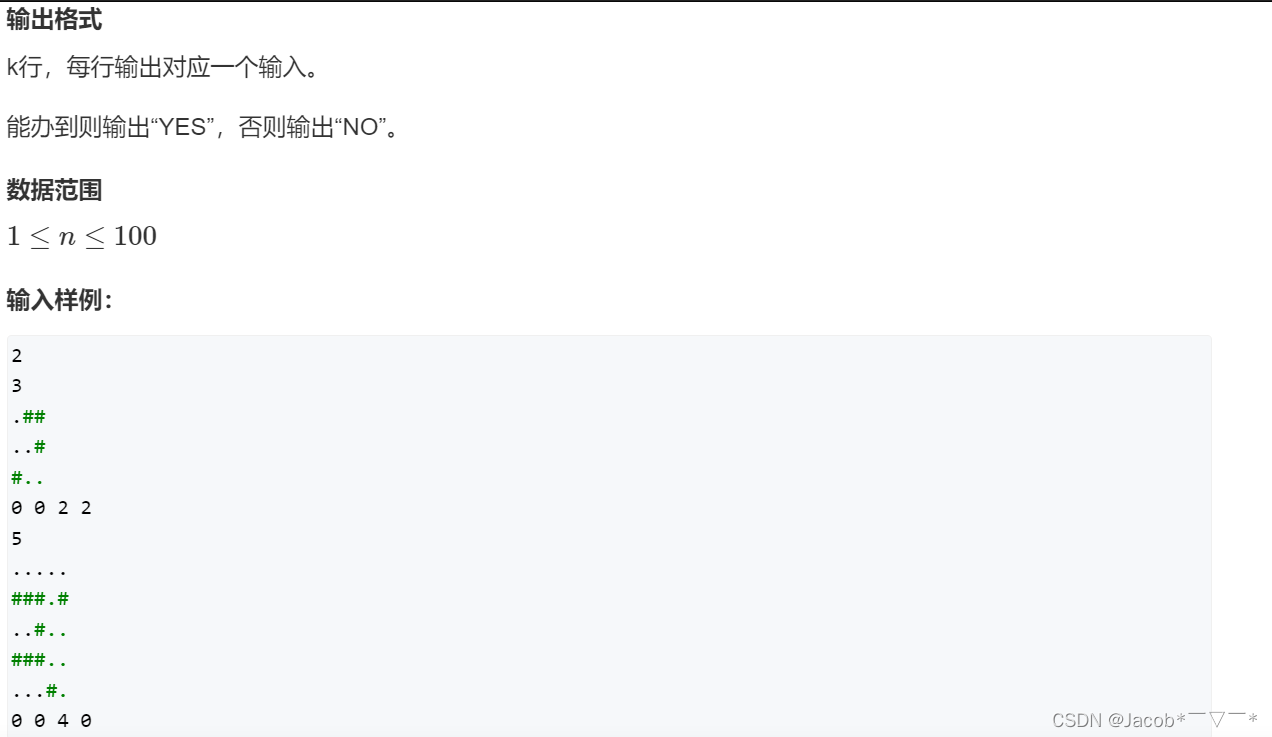
内部搜索不用（能）回溯，外部搜索才需要（必须）回溯和恢复现场

只对细节进行分析：

为什么不需要恢复现场呢(st[x][y]=false)？

“因为st[x][y]标记当前点(x,y)被搜索到,当你恢复现场的时候,假设你是从(px,py)搜到点(x,y)的时候,你在判断(x,y)可以被(px,py)到达之后已经将(x,y)计数一次,当你下次再从某个(px2,py2)搜到(x,y)的时候,此时要通过st[x][y]判重,如果你恢复现场,那么你将再从将(x,y)进行重复搜索,容易TLE,所以不要恢复现场”（与马走日进行对比）

要注意把判断障碍物的if(g[x][y]==’#’) return false; 放到循环外写，因为可能终点在障碍物上

1.循环里应该是if(dfs(a,b)==true) return true; 而不能是dfs(a,b)，因为下一层的返回true之后，这一层也要紧跟着直接返回true

2.不需要回复现场，即不需要st[a][b]=false要一直往下走，因为该题不是枚举所有方案，因此回复现场会超时！！

时间复杂度：

算法 BFS/DFS 均是 O(n^2)
注：DFS无需回溯，即无需st[x][y]=false;

分析：
需遍历每个点，所以时间复杂度为O(n^2)

#include<bits/stdc++.h>
using namespace std;
const int N = 110;
char g[N][N];
bool st[N][N];
int n,k;
int ha,la,hb,lb;

bool dfs(int x,int y)
{
    if(g[x][y]=='#') return false;
    //返回false代表此路不可达,但不是代表所有路不可达,返回之后就递归回到上一层,继续之前那一层的寻路(对滴)
    if(x==hb&&y==lb) return true;
    int dx[]={1,0,-1,0},dy[]={0,1,0,-1};
    st[x][y]=true;
    for(int i=0;i<4;++i)
    {
        int a=x+dx[i],b=y+dy[i];
        if(a<0||a>=n||b<0||b>=n) continue;
        if(st[a][b]) continue;
        if(dfs(a,b)) return true;
    }
    return false;
}

int main()
{
    cin>>k;
    while(k--)
    {
        cin>>n;
        for(int i=0;i<n;++i)
        {
            cin>>g[i];
        }
        memset(st,false,sizeof st);
        cin>>ha>>la>>hb>>lb;
        if(dfs(ha,la)) cout<<"YES"<<endl;
        else cout<<"NO"<<endl;
    }
    return 0;
}