[数据结构与算法]Leetcode-542. 01 矩阵

链接

542. 01 矩阵

题目

给定一个由 0 和 1 组成的矩阵 mat?，请输出一个大小相同的矩阵，其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。

两个相邻元素间的距离为 1 。

示例

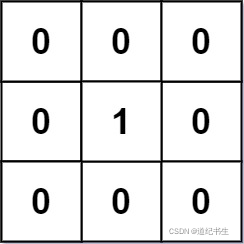
示例 1：
输入：mat = [[0,0,0],[0,1,0],[0,0,0]]
输出：[[0,0,0],[0,1,0],[0,0,0]]

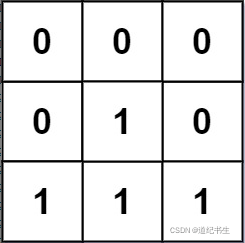
示例 2：
输入：mat = [[0,0,0],[0,1,0],[1,1,1]]
输出：[[0,0,0],[0,1,0],[1,2,1]]

说明

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 10e4
• 1 <= m * n <= 10e4
• mat[i][j] is either 0 or 1.
• mat 中至少有一个 0?

思路一（BFS）

我们可以先假设整个矩阵中只有一个0，那么只要从这个0开始进行广度优先搜索，这个0上下左右的1的距离全部为1，然后再外面一圈的1的距离全为2...以此类推。但该题矩阵中的0的个数不止一个而是有多个，这种情况下，我们就可以假设还存在一个超级0，所有的0到都是由这个超级0通过广度优先搜索搜到的，只不过他们的距离不是1而是0，这样就转化成了前面只有1个0的情况。

而具体的做法就是将所有的0的位置全都添加都队列当中，逐一进行广度优先搜索，依次减第二层，第三层搜索到的位置再次添加到队列当中进行广度优先搜索，每一轮距离+1。

C++ Code

class Solution {
public:
    vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
        int m=mat.size();
        int n=mat[0].size();
        vector<vector<int>> dist(m,vector<int>(n,0));
        vector<vector<bool>> view(m,vector<bool>(n,0));
        queue<pair<int, int>> q;
        for(int i=0;i<m;i++)
            for(int j=0;j<n;j++)
                if(mat[i][j]==0)
                {
                    view[i][j]=true;
                    q.emplace(i, j); //先将所有值为0的坐标加入到队列
                }

        int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
        while(!q.empty())
        {
            auto [x,y]=q.front();
            q.pop();
            for(int i=0;i<4;i++)
            {
                int nx=x+dirs[i][0];
                int ny=y+dirs[i][1];
                if(nx>=0 && ny>=0 &&nx<m &&ny<n &&!view[nx][ny])
                {
                    dist[nx][ny]=dist[x][y]+1;
                    view[nx][ny]=true;
                    q.emplace(nx, ny);
                }
            }
        }
        return dist;
    }
};

?

?