1、回溯算法介绍
参考:代码随想录
1. 定义
回溯算法是一种搜索算法,回溯是递归的副产品,只要有递归就有回溯,回溯函数就是递归函数,对于回溯的优化就是剪枝
回溯是在集合中递归搜索,回溯问题可以抽象为树形结构,集合的大小构成了树的宽度(for循环),递归的深度构成了数的深度
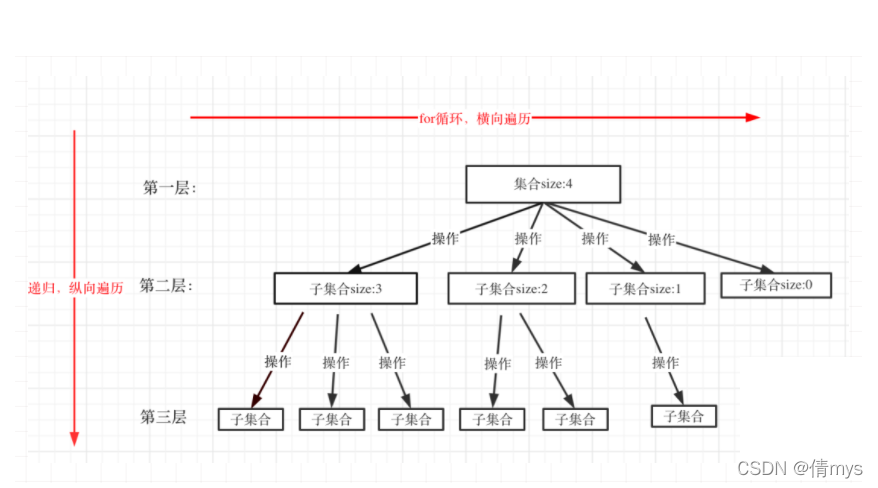
2. 可解决的问题
- 组合问题:n个数中按一定规则找出k个数的集合
- 排列问题:n个数中按一定规则全排列
- 切割问题:一个字符串按一定规则切割
- 子集问题:n个数的集合中符合条件的子集
- 棋盘问题:n皇后,数独
3. 回溯的模板
void backreacking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合元素(树中节点孩子的数量就是结合的大小)) {
处理节点;
backreacking(路径,选择列表);//递归函数
回溯,撤销处理结果;
}
}
2、组合问题
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。1 <= n <= 20;1 <= k <= n
示例 1:
输入:n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
组合问题抽象为树形结构:
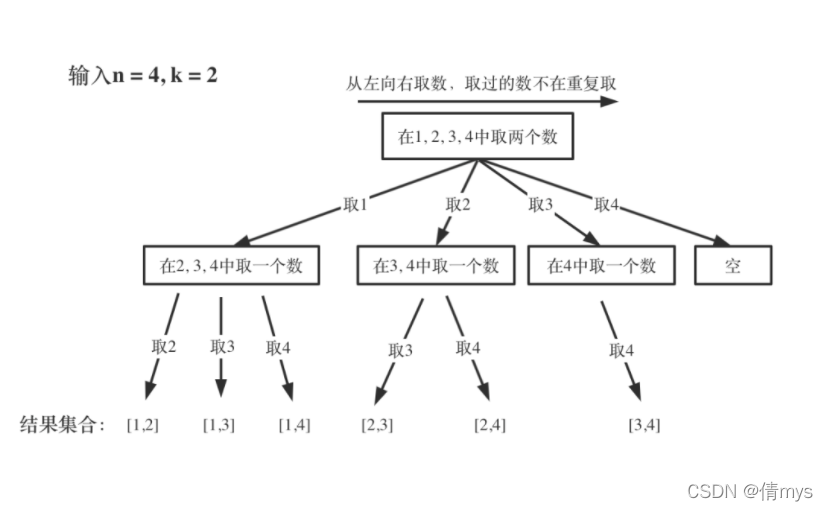
代码:
public class combine {
public List<List<Integer>> combine(int n, int k) {
List<List<Integer>> res = new ArrayList<>();
backtracking(n, k, 1, new ArrayList<Integer>(), res);
return res;
}
/**
* 回溯函数/递归函数
* @param n 数的范围是 1-n
* @param k 求k个数的组合
* @param startIndex for循环每次从startIndex开始遍历 题目要求从1开始
* @param path 存放取到的节点i
* @param res 返回值
*/
void backtracking(int n, int k, int startIndex, List<Integer> path, List<List<Integer>> res) {
if (path.size() == k) {//此时path存放的数刚好是需要的组合
res.add(new ArrayList<>(path));//加入到res的List中进行返回
return;
}
//处理节点
for (int i = startIndex; i <= n; i ++) {
path.add(i);//处理节点
backtracking(n, k, i + 1, path, res);//递归
path.remove(path.size() - 1);//回溯,撤销处理的节点
}
}
}
对回溯算法进行剪枝优化,效率会提升很多,一下使用leetcode的77题组合进行的测试结果:
- 不用剪枝:

- 使用剪枝:

剪枝的树形结构:
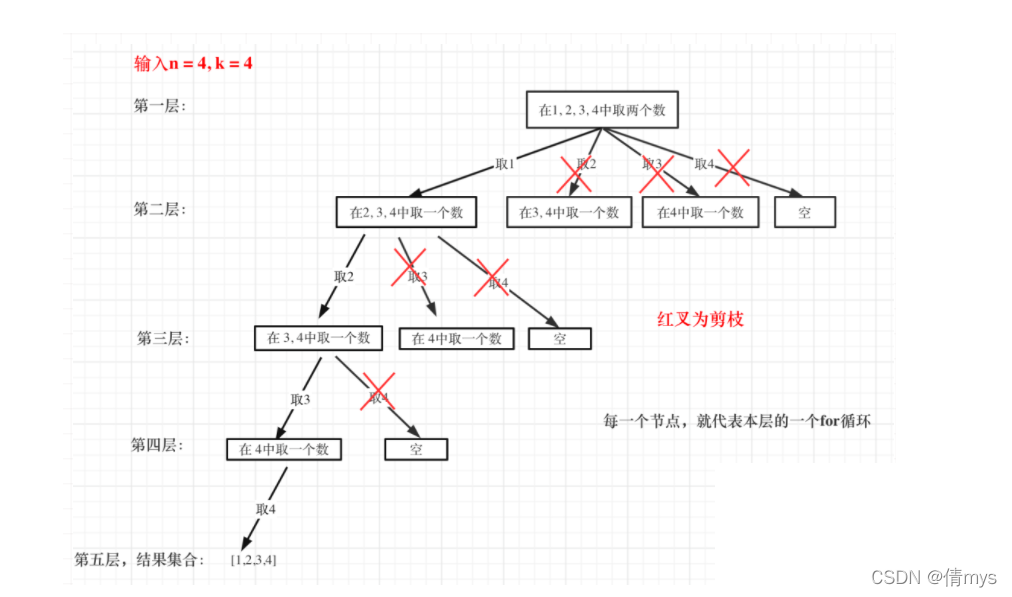
当n=4,k=4时,第一层for循环,从元素2开始的遍历没有意义;第二层for循环,从元素3开始的遍历没意义了
优化过程: - 已经选择的元素个数:path.size()
- 还需要的元素个数:k - path.size()
- 集合n中至少从位置:n - (k - path.size()) + 1开始遍历 (+1是因为需要包括起始位置)
优化后的代码:
//剪枝优化
void backtracking2(int n, int k, int startIndex, List<Integer> path, List<List<Integer>> res) {
if (path.size() == k) {//此时path存放的数刚好是需要的组合
res.add(new ArrayList<>(path));//加入到res的List中进行返回
return;
}
//处理节点
for (int i = startIndex; i <= n - (k - path.size()) + 1; i ++) {
path.add(i);//处理节点
backtracking(n, k, i + 1, path, res);//递归
path.remove(path.size() - 1);//回溯,撤销处理的节点
}
}
注意:剪枝的思路就是for循环遍历时,n的范围
未完待续…