[数据结构与算法]状态压缩DP讲义

• 动态规划随着阶段增长，在每个状态维度上会不断扩展；任意时刻已求解状态和尚未求解的状态在各个维度上的分界点组成DP扩展的轮廓。对于某些问题，我们需要在动态规划的“状态”中记录一个集合，保存这个“轮廓”的详细信息，以便进行状态转移。 若集合大小不超过N，集合中每个元素都是小于K的自然数，则我们可以把这个集合看作一个N位K进制数，以一个$[O,K^{N?1}]$之间的十进制整数的形式作为DP状态的一维。
• 状态压缩DP：将集合转化为整数记录在DP状态中的一类算法。
• 使用条件：一般能够采用状态压缩dp的题目数据规模都不大（<30），这是判断是否能够采用状态压缩dp的一个重要条件。

博客中大部分例题测试数据均为笔者生成的随机数据，若数据太弱或有错请留言评论；另外本博客参考了李煜东的《算法竞赛进阶指南》课本和周伟的《状态压缩》论文。

我不生产知识，我只是个知识的搬运工！！！

一. 棋盘类状压DP

引例

在n*n(n≤20)的方格棋盘上放置n个车(可以攻击所在行、列)，求使它们不能互相攻击的方案总数。

组合数学：一行一行的放，则第一行有n种选择，第二行n-1，……，最后一行只有1种选择，根据乘法原理，答案就是n!
状态压缩：一行一行的放，并取每列是否放置了棋子作为状态；某一列如果已经放置棋子则为1，否则为0。这样，一个状态就可以用一个最多20位的二进制数表示。例如n=5，且第1、3、4列已经放置，则这个状态可以表示为01101(从右到左)。设fs为达到状态s的方案数，则可以尝试建立f的递推关系。
考虑n=5，s=01101；状态中有3个1，即有3行放置了棋子，因为是一行一行放置的，所以达到s时已经放到了第三行。一行只能放一个车，则第三行的车只有三种情况（第1列、第3列或第4列）：

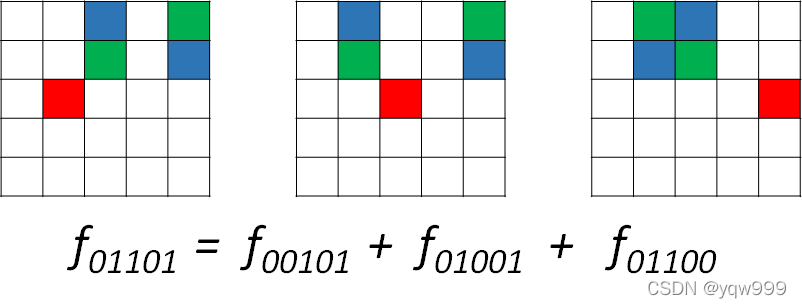
根据上面的讨论思路推广之，得到引例的解决办法：
$f_0=1$
$f_s=\sum f_{s?2^i}$，其中s从右往左数（从0开始）第i位二进制位为1
核心代码如下：

dp[0]=1;//其他值均为0 
for(int s=1;s<(1<<n);s++)//枚举所有可能的状态0--2^n-1 
	for(int i=0;i<n;i++)//枚举s的每个二进制位 
		if((s>>i)&1)//如果s的第i个位置是1则转移 
			dp[s]+=dp[s-(1<<i)]; 
cout<<dp[(1<<n)-1];

反思这个算法，其正确性毋庸置疑(可以和$n!$对比验证)
但是算法的时间复杂度为O($n?2^n$)，空间复杂度O($2^n$)，是个指数级的算法，比用循环O(n)时间复杂度计算n!差的多，它有什么优势？

答案是：可扩展性，具体的可以看看以下的例题

例1

【题目描述】
在$n?n(n\le 20)$的方格棋盘上放置n个车，某些格子不能放，求使它们不能互相攻击的方案总数。
【输入描述】
一个$n?n$的矩阵maze， 如果maze[x][y]为0表示该位置不能放，如果为1则能放

• 组合数学+容斥原理——复杂。
• 状态压缩：和引例一样，逐行放置，不同点在于有些格子不能放；引例的实质是枚举状态s中的1进行转移，因此对于此题只要枚举的同时判断该位置是否可放即可。
• 算法优化：
  (1). 将棋盘的第i行是否能放的二进制数（能1不能0），压缩为一个十进制数，得到状态g[i]。设ts=s & g[i]，枚举ts中的1即可，g[i]会将s中不能放的位置中的1消除。例如：$s=(100110{)}_2，g[i]=(100011{)}_2则ts=(100010{)}_2$
  (2).应用lowbit寻找二进制中的1，加快转移速度

例2

【题目描述】U204450
在$n?m(n,m\le 20)$的方格棋盘上放置k个车，有的位置不能放，求使它们不能互相攻击的方案总数。
【输入描述】
一个$n?m$的矩阵maze ，如果maze[x][y]为0表示该位置不能放，如果为1则能放

和例1类似，不同点在于这里是$n?m$的棋盘，只放k个车；$k>min(n,m)$时方案数一定为0。将i行能放或不能放压缩为一个整数can[i]；逐行考虑，每行可能放0个或1个车，状态将和放置车的个数有关

• 状态定义：f[i][j][s]表示前i行放j个车，且它们的放置状态为s时的方案数
• 状态转移：
  若第i行不放，f[i][j][s]=f[i-1][j][s]
  若第i行放1个，枚举t=s&can[i]二进制位中的1，t中的每个1都有可能是第i行放的；$f[i][j][s]=\sum f[i?1][j?1][t?2^x]$其中t的第x位为1
• 边界条件：前i行放0个车，则状态一定为0，此时方案数为1，即f[i][0][0]=1
• 目标状态：f[n][k][含有k个1的所有s]
• 时空优化：空间上可以数组滚动优化，预处理包含j个1的s有哪些

#include<bits/stdc++.h>
using namespace std;
const int N=21;
int n,m,k,ans,can[N],f[2][N][1<<N];
int lowbit(int x){return x&(-x);}
int calOne(int x){//计算状态x的二进制位中有多少个1
	int cnt=0;
	while(x)cnt++,x-=lowbit(x);
	return cnt;
}
vector<int>sta[N];
int main(){
	scanf("%d%d%d",&n,&m,&k);
	for(int i=1;i<=n;i++)
		for(int j=1,x;j<=m;j++){
			scanf("%1d",&x);
			can[i]|=(x<<(j-1));
		}
	for(int s=0,ms=1<<m;s<ms;s++)
		sta[calOne(s)].push_back(s);
	f[1][0][0]=f[0][0][0]=1;//前i行放0个状态为0时的方案数为1
	for(int i=1;i<=n;i++){
		for(int j=1;j<=min(i,k);j++){
			for(int x=0;x<sta[j].size();x++){
				int s=sta[j][x];
				f[i%2][j][s]=f[(i-1)%2][j][s];
				int t=s&can[i];
				while(t)
					f[i%2][j][s]+=f[(i-1)%2][j-1][s-lowbit(t)],t-=lowbit(t);
			}
		} 
	}
	for(int x=0;x<sta[k].size();x++)ans+=f[n%2][k][sta[k][x]];
	printf("%d",ans);
	return 0;
} 

例3

【题目描述】U204630
有一个$n?m$的棋盘($n,m\le 80,n?m\le 80$)要在棋盘上放k(k<80)个棋子，使得任意两个棋子不相邻；且有些格子不能放，求合法的方案总数。
【输入描述】
输入n,m,k
【输出描述】
合法的方案总数

• 数据规模：n×m≤80，似乎不适合状态压缩求解，$2^{80}$时间和空间都无法承受
• 隐含条件：9*9=81>80，则n，m不可能同时大于9；因此，min(n,m)≤8。若m>n，交换m和n（相当于棋盘旋转90°）；每行的状态可以用m位的二进制数表示，然后逐行放置。（状态总数为$2^m$，所以要让m尽量小）
• 行限制：每行可以放0到$m/2$ 个棋子，只要棋子放定则第i行状态$S_i$便确定；
• 列限制：放第i行时需要与第i-1行比较，若$S_i$ & $S_{i?1}==0$则该组合是可行的，对于确定的$S_i$需要枚举其对应的组合$S_{i?1}$，然后采用加法原理相加。因此$S_i$应该设计到状态中去。
• 棋子放置个数不得超过k，因此放置棋子的个数也应该设计到状态中去。
• 状态设计：$f[i][j][S_i]$表示前i行共放置j个棋子，且第i行棋子状态为$S_i$时的方案数。
• 目标状态：$f[n][k][所有满足条件的S]$
• 状态转移：$f[i][j][S_i]=\sum f[i?1][j?状态S_i中1的个数][S_{i?1}]，其中S_i$ & $S_{i?1}==0$
• 空间优化1：滚动数组，将维度i滚动掉
• 时间优化1：预处理(DFS或子集枚举)出满足行限制的状态集合S，并记录每个元素$S_i$中含有多少个1
• 空间优化2：预处理会去掉很多无用状态，可缩小第3个维度；将状态重新设计为f[i][j][k]表示前i行共放置j个棋子，且第i行棋子状态为$S_k$时的方案数。
• 时间复杂度为$O(n\times k\times (2^m{)}^2)$，即$O(n\times k\times 4^m)$；空间复杂度$O(k\times 2^m)$

#include<bits/stdc++.h>
using namespace std;
const int N=100;
long long n,m,k,ans,cnt,s[1<<10],c[1<<10],f[2][N][1<<10];
int lowbit(int x){return x&(-x);}
int calOne(int x){
	int z=0;
	while(x)z++,x-=lowbit(x);
	return z;
}

int main(){
	scanf("%lld%lld%lld",&n,&m,&k);
	if(n<m)swap(n,m);
	for(int i=0,ms=1<<m;i<ms;i++)
		if((i&(i<<1))==0)
			s[cnt]=i,c[cnt++]=calOne(i);
	f[0][0][0]=1;
	for(int i=1;i<=n;i++)
		for(int x=0;x<cnt;x++)
			for(int j=c[x];j<=k;j++){
				f[i%2][j][x]=0;
				for(int y=0,now=i%2,pre=now^1;y<cnt;y++)
					if((s[x]&s[y])==0)
						f[now][j][x]+=f[pre][j-c[x]][y];
			}
	for(int x=0;x<cnt;x++)ans+=f[n%2][k][x];
	printf("%lld",ans);
	return 0;
} 

DFS直接生成有效状态，比枚举二进制检验更高效。

void dfs(int state,int p,int count1){//当前状态，位置，1的个数 
	if(p>m){ //位置枚举完了 
		s[cnt]=state,c[cnt++]=count1; 
		return ; //返回上一个位置执行下一种方案。 
	} 
	dfs(state,p+1,count1);//当前位置不放 
	dfs(state+(1<<(p-1)),p+2,count1+1);//当前位置放，则下一个位置不能放 
}

例4：炮兵阵地

【题目描述】P2704
n*m的棋盘(n≤100,m≤10)，有的地方能放棋子有的地方不能放，求在棋盘上最多能放多少个棋子，使得相邻棋子之间最少间隔2个位置。
【输入描述】
第一行N M
接下来N行，每行M个字符（P/H）中间没有空格，P表示能放，H表示不能放
【输出描述】
仅一行，包含一个整数K，表示最多能摆放的炮兵部队的数量。

【解法1】

• 从上到下逐行处理，将棋盘第i行是否能放的情况压缩为一个二进制数g[i]（H=1 , P=0）
• 预处理出所有满足行限制的状态集合S，并记录每个状态中二进制1的个数；经测试|S|≤60
• 状态分析：向第i行转移时，需要知道第i-1行和第i-2行的状态。例3向第i行转移时，需要知道第i-1行状态；例3是保存第i行放置状态枚举第i-1行的放置状态；因此这里可以考虑保存第i行和第i-1行的放置状态枚举第i-2行的状态。
• 状态定义：$f[i][S_i][S_{i?1}]$表示第i行放置状态为$S_i$且第i-1行放置状态为$S_{i?1}$时最多能放多少个炮兵。
• 状态转移：$f[i][S_i][S_{i?1}]$ = max{ $f[i?1][S_{i?1}][S_{i?2}]$ + $S_i$的二进制中1的个数 }
• 转移条件：$S_i$&$S_{i?1}=0,S_{i?1}$&$S_{i?2}=0，S_i$&$g_i=0，S_{i?1}$&$g_{i?1}=0$
• 边界条件：$f[0][0][0]=0$，其余都为负无穷
• 目标状态：第n行放置状态不确定，因此应该是在满足条件的所有状态中取最大值。
• 时间复杂度$O(n\times |S{|}^3)$，空间复杂度$O(n\times |S{|}^2)$，经测试$|S|<60$
  题目的状态规模本来是 $O(N\times 4^M)$，通过预处理排除掉不合法的状态，使解法变得高效。

#include<bits/stdc++.h>
using namespace std;
const int N=105,M=500,inf=-1e9;
int n,m,ans,g[N],cnt,s[M],c[M],f[N][M][M];
void dfs(int sta,int p,int one){
	if(p>m){
		s[cnt]=sta,c[cnt++]=one;
		return;
	}
	dfs(sta,p+1,one);
	dfs(sta|(1<<(p-1)),p+3,one+1);
}

int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++){
			char x=getchar();
			while(x!='P'&&x!='H')x=getchar();
			g[i]=(g[i]<<1);
			if(x=='H')g[i]|=1;
		}
	dfs(0,1,0);
	memset(f,0x9f,sizeof(f));
	f[0][0][0]=0;
	for(int i=1;i<=n;i++)
		for(int si=0;si<cnt;si++)
			if((s[si]&g[i])==0)
				for(int sj=0;sj<cnt;sj++)
					if((s[si]&s[sj])==0&&0==(s[sj]&g[i-1]))
						for(int sk=0;sk<cnt;sk++)
							if((s[si]&s[sk])==0){
								f[i][si][sj]=max(f[i][si][sj],f[i-1][sj][sk]+c[si]);
								if(i==n)ans=max(ans,f[i][si][sj]);
							}
	printf("%d",ans);
	return 0;
} 

【解法2】《算法竞赛进阶指南》P303

• 仍以“行”作为动态规划的阶段，但用更高进制的状态压缩代表一行的状态，从而区分网格中不同位置的不同属性。
• 根据题意，一个格子放置炮兵以后，该格子上下两行的同一列都不能再放置炮兵。可以用数字2表示放置炮兵的格子，规定2的下面必须是1，1的下边必须是0，只有0的下边可以放置新的炮兵。在炮兵不会误伤的情况下，每个“十字”攻击范围形如:

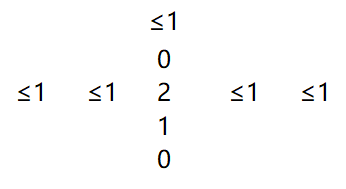
• 把每行的状态压缩为一个M位三进制数，用$03^M?1$之间的十进制整数存储。
• 问题转换为放第i行的炮兵需要知道第i-1行的状态，类似例3
• 状态设计：$f[i][S_i]$表示第i行压缩状态为$S_i$时最多能放炮兵的数量
• 状态转移：对于每个合法状态$f[i][S_i]$考虑他能转移到哪些状态？等价于考虑第i+1行的每个位置填什么数字，需要四个条件：

(1). 若第i行第j列为2，则第i+1行第j列必须填1
(2). 若第i行第j列为1，则第i+1行第j列必须填0
(3). 山地不能填2
(4). 填2的格子的左右两个格子都不能填2

• 像本题这种状态表示比较复杂、冗余较多的题目，我们不一定非要写出确切的状态转移方程。可以通过深度优先搜索(DFS)，在保证上述四个条件的前提下，搜索第i＋1 行的每个位置填写什么数字。在到达搜索边界时(M个位置都填完)，就得到了一个状态k，从而可以从F[i,j]转移到F[i +1,k]。总而言之，整个动态规划算法使用三进制压缩的状态表示，以“行号”为阶段，在相邻两行之间使用DFS进行转移

#include<bits/stdc++.h>
using namespace std;
const int N=105,M=60000;
int n,m,ans,three[15]={1},f[N][M],s[15],p[15];
char g[N][12];
void toThree(int x){//10进制  转  3进制
	for(int i=0;i<m;i++)s[i]=x%3,x/=3;
} 
int toTen(int* a){//3进制  转  10进制 
	int x=0;
	for(int i=0;i<m;i++)x+=a[i]*three[i];
	return x;
}
void dfs(int i,int j,int cnt){
	int t=toTen(p);
	f[i][t]=max(f[i][t],cnt);
	ans=max(ans,f[i][t]);
	if(j>=m)return;
	for(int x=j;x<m;x++){
		if(p[x]==0&&s[x]==0&&g[i][x]!='H'){
			p[x]=2;
			dfs(i,x+3,cnt+1);
			p[x]=0;
		}
	}
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++)three[i]=three[i-1]*3;
	for(int i=1;i<=n;i++)scanf("%s",g[i]);
	memset(f,0x9f,sizeof(f));
	f[0][0]=0;
	for(int i=0;i<n;i++){//枚举行 
		for(int si=0;si<three[m];si++){//枚举第i行的状态 
			if(f[i][si]<0)continue;
			toThree(si);
			for(int j=0;j<m;j++)p[j]=max(0,s[j]-1); 
			dfs(i+1,0,f[i][si]);
		}
	}
	printf("%d",ans);
	return 0;
} 

例5：Mondriaan’s Dream

【题目描述】U204941蒙德里安的梦想
求把 N×M 的棋盘分割成若干个 1×2 的的长方形，有多少种方案。
例如：当 N=2，M=4时，共有 5 种方案。当 N=2，M=3 时，共有 3 种方案。 如下图所示：

【输入描述】
输入包含多组测试用例。
每组测试用例占一行，包含两个整数 N 和 M。 当输入用例 N=0，M=0 时，表示输入终止，且该用例无需处理。
【输出描述】
每个测试用例输出一个结果，每个结果占一行。

【解法1】《算法竞赛进阶指南》P303
若n和m都是奇数方案为0，根据面积的奇偶性可以证明（不加该优化也可AC），
假设n≥m，对于某种已经铺满的方案，以行为单位，将棋盘分割为两半，在上半部分的最后一行中：

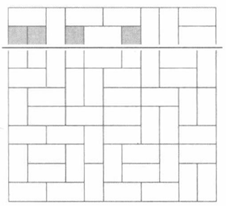
（1）每个灰色背景的部分都是一个竖着的1×2长方形的一半，决定了下一行必须继续补全该长方形。
（2）其余部分对下半部分的分割方法没有影响。下一行既可以在连续两个位置安排一个横着的1*2长方形,也可以让某个位置作为一个竖着的1×2长方形的一半。

综上所述，我们可以把“行号”作为DP的“阶段”，把“上半部分”不断向下扩展，直至确定整个棋盘的分割方法。为了描述上半部分最后一行的详细形态，我们可以使用一个M位二进制数,其中第k(0≤k<M)位为1表示第k列是一个竖着的1×2长方形的上面一半，第k位为0表示其他情况。

• 状态设计：设 $f[i,j]$表示第i行的形态为j 时，前i行分割方案的总数。j是用十进制整数记录的M位二进制数。
• 状态转移：第i-1行的形态k能转移到第i行的形态j，当且仅当:
  （1）j和k执行按位与运算的结果是0。这保证了每个数字1的下方必须是数字0，代表继续补全竖着的1×2长方形。
  （2）j和k 执行按位或运算的结果的二进制表示中，每一段连续的0都必须有偶数个。
• 预处理：在DP前预处理出$[0,2^M?1]$内所有满足“二进制表示下每一段连续的0都有偶数个”的整数,记录在集合S中。
• 转移方程：$f[i,j]=\sum f[i?1,k]$，其中j&k=0且j|k∈S
• 初始状态：$f[0][0]=1$,其余均为0
• 目标状态：$f[n][0]$

#include<bits/stdc++.h>
using namespace std;
const int N=15;
long long n,m,can[1<<12],f[N][1<<12];

int main(){
	
	while(scanf("%lld%lld",&n,&m)&&n){
		memset(f,0,sizeof(f));
		memset(can,0,sizeof(can));//状态连续0的个数必须是偶数个 
		for(int i=0,ms=1<<m;i<ms;i++){
			int yes=1,one=0;
			for(int j=0;j<m;j++){
				if(i&(1<<j))yes&=(one%2==0),one=0;
				else one++;
			}
			yes&=(one%2==0);
			can[i]=yes;
		} 
		f[0][0]=1;
		for(int i=1;i<=n;i++)
			for(int j=0;j<(1<<m);j++)
				for(int k=0;k<(1<<m);k++)
					if((j&k)==0&&can[j|k])
						f[i][j]+=f[i-1][k];
		printf("%lld\n",f[n][0]);
	}
	return 0;
} 

【解法2】

• 本题也可以采用3进制压缩状态，按解法1中的方式分割后每列只有三种情况：
  0——“横放的完整块”
  1——“竖着的上半部分”
  2——“竖着的下半部分”
• 若压缩的状态中含有0，则必须有连续的偶数个，可预处理出所有合理的状态（约14000个）
• 状态定义：$f[i][S_i]$表示第i行的放置状态为$S_i$时，铺满前i行的方案数。
• 状态转移：若$S_i$的第j个位置上为0或2，则$S_{i+1}$的第j个位置上可以填0或1；若$S_i$的第j个位置上为1，则$S_{i+1}$的第j个位置上只能填2；填写过程中需要满足连续0的个数为偶数个。
• 实现方式：dfs填数，并根据连续0的情况判断是否剪枝。
• 边界条件：$f[1][x]=1$，状态x的三进制中不含有2
• 答案统计：$ans+=f[n][x]$，状态x的三进制中不含有1

#include<bits/stdc++.h>
using namespace std;
const int N=15,M=2e5;
int n,m,three[15]={1},p[15],np[15];
long long ans,f[N][M];
int toTen(int* x){//转换为10进制 
	int y=0;
	for(int i=0;i<m;i++)y=y+x[i]*three[i];
	return y;
}
void toThree(int x){for(int i=0;i<m;i++)p[i]=x%3,x/=3;}
bool check(int x){//检查状态x中的0是否连续偶数个 
	toThree(x);
	int y=1,z=0;
	for(int i=0;i<m;i++)
		if(p[i]==0)z++;
		else y&=(z%2==0),z=0;
	return y&(z%2==0);
}
bool has(int x){//检测状态中是否含有数字x 
	for(int i=0;i<m;i++)
		if(p[i]==x)return 1;
	return 0;
}
void dfs(int i,int j,int zero,int x){//从状态x转移，填到第i行第j列时连续0的个数 
	if(j==m){
		if(zero%2==0)f[i][toTen(np)]+=f[i-1][x];
		return;
	}
	if(p[j]%2==0){//0,2下方可填0,1 
		np[j]=0,dfs(i,j+1,zero+1,x); 
		if(zero%2==0)np[j]=1,dfs(i,j+1,0,x);
	}
	else{
		if(zero%2==0)np[j]=2,dfs(i,j+1,0,x);
	}
}
int main(){
	for(int i=1;i<=11;i++)three[i]=three[i-1]*3;
	while(scanf("%d%d",&n,&m)&&n){
		ans=0;
		if(n<m)swap(n,m); 
	    if(n%2==0||m%2==0){
			memset(f,0,sizeof(f));
			for(int x=0;x<three[m];x++)
				if(check(x)&&!has(2))
					f[1][x]=1;
			for(int i=1;i<n;i++)
				for(int j=0;j<three[m];j++)
					if(f[i][j]>0){
						toThree(j);
						dfs(i+1,0,0,j);
					}
			for(int j=0;j<three[m];j++)
				if(f[n][j]>0){
					toThree(j);
					if(!has(1))ans+=f[n][j];
				}	
		}
		printf("%lld\n",ans);
	}
	return 0;
} 

二、集合类状态压缩DP

例6：最优点集配对问题

【题目描述】UVA10911
二维平面上有n个点$P_0,P_1,\dots \dots ,P_{n?1}$,你的任务是把他们配成n/2对（n是偶数），使得每个点恰好在一个点对中。所有点对中两点的距离之和应尽量小。
【输入描述】
输入第一行为一个整数n，
接下来n行，每行2个整数x y表示坐标
【输出描述】
输出最小距离之和
【数据范围】
n≤20,|x|,|y|≤10000.

这个任务必然是一步一步的完成：先给$P_0$配对，然后$P_1$配对……，每一步都可以看做是完成这个任务的一个阶段（配对的对数为阶段）
按照序列问题定义状态：d(i)表示前i个点两两配对的最小距离和。
状态转移：考虑第i个点的决策——和谁配对？
假设i和j配对，问题转换为“将前i-1个点中除了j以外的其他点两两配对”
显然，光一个d值无法搞定“除了j以外的其他点”这个条件的
因此，给状态增加维度，前i个点是一个集合，除j以外，就是在集合中减去j；因此增加维度 “集合”

• 状态定义：d(i,s)表示前i个点中位于集合s中的元素两两配对的最小距离和。
• 状态转移方程：$d(i,s)=min|P_i{P}_j|+d(i?1,s?i?j)，其中j\in s，|P_i{P}_j|表示i，j之间的直接距离$

【优化】
上述状态定义中i其实可以不要，因为i其实就是s中最大的那个点

• 状态定义：d(s)表示点集s中的元素两两配对的最小距离和
• 状态转移方程： $d(s)=min|P_i{P}_j|+d(s?i?j)，其中i是s中最大的那个点,j\in s$

#include<bits/stdc++.h>
using namespace std;
const int N=18,inf=1e9;
double x[N],y[N],dis[N][N],dp[1<<N];
double getDis(int i,int j){
	double xx=x[i]-x[j],yy=y[i]-y[j];
	return sqrt(xx*xx+yy*yy);
}
int calOne(int s){
	int t=0;
	while(s)t++,s-=(s&(-s));
	return t;
}
int main(){
	int t=0,n,maxs;
	char name[30];
	while(scanf("%d",&n)&&n){
		n*=2,maxs=1<<n,dp[0]=0;
		for(int i=0;i<n;i++)
			scanf("%s%lf%lf",name,&x[i],&y[i]);
		for(int i=0;i<n;i++)
			for(int j=i+1;j<n;j++)
				dis[i][j]=dis[j][i]=getDis(i,j);
		for(int s=1;s<maxs;s++){
			int i,j;
			dp[s]=inf;
			if(calOne(s)%2)continue;//奇数个点，必然配对不成功
			for(i=n-1;i>=0;i--)//找到s中最大的点i 
				if(s&(1<<i))break;
			for(int j=i-1;j>=0;j--)//找到s中可以和i点配对的点 
				if(s&(1<<j))dp[s]=min(dp[s],dis[i][j]+dp[s^(1<<i)^(1<<j)]);
		}
		printf("Case %d: %.2lf\n",++t,dp[maxs-1]);
	}
	return 0;
}

例7：TSP_旅行商问题

【题目描述】
某乡有n个村庄(1<n≤20)，有一个售货员，他要到各个村庄去售货，各村庄之间的路程s(0<s<1000)是已知的，且A村到B村与B村到A村的路大多不同。为了提高效率，他从商店出发到每个村庄一次，然后返回商店所在的村，假设商店所在的村庄为1，他不知道选择什么样的路线才能使所走的路程最短。请你帮他选择一条最短的路。
【输入格式】
村庄数n和各村之间的路程(均是整数)。
【输出格式】
最短的路程。
【输入样例】
3
0 2 1
1 0 2
2 1 0
【输出样例】
3

为了与进制压缩保持一致，将节点从0开始编号，并且0号点就是商店；

• 状态定义：$f(i,s)$表示访问完集合 s 中各点一次后停在城市 i 的最短路长度。
• 状态转移：假设从j出发到达i，则问题转换为停在j点时访问集合中除i以外的城市各一次的最短路长度；
• 转移方程：$f(i,s)=minf(j,s?i)+dis(j,i)，其中j\in s$
• 边界条件：$f(0,1)=0$
• 答案：$min(f(x,2^n?1)+dis[x][0]);其中x\in [0,n?1]$
• 时间复杂度：$O(n^2?2^n)$

#include<bits/stdc++.h>
using namespace std;
const int N=20;
int n,maxs,ans,dis[N][N],dp[N][1<<N];//在i点且状态构成的集合为s时的最短路 
int main(){
	scanf("%d",&n);
	memset(dp,0x3f,sizeof(dp)); 
	maxs=(1<<n),ans=dp[0][0];
	for(int i=0;i<n;i++)
		for(int j=0;j<n;j++)
			scanf("%d",&dis[i][j]);
	dp[0][1]=0;
	for(int s=1;s<maxs;s+=2)
		for(int i=0;i<n;i++){
			if((s&(1<<i))==0)continue;//点集中不存在i点 
			for(int j=0;j<n;j++)//从j走到i 
				if(i!=j&&(s&(1<<j)))
					dp[i][s]=min(dp[i][s],dp[j][s^(1<<i)]+dis[j][i]);
		}
	for(int i=1;i<n;i++)ans=min(ans,dp[i][maxs-1]+dis[i][0]);
	printf("%d\n",ans);
	return 0;
} 

例8：Hie with the Pie

【题目描述】POJ3311
有一个人从0点出发送披萨到n（n≤10）个点并且最后要回到0点，每个点可以重复多次经过，题目给出任意两点i,j直达需要花的时间，但是可能i到j的直达时间不如i经过其他点后到j小；求送n份披萨并回到0点的最少时间
【输入描述】
输入包含多组输入，每组输入第一行为整数n，n=0则结束
接下来n+1行，每行n+1个整数;第i行的第j个数表示点i-1到j-1的直达时间
【输出描述】
每组数据输出送n份披萨并回到0点的最少时间

• 预处理：采用Floyd求出任意两点间的最短路，Floyd能使用的前提是每个点可多次经过。
  任意点对间的最短路已知，接下来只需要确定送披萨的顺序即可
• 方案1：生成1~n的全排列，按照排列顺序送，每种排列下求出路径长度，取最小值即可。时间复杂度为O(n*n!)，全排列可通过next_permutation函数或DFS生成。
• 方案2 ：对解法1进行优化，采用DFS生成全排列，生成过程中计算路径长度，并且可最优化剪枝（当前路径已经比已有的最优解大），时间复杂度O(n!)
• 方案3：N的规模为14，应该有两个反应——搜索或状压；
  预处理出任意两点的距离后，接下来就是每个点访问一次——TSP
  状态设计：$f[i][s]$ 表示访问完集合s中的所有点，并且最后停在i点需要的最少时间。
  转移方程： $f[i][s]=min(f[j][s?i]+dis[j][i])$;
  边界条件：$f[0][1]=0$，其他的都是无穷大;//i点为第一个达到的点时时间为dis[0][i]
  答案：$ans=min(ans,f[i][(1<<(n+1))?1]+dis[i][0])$; //不光要都去过，且要回去

例9：Travelling

【题目描述】U205514
Mr ACMer想要进行一次旅行，他决定访问n（n≤10）座城市。Mr ACMer可以从任意城市出发，必须访问所有的城市至少一次，并且任何一个城市访问的次数不能超过2次。n座城市间有m条道路，每条道路都有一个费用。求Mr ACMer 完成旅行需要花费的最小费用。如果不能完成旅行，则输出-1。
【输入描述】
输入包含多组输入，每组输入第一行为两个整数n m，
接下来m行，每行三个整数a b c表示a与b之间有一道路费用为c
【输出描述】
每组数据输出最小花费或-1

注意：这里不能用floyd预处理，任意点对间的最短路，因为每个点经过的次数上限。
压缩：因为每个城市被访问的次数只可能是0,1,2，因此采用三进制压缩。
状态设计：设$f[i][s]$表示各个点访问状态为s，且最后停在i点时的最小花费
转移分析：若最后从j走到i导致i点经过次数加1，并且最后得到了状态s，则在j点时的状态为$s’=s?3^i$。
状态转移：$dp[i][s]=min(dp[j][s?3^i]+dis[j][i])$;
边界条件：$dp[i][3^i]=0$ //从任意城市出发，则从i出发是i的次数为1，其他地方都为0
目标状态：$dp[i][s]$，其中s不得包含0

#include <bits/stdc++.h>
using namespace std;
const int N=11,M=60000,inf=0x3f3f3f3f;
int n,m,dis[N][N],dp[N][M],three[N]={1},sta[M][N];
void init(){
    for(int i=1; i<N; i++)three[i]=three[i-1]*3;
    for(int i=0; i<three[N-1]; i++)
        for(int j=0,t=i; j<N; j++)
    		sta[i][j]=t%3,t/=3;
}
bool hasZero(int i){
	for(int j=0;j<n;j++)
		if(sta[i][j]==0)return 1;
	return 0;
}
int main()
{
    init();
    while(~scanf("%d%d",&n,&m))
    {
        memset(dis,0x3f,sizeof(dis));
        memset(dp,0x3f,sizeof(dp));
        for(int i=0,a,b,c;i<m;i++){
            scanf("%d%d%d",&a,&b,&c);
            a--,b--;
            dis[a][b]=dis[b][a]=min(c,dis[a][b]);
        }
        for(int i=0;i<n; i++)dp[i][three[i]]=0;//dp边界
        for(int s=0; s<three[n]; s++)
			for(int i=0;i<n;i++)
        		if(sta[s][i])
					for(int j=0;j<n;j++)
						if(sta[s][j])
							dp[i][s]=min(dp[i][s],dp[j][s-three[i]]+dis[j][i]);
		int ans=inf;		
		for(int s=0; s<three[n]; s++)
			if(!hasZero(s))
				for(int i=0;i<n;i++)
					ans=min(ans,dp[i][s]);
        printf("%d\n",ans>=inf?-1:ans);
    }
    return 0;
}