[数据结构与算法]必须使用的硬币（从后往前递推、枚举缺少这枚硬币的情况）bitset+二进制优化多重背包

4120:硬币

分别存放 从前往后、从后往前的地推结果，枚举缺少第 i 枚硬币的情况

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int N=205;
int w[N];
int dp[N][10005]; 
int dp2[N][10005]; 
int main(){
	int n,x;
	cin>>n>>x;
	for(int i=1;i<=n;i++){
		cin>>w[i];//面值 
	}
//	fill(dp,dp+n+1,0xc0c0c0c0);
//虽然是恰好装满型，但不求最大价值，只求能否装满，于是dp数组只有
//0，1两种值 
//	fill(dp,dp+n+1,0);
	dp[0][0]=1;
	for(int i=1;i<=n;i++){
		for(int j=0;j<=x;j++){
//			dp[i][j]=dp[i-1][j]||dp[i-1][j-w[i]];
			dp[i][j]=dp[i-1][j];//不取第i个硬币 
			if(j>=w[i])dp[i][j]|=dp[i-1][j-w[i]]; 
		}
	}
	dp2[n+1][0]=1;//第n+1个硬币不存在，取的自然为0，状态可
//	dp2[i][j]表示第i~n个硬币中是否能取到总和j 
	for(int i=n;i>=1;i--){
		for(int j=0;j<=x;j++){
//			dp2[i][j]=dp2[i+1][j]||dp2[i+1][j-w[i]];
			dp2[i][j]=dp2[i+1][j];
			if(j>=w[i])dp2[i][j]|=dp2[i+1][j-w[i]]; 
		}
	} 
	vector<int> res;
	for(int i=1;i<=n;i++){//枚举缺少每个硬币 
		int flag=1;
		for(int j=0;j<=x&&flag;j++){
			if(dp[i-1][j]&&dp2[i+1][x-j]){
//				res.push_back(w[i]);
//				break;莫疯了，但凡能拼出x的组合，i就是非必要 
				flag=0;
			}
		} 
		if(flag)res.push_back(w[i]);
	} 
	int cnt=res.size();
	cout<<cnt<<endl;
	sort(res.begin(),res.end());
	for(int i=0;i<cnt;i++)cout<<res[i]<<" ";
    return 0;
}

中途犯了一个错误：

	dp[0][0]=1;
	for(int i=1;i<=n;i++){
		for(int j=w[i];j<=x;j++){
			dp[i][j]=dp[i-1][j]||dp[i-1][j-w[i]];
		}
	}

大概只要清醒就能发现显而易见的错误，
二维dp数组却$j$却从$w[i]$枚举

决定统一成这样的形式

	dp[0][0]=1;
	for(int i=1;i<=n;i++){
		for(int j=0;j<=x;j++){
//			dp[i][j]=dp[i-1][j]||dp[i-1][j-w[i]];
			dp[i][j]=dp[i-1][j];//不取第i个硬币 
			if(j>=w[i])dp[i][j]|=dp[i-1][j-w[i]]; 
		}
	}

统一成这样的形式的好处，
分组背包（多重背包），第i组 至少要取一个（hdu4968 最大最小GPA）
在枚举第i组的s种决策之前， 就不可 dp[i][j]=dp[i-1][j];
因为这代表第s+1种决策，在第i组不取，延续在前i-1组取到的值
if(j>=k*w[i])dp[i][j]=max(dp[i][j],dp[i-1][j-k*w[i]]+k*v[i]);
也就是，到底 在第i组是否必须取（第i种物品是否必须取）
至于这里 ，大抵是忘记了，0-1背包二维最初写法，还有
二维写法，j永远是从0开始枚举的，压成一维才要从w[i] ,而且还有 else dp[i][j]=dp[i-1][j];

解法二：ans数组表示不取第i枚硬币取得总和j的取法

对于解法二可能理解的还是不够透彻，因为我不能把滚动数组还原成二维数组
之后再试试

#include<iostream>
#include<stdio.h>
#include <stdlib.h>
#include <math.h>
#include<algorithm>
//#include <bits/stdc++.h>
using namespace std;
int a[205];
int dp[10005];//对于前i种货币取得总金额j的取法 
int ans[10005];//不取第i种取得金额j的取法 
int res[205];
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	int n,k;
	cin>>n>>k;
	for(int i=1;i<=n;i++){
		cin>>a[i];
//		dp[i][a[i]]=1; 
//		dp[i][0]=1;
	}
	//先求出dp数组，ans[i][k]==0则第i个是必须的 
	dp[0]=1;
	for(int i=1;i<=n;i++){
		for(int j=k;j>=a[i];j--){
			dp[j]=dp[j]+dp[j-a[i]];
		}
	} 
	int cnt=0;
	ans[0]=1;
	for(int i=1;i<=n;i++){
		for(int j=0;j<=k;j++){
			if(j<a[i]){
				ans[j]=dp[j];
			}
			else{//j==a[i]时 ans[0]表示取a[i]来获取j的情况
//			也就是 不取a[i]获得0的情况，只有一种，初始化为0了 
				ans[j]=dp[j]-ans[j-a[i]];
//				dp[i][j]=dp[i-1][j]+dp[i-1][j-a[i]]; 
				//获取j的方法 -取a[i]来获得j的方法 
//				但这里注意是减去ans[j-a[i]]，虽然而不是dp[j-a[i]]
//				因为不是dp[i-1][j-a[i]]，而是dp[i][j-a[i]] 
 //这里理解有点困难，dp[j]表示可以包括a[i]也可以不包括a[i]，凑成j面值的方法数，
 //ans[j-a[i]]表示不带a[i]可以凑成                                                  
// j-a[i] 的方法总数， j - a[i] + a[i]就是j，也就是ans[j - a[i]]是
//必须带上a[i]能凑成j 面值的方法总数，两者减就是不带上a[i] 凑成 j面值的方法数
			}
		}
		if(ans[k]==0){
			res[cnt++]=a[i];
		}
	}
	cout<<cnt<<endl;
	if(cnt){
			cout<<res[0];
	for(int i=1;i<cnt;i++){
		cout<<" "<<res[i];
	}
	}
	else cout<<endl;
    return 0;
}
//	dp[i][j]=max(dp[i-1][j],dp[i-1][j-a[i]]);不总是取max而是相加 

对于每一种和为m的选择方案，如果其中有一个硬币面值a[i]可以由其他面值的硬币表示出来，那么它就不是必须选择的硬币，即如果从所有硬币中去掉a[i]面值的硬币，dp[m]的值变成0，也就是没有方案能凑成m，那么a[i]就是不能缺少的硬币。
思路来源
介绍容斥原理
递归求解

必带的时光胶囊（多重背包）

https://ac.nowcoder.com/acm/contest/4912

#include<iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N=1e5+5;
bool dp1[500][N];
bool dp2[500][N];
int w[N];
int cnt[N];

int main() {
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>w[i];
		cnt[w[i]]++;
	}
//	1、当作0-1背包，相同质量的胶囊看作两个不同的胶囊，TLE
//	2、多重背包，搞三重循环，同上，肯定超时
//	3、对多重背包进行二进制优化
//	4、对多重背包进行二进制+bitset优化 
	sort(w+1,w+n+1);
	n=unique(w+1,w+n+1)-(w+1);//去重 
	
	dp1[0][0]=1;
	for(int i=1;i<=n;i++){
		for(int j=0;j<=m;j++){
			dp1[i][j]=dp1[i-1][j];//不取第i种
			int t=cnt[w[i]];
			for(int k=1;k<=t;k++){
				if(j>=k*w[i])dp1[i][j]+=dp1[i-1][j-k*w[i]];
			} 
		} 
	} 
	dp2[n+1][0]=1;
	for(int i=n;i>=1;i--){
	for(int j=0;j<=m;j++){
		dp2[i][j]=dp2[i+1][j];//不取第i种
		int t=cnt[w[i]];
		for(int k=1;k<=t;k++){
			if(j>=k*w[i])dp2[i][j]+=dp2[i+1][j-k*w[i]];
		} 
	} 
} 
	vector<int> v;
	for(int i=1;i<=n;i++){
		int flag=1;//假设第i种是必要的
		 for(int j=0;j<=m&&flag;j++){
		 	if(dp1[i-1][j]&&dp2[i+1][m-j])flag=0;
		 } 
		 if(flag)v.push_back(w[i]);
	}
	int s=v.size();
	cout<<s<<endl;
	sort(v.begin(),v.end());
	for(int i=0;i<s;i++){
		cout<<v[i]<<" ";
	}
    return 0;
}

wa1：
报错一大堆还提示多次包含dp2这个关键字，以为重名了，其实不然，数组开得大的离谱

const int N=1e5+5;
int dp1[N][N];
int dp2[N][N];

这么大的数组以后别再开了

wa2：
改成int dp[455][N];后，内存超时
上面那个空间超限是碾压式的无法挽救的，但这个可以
dp值只有0、1两种状态的dp数组，建议用bool dp[N][N]
平时数据小看不出，到了一定程度，bool还是比int节省空间的

wa3：段错误，找半天，没输入m
wa4：意料的超时

想超个时都不那么顺利TT

不同物品总数不超过M，物品种数最多$sqrt(M)$!!!

有一个特别优美的性质就是不同类的物品总大小不超过 $10^5$，这说明了最多只有 $\sqrt{10^5}\approx 450$种物品（$1+2+3+?+n\approx n^2）$

二进制+bitset优化

#include<iostream>
#include <algorithm>
#include <vector>
#include <bitset>
using namespace std;
const int N=1e5+5;
//bool dp1[500][N];
//bool dp2[500][N];
int w[N];
int cnt[N];
bitset<N>dp1[455];
bitset<N>dp2[455];
int main() {
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>w[i];
		cnt[w[i]]++;
	}
//	1、当作0-1背包，相同质量的胶囊看作两个不同的胶囊，TLE
//	2、多重背包，搞三重循环，同上，肯定超时
//	3、对多重背包进行二进制优化
//	4、对多重背包进行二进制+bitset优化 
	sort(w+1,w+n+1);
	n=unique(w+1,w+n+1)-(w+1);//去重 
	
	dp1[0][0]=1;//第0种物品取0的情况啦
//	 第0种物品对应的(bitset<N>) dp[0] ,0000……0001 
//二进制+bitset 
	for(int i=1;i<=n;i++){
		int t=cnt[w[i]];//第i组有t个
		int x=w[i]; 
//		用bitset枚举从t个种选若干个的决策（长t序列的子集） 
		dp1[i]=dp1[i-1];//不取，那么得到的所有和就是取前i-1组得到的 
		for(int k=1;k<=t;t-=k,k<<=1,x<<=1){ 
			dp1[i]|=(dp1[i]<<x); 
		} 
		dp1[i]|=(dp1[i]<<t*w[i]);
	} 
	dp2[n+1][0]=1;
	for(int i=n;i>=1;i--){
		int t=cnt[w[i]];
		int x=w[i];
		dp2[i]=dp2[i+1];
		for(int k=1;k<=t;t-=k,k<<=1,x<<=1) {
			dp2[i]|=(dp2[i]<<x);
		}
		dp2[i]|=(dp2[i]<<t*w[i]);
} 
	vector<int> v;
	for(int i=1;i<=n;i++){
		int flag=1;//假设第i种是必要的
		 for(int j=0;j<=m&&flag;j++){
		 	if(dp1[i-1][j]&&dp2[i+1][m-j])flag=0;
		 } 
		 if(flag)v.push_back(w[i]);
	}
	int s=v.size();
	cout<<s<<endl;
	sort(v.begin(),v.end());
	for(int i=0;i<s;i++){
		cout<<v[i]<<" ";
	}
    return 0;
}

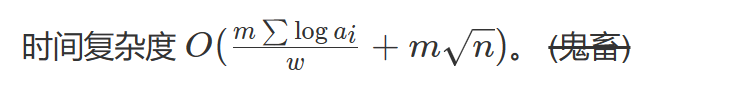
其实就是二进制解决多重背包，化成0
本来单单二进制优化多重背包是将多重背包优化成0-1背包，再递推来做。
但这里，因为要得到某一组种所有物品的选取决策，相当于枚举所有的子集了，但简单枚举二重循环也免不了超时，所以要把内层循环（枚举所有子集的）的复杂度从 $n??>lo{g}_{2}n$,才能勉强卡进1s
枚举所有的子集，本来是每加入一个元素，在上次得到的所有结果的基础上再加上该元素，产生了新的一些和。
但这里，只需要，每加入 前1个， 前2个， 前4个， 前$2^{?}$个，把该序列的长度由$n$变为$lo{g}_{2}n$，t个元素能组合成的和，都能通过这$lo{g}_{2}n$个数组合而成，同时注意加入时是打包的值。