1.二叉树的顺序存储

1.1存储方式

完全二叉树/满二叉树建议使用顺序表存储因为没有空间的浪费，不用存储空节点，其他二叉树不建议用顺序表存储（数组）
将二叉树用层序遍历方式放入数组中，这种方式的主要用法就是堆的表示。
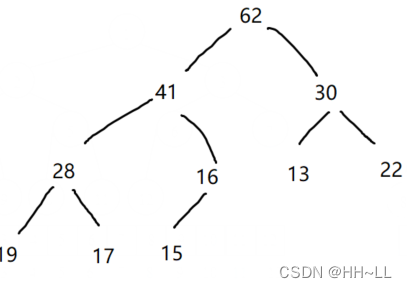
在这里插入图片描述
层序遍历结果

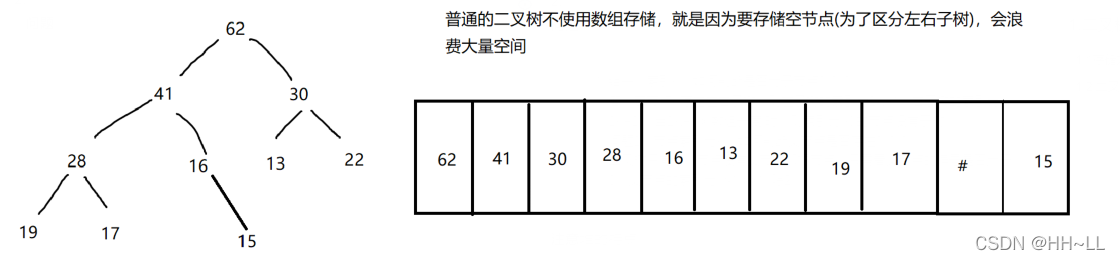
1.2 二叉树的节点编号关系

已知父节点(parent)的下标，则：左孩子(left)下标 = 2 * parent + 1;右孩子(right)下标 = 2 * parent + 2;
已知孩子（不区分左右）(child)下标，则：双亲(parent)下标 = (child - 1) / 2;
问题

给一个索引K，如何判断是否为子节点？？？
答：若节点K存在左右子树，则左子树的索引为2K+1，右子树的索引为2K+2 ；当2K+1 > 数组长度时，则索引为 K 的节点没有子树
问题2：节点索引为K，如何判断父节点是否存在？？？
二叉树只有一个节点没有父节点即根节点，只需看父节点的编号是否大于0，父节点的索引为(k-1)>>1;(除2)

2.堆概念

2.1 概念

堆逻辑上是一棵完全二叉树
堆物理上是保存在数组中
堆中根节点值>=子树中的节点值，叫做大堆，或者大根堆，或者最大堆
堆中根节点值<=子树节点值，则是小堆，或者小根堆，或者最小堆
堆的基本作用是，快速找集合中的最值

最大堆，节点所在的层次越高，节点值越大是错误的只能保证当前根节点>=子树中所有节点，任意子树中仍然满足这个特点，节点的大小关系与层次无关
例如：

2.2 堆的一些基本操作

2.2.1 简单操作

// 判断堆是否为空
    public boolean isEmpty() {
        return data.size() == 0;
    }
    // 根据索引得到父节点的索引
    private int parent(int k) {
        return (k - 1) >> 1; // (k-1)/2
    }
    // 根索引得到左子树的索引  (k<<1)+1
    private int leftChild(int k) {
        return (k << 1) + 1; //2k+1
    }
    // 根索引得到右子树的索引  (k<<1)+2
    private int righttChild(int k) {
        return (k << 1) + 2;  // 2k+2
    }

2.2.2 向最大堆中添加一个新元素

两个步骤：

步骤1. 直接在数组末尾新增元素->结构上保证添加元素之后，这颗二叉树还是完全二叉树
步骤2. 添加新元素后，调整新元素的位置，使得这棵完全二叉树仍然满足最大堆的性质

步骤1：首先数组末尾新增元素
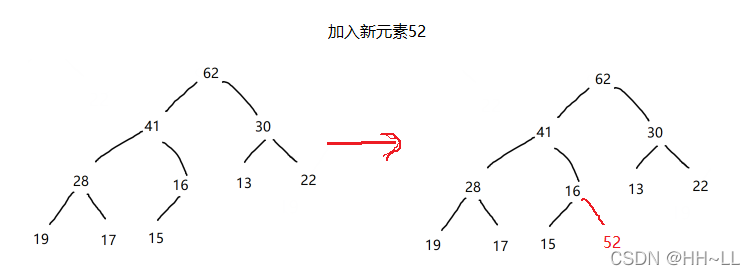
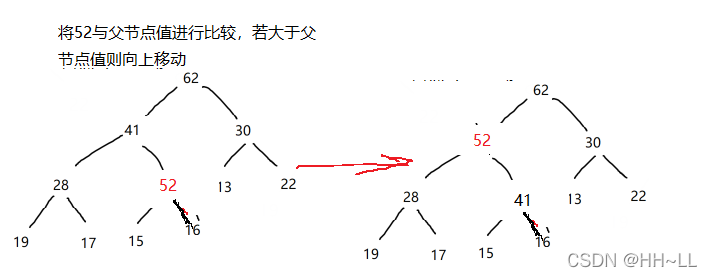
在这里插入图片描述
步骤2：要使增加元素后的堆满足最大堆的特点，则需要将新增的元素52进行上浮操作。将当前节点与父节点进行比较，若大于父节点则交换

元素上浮的两个终止条件
1.当前节点值<=父节点值（已处于最终位置）
2.已经走到根节点

在这里插入图片描述

package bin_tree.heap;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.NoSuchElementException;
public class MaxHeap {
    // 使用JDK的动态数组ArrayList存储最大堆
    List<Integer> data;
    public MaxHeap() {
        // 构造方法的this调用
        this(10);
    }
    // 初始化堆操作
    public MaxHeap(int size) {
        data = new ArrayList<>(size);
    }
    // 向最大堆中添加新元素val
    public void add(int val) {
        // 1.直接在数组末尾添加元素
        data.add(val);
        // 2.进行元素得上浮操作
        sifUp(data.size() - 1);
    }

    public void sifUp(int k) {
        // 上浮操作得终止条件: 已经走到根节点|| 当前节点值<=父节点值
        // 循环的迭代条件：还存在父节点 && 当前节点值>父节点值
        while (k > 0 && data.get(k) > data.get(parent(k))) {
            swap(k, parent(k));
            k = parent(k);
        }

    }
    private void swap(int i, int j) {
        int tmp = data.get(i);
        data.set(i, data.get(j));
        data.set(j, tmp);
    }
    }