[数据结构与算法]Leetcode--Java--430. 扁平化多级双向链表

题目描述

样例描述

思路

方法一：递归 + 迭代 O(n^2)

1. 没孩子结点就一直next，如果有孩子结点，就先存储当前结点的下一个，然后不断递归（将孩子部分先展平），随后拼接当前结点和展平后的部分，并将当前结点的孩子指针设置为null，然后寻找展平部分的最后一个结点与原始当前结点的下一个结点进行拼接。 最后将当前结点设置为原始的下一个，准备下一轮迭代。

方法二：对方法一的优化：额外写递归函数 O(n)

1. 方法一中由于每次是从head.child开始递归，又要每一次再次遍历寻找展平部分的尾结点。这里最坏情况复杂度是平方。
2. 单独写递归函数，每次直接返回展平后的"尾结点"，使得找尾结点的部分不会在每一层出现，可以达到O(n)
   递归拼接顺序如下：
   

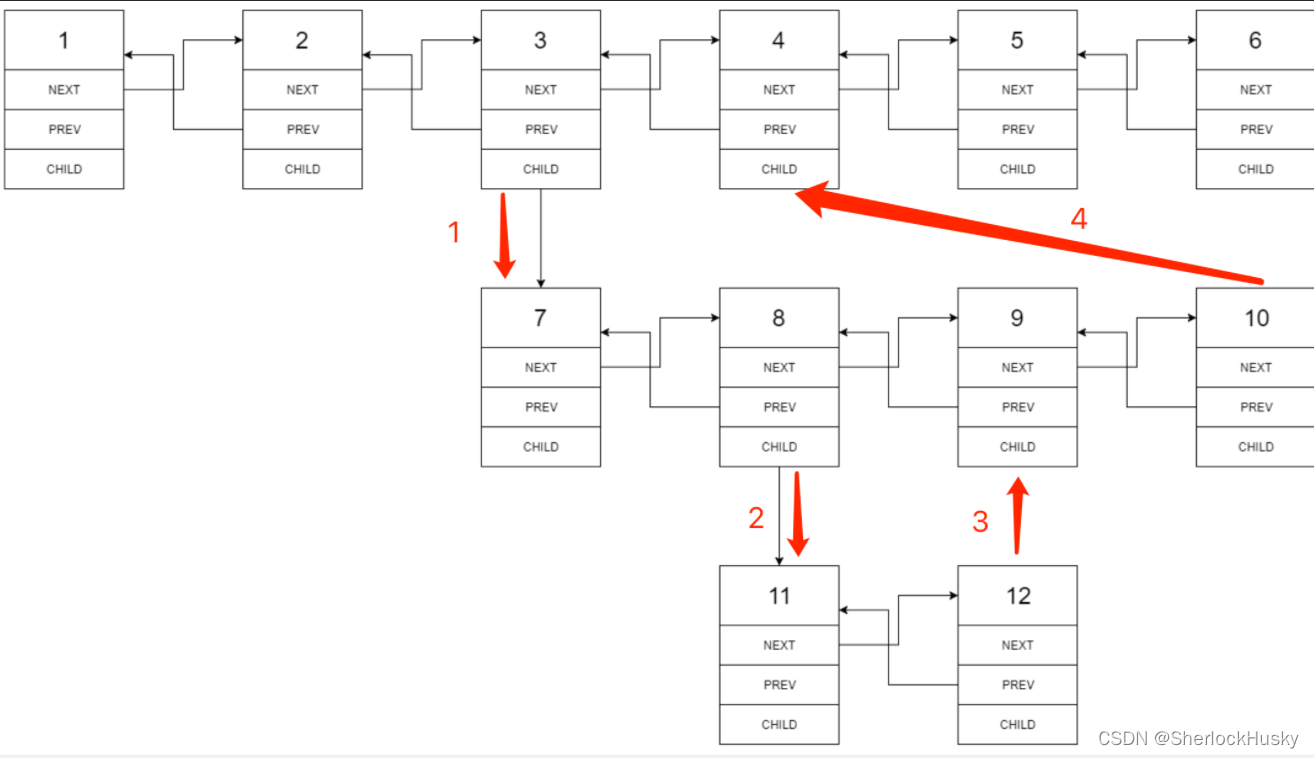
方法三： 迭代
迭代的拼接顺序与递归不同，是一段一段进行的，区别如下：

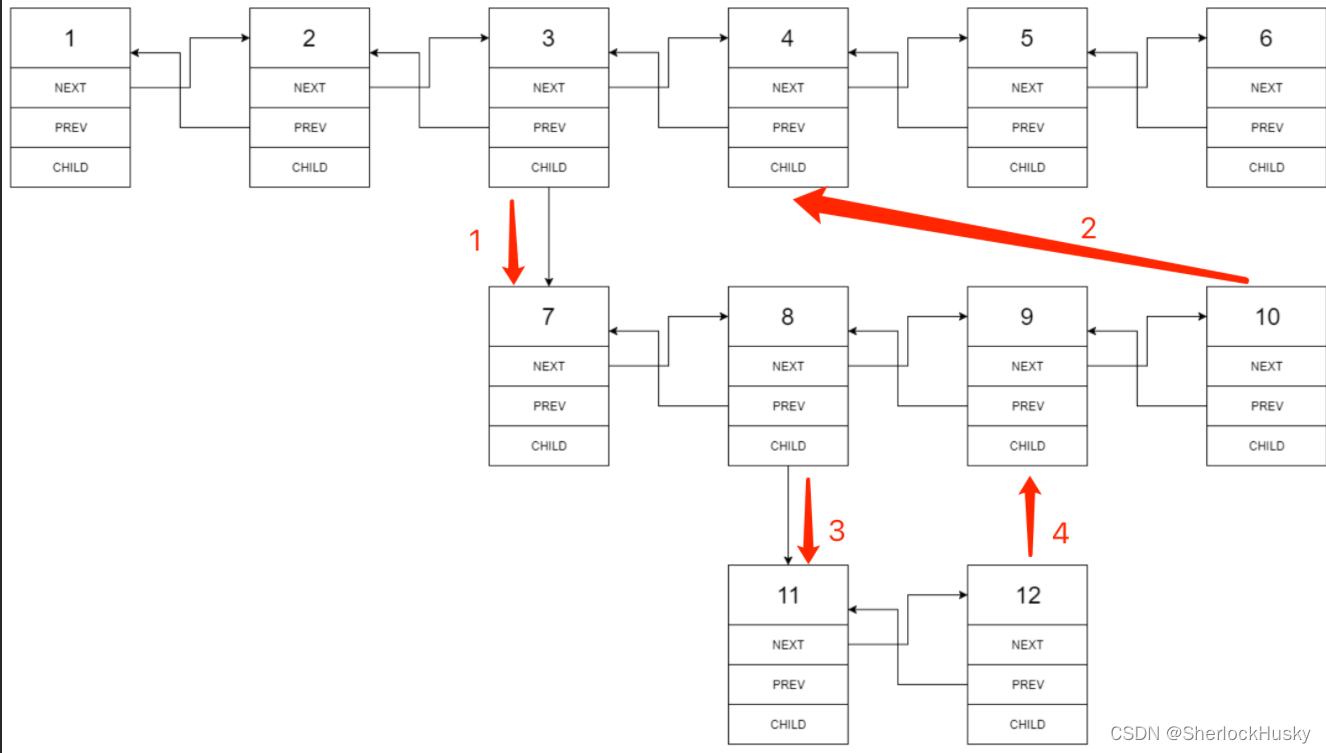
1. 让head从最开始一直走，只要child不为空，就先迭代拼接处理完child层，然后继续往后，碰到有child就拼接。（虽然head会越遍历越长，因为不断拼接了child层，但是对每个结点只会访问常数次）

代码

方法一：

/*
// Definition for a Node.
class Node {
    public int val;
    public Node prev;
    public Node next;
    public Node child;
};
*/

class Solution {
    public Node flatten(Node head) {     
        Node dummy = new Node(-1);
        dummy.next = head;
        while (head != null) {
            if (head.child == null) {
                head = head.next;
            } else {
                //先存下当前的下一个结点
                Node nextN = head.next;
                //递归不断地展平，得到展平后的第一个结点
                Node flatnode = flatten(head.child);
                //将当前结点与展平后那块链表进行拼接
                head.next = flatnode;
                flatnode.prev = head;
                //这里要让孩子指针为null，因为上面已经展平
                head.child = null;
                //寻找展平后的最后一个结点，与原始head的下一个结点进行拼接 （也就是融入head所在层）
                while (head.next != null) {
                    head = head.next;
                }
                head.next = nextN;
                //这里一定要判断下是否为null，不然空会有异常
                if (nextN != null)
                nextN.prev = head;
                //然后让head更新为next，准备下一轮迭代
                head = nextN;
            }
        }
        return dummy.next;
    }
}

方法二：优化递归

/*
// Definition for a Node.
class Node {
    public int val;
    public Node prev;
    public Node next;
    public Node child;
};
*/

class Solution {
    public Node flatten(Node head) {
        dfs(head);
        return head;
    }
    //返回展平后的尾结点，返回给上一层使用
    public Node dfs(Node head) {
        Node last = head;
        while (head != null) {
            if (head.child == null) {
                last = head;
                head = head.next;
            } else {
                Node nextN = head.next;
                Node lastChild = dfs(head.child);
                //拼接head以及head的下一个
                head.next = head.child;
                head.child.prev = head;
                //孩子指针设置为空
                head.child = null;
                //让最后一个和上层head的下一个拼接
                lastChild.next = nextN;
                if (nextN != null) {
                    nextN.prev = lastChild;
                }
                //准备下一轮，到最后一个  不能到nextN
                head = lastChild;
            }
        }
        return last;
    }
}

方法三：

/*
// Definition for a Node.
class Node {
    public int val;
    public Node prev;
    public Node next;
    public Node child;
};
*/

class Solution {
    public Node flatten(Node head) {
        Node dummy = new Node(-1);
        dummy.next = head;
        while (head != null) {
            //有孩子
            if (head.child != null) {
                Node t = head.next;
                Node child = head.child;
                head.next = child;
                child.prev = head;
                head.child = null;
                //迭代找尾结点
                Node last = child;
                while (last.next != null) {
                    last = last.next;
                }
                last.next = t;
                if (t != null) {
                    t.prev = last;
                }
            } 
            head = head.next;
        }
        return dummy.next;
    }
}