题目链接:6. Z 字形变换
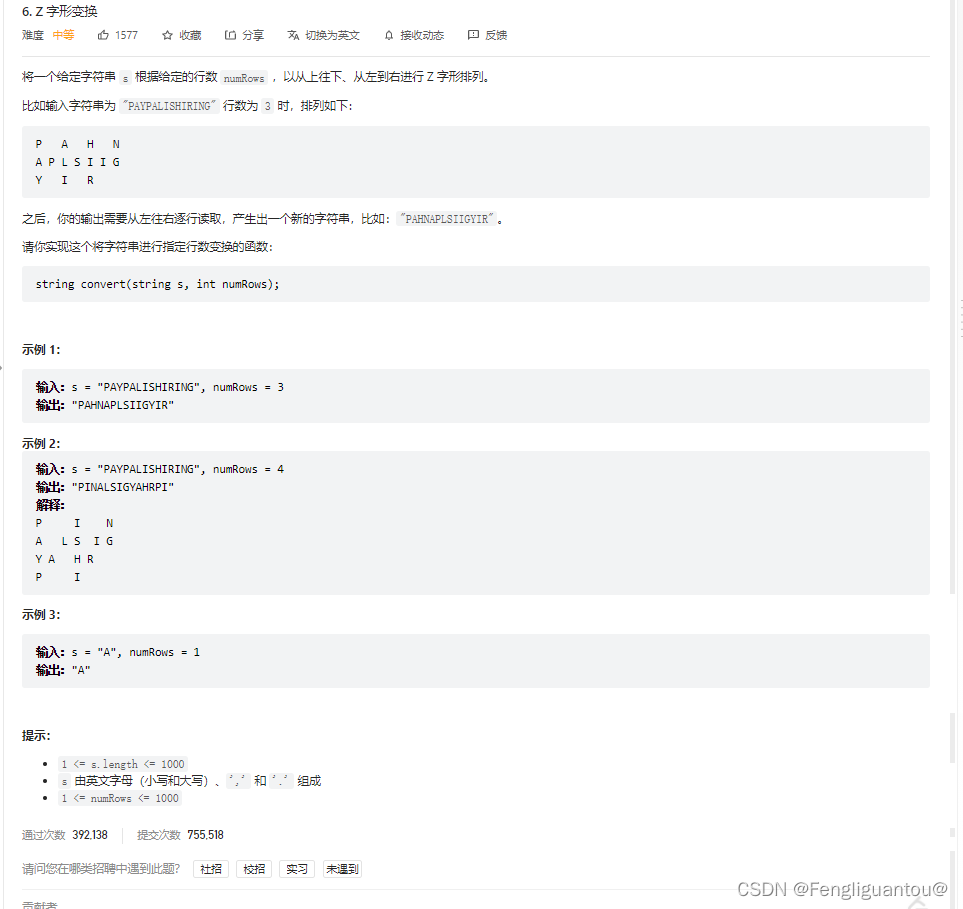
方法一:找规律模拟数组
题目要求构造一个从左到右的Z型矩阵。
通过分析,可以看出这个Z型矩阵的特点
Z型矩阵就是如图中的橙色,绿色这样部分组合在一起的,Z型矩阵就是由一个个这样相同周期组成的。
这里有一种情况需要特殊讨论,当矩阵只有一行时,直接返回原字符。
其余情况均可满足。
其周期的构成满足这样一个规律:
在第一列向下填写矩阵行数r个字符,接着向其右上部分共(r-2)列分别填写一个字符。Z型矩阵的周期t=r+r-2=2*r-2,每个周期会占用矩阵的r-1列,总共有
字符长度len/t个周期(将最后一个周期视作完整周期)。
因此创建一个具有r行c列的的二维矩阵,(这里在计算列的时候需要多+一个周期,因为除法的计算会舍去余数)。一开始从(0,0)这个位置开始填写字符,通过判断i%t与r-1的大小决定向上移动还是向下移动。共两种情况:
i%t<r-1 :说明这时矩阵正在填写第一列的数字,这时只需要向下移动
i%t>=r-1:说明第一列已经填写好了,这时需要向右上方进行填写字符,所以需要向右移动一位,向上移动一位。
当一个周期运行完时,又会回到新周期的第一列。再次遍历矩阵,将存储有字符的位置加入到一个新的字符串中。
class Solution {
public:
string convert(string s, int numRows) {
if(numRows==1||numRows>=s.size())//特殊情况进行排除
return s;
int r=numRows;//矩阵的行数
int t=2*r-2;//周期所含字符个数
int len=s.size();//字符串的长度
int c=(len+t)/t*(r-1);//二维矩阵列数
vector<string> v1 (r,string(c,0));
for(int i=0, x=0,y=0;i<len;i++){
v1[x][y]=s[i];
if(i%t<r-1){
x++;//向下移动
}
else{
x--;//向上移动
y++;//向右移动
}
}
string ans;
for(int i=0;i<r;i++){//遍历矩阵,扫描字符并添加
for(int j=0;j<c;j++){
if(v1[i][j])
ans+=v1[i][j];
}
}
return ans;
}
};
时间复杂度=o(nr)
空间复杂度=o(nr)
方法二:压缩矩阵
在第一种方法,需要构造一个二维矩阵,但是其实只使用了其中的部分空间,这样就导致浪费了许多空间,因此可以对矩阵进行压缩。
依旧是将矩阵只有一行的情况进行额外讨论,若成立,直接返回原字符串。
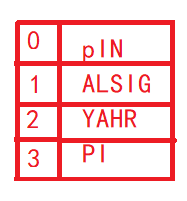
反之,创建一个r行1列的的string数组,通过判断字符i的位置(与第一种方法的判断方式一样),直接将字符填写到数组的对应行。
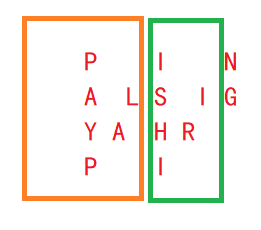
举例说明:
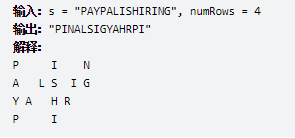
这个Z型字符在模拟数组是这样呈现的:
class Solution {
public:
string convert(string s, int numRows) {
int len=s.size();//字符串长度
int r=numRows;//矩阵行数
int t=2*r-2;//周期所含字符个数
if (r == 1) {
return s;
}
vector<string> v1(r);
int x=0;
for(int i=0;i<len;i++){
v1[x]+=s[i];
if(i%t<r-1)
x++;//向下移动
else
x--;//向上移动
}
string ans;
for (auto &row : v1) {//遍历矩阵,扫描字符并添加
ans += row;
}
return ans;
}
};
时间复杂度:o(n)
空间复杂度:o(n)