目录
🙆堆排序介绍
Heap Sort Origin
斯坦福大学计算及科学系教授罗伯特?弗洛伊德(Robert W. Floyed)和威廉姆斯(J. Williams)在1964年共同发明了堆排序算法。罗伯特?弗洛伊德在芝加哥读的文学,因为找不到工作,改行去当了两年计算机操作员,发现自己对计算机非常感兴趣,后来当了程序员。在弗洛伊德的勤奋好学和深入研究下,1962年他应聘称为卡内基-梅隆大学的副教授,3年后转至斯坦福大学。1970年被聘任为教授。他在计算机的诸多领域:算法、程序设计语言的逻辑和语义,自动程序综合,自动程序验证、编译器的理论和实现等方面做出了创造性的贡献。---百度百科
Heap Introduction
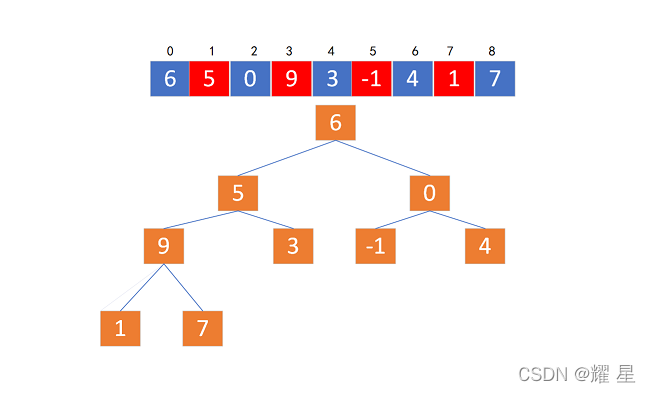
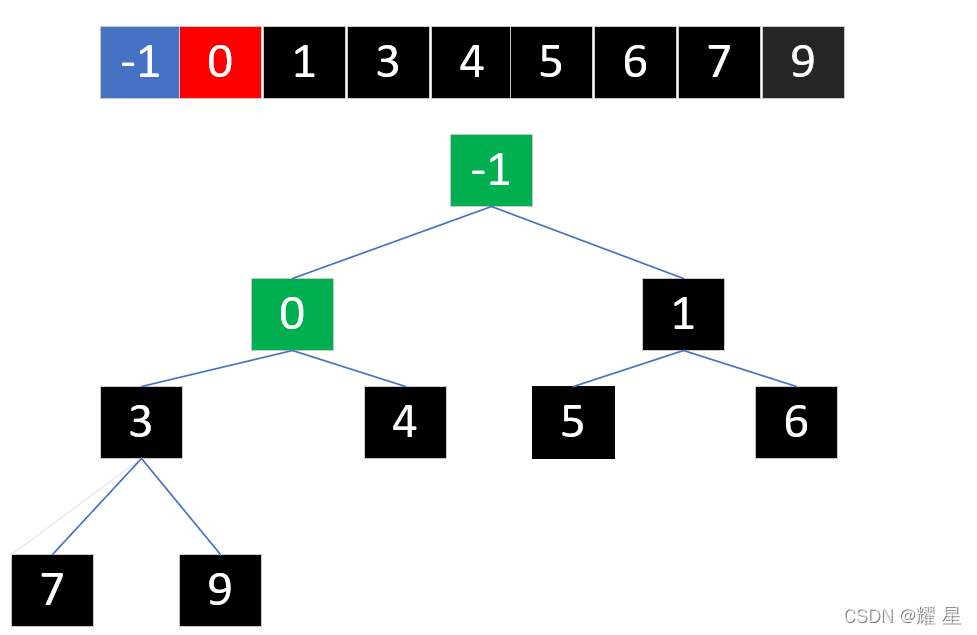
堆是一种非线性数据结构,使用一维数组储存。通过一维数组可以构建出一颗完全二叉树。
堆的逻辑结构是一颗完全二叉树,物理结构是一个数组。
他们之间是如何建立联系的呢?
通过该结点的下标可以找到自己的父亲和左孩子、右孩子。
example:7的下标为8,它的父亲结点的下标就是3,他的左孩子结点是下标为(15>maxIndex)所以7没有左孩子,同理可得也没有右孩子。
堆排序操作图解分析
Built Heap?
大根堆:选出左右孩子结点中较大数和父亲结点进行比较,如果大于父结点则交换,否则不交换。大根堆需要满足的条件:
arr[i] > arr[i*2+1] && arr[i] >arr[i*2+2]?
如何建呢?
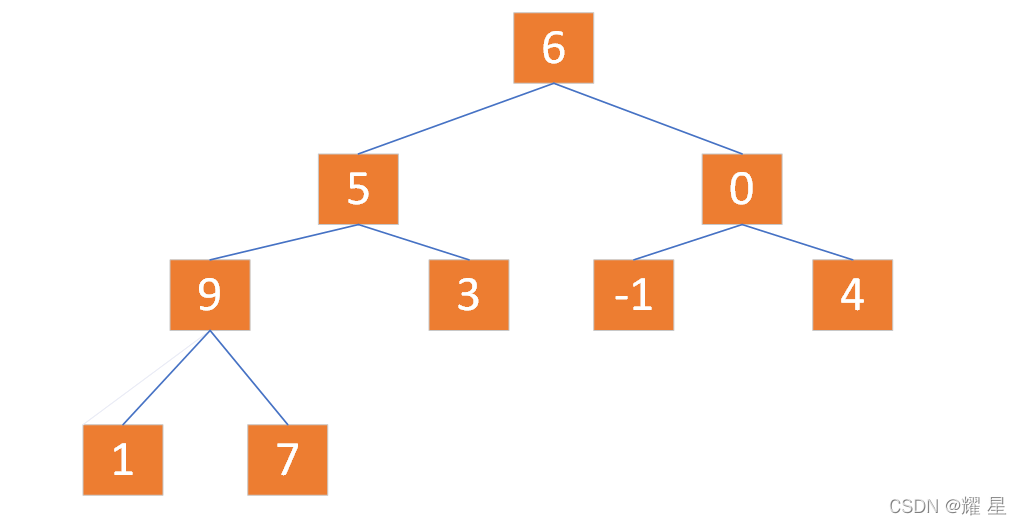
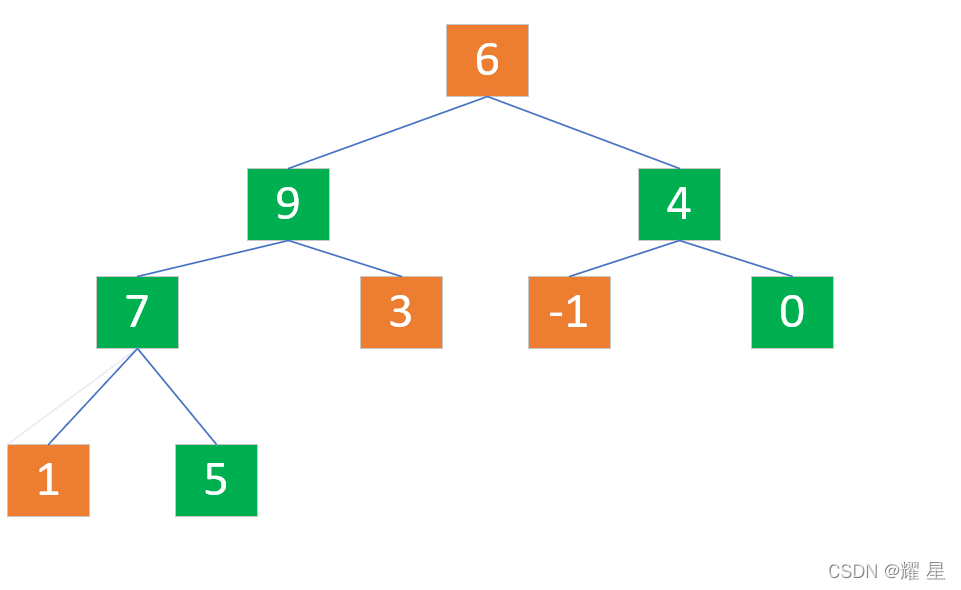
第一次:从parent=3开始建堆,child=parent*2+1。7的父亲结点是9,父亲结点大于子结点,不进行交换。
?第二次:parent=2; 0小于子结点的最大值,4和0交换
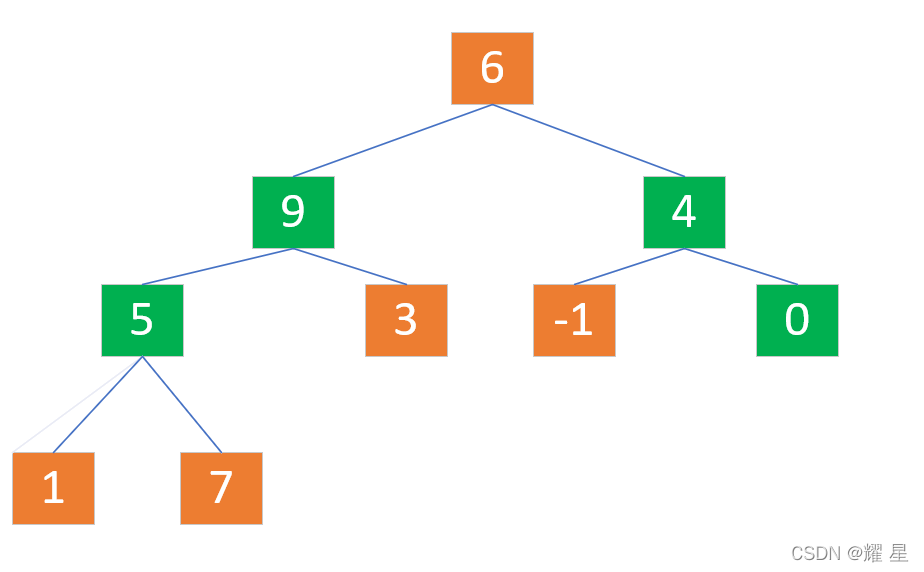
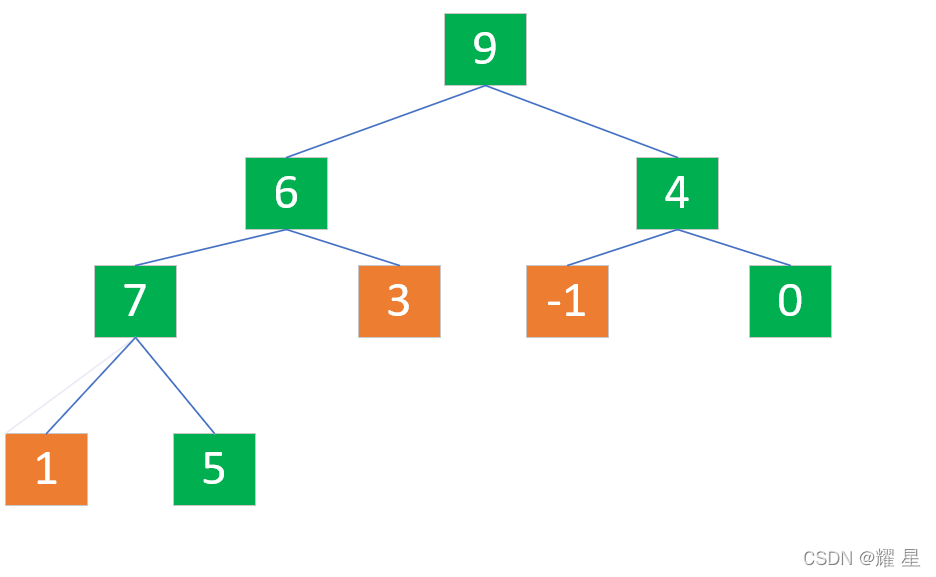
?第三次:parent=1;5小于子结点的最大值,5和9交换。
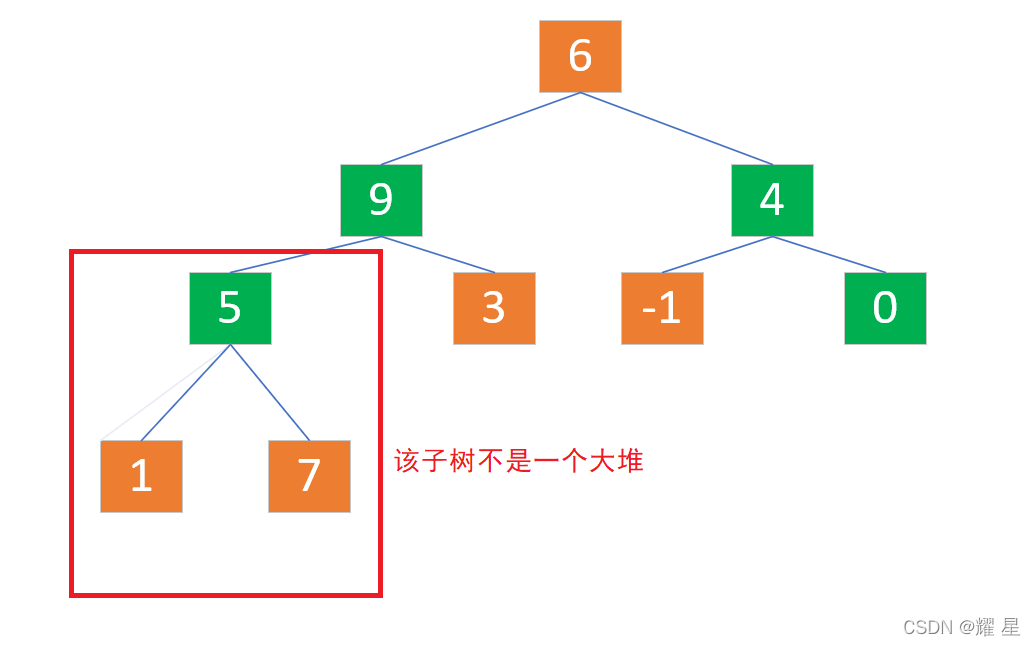
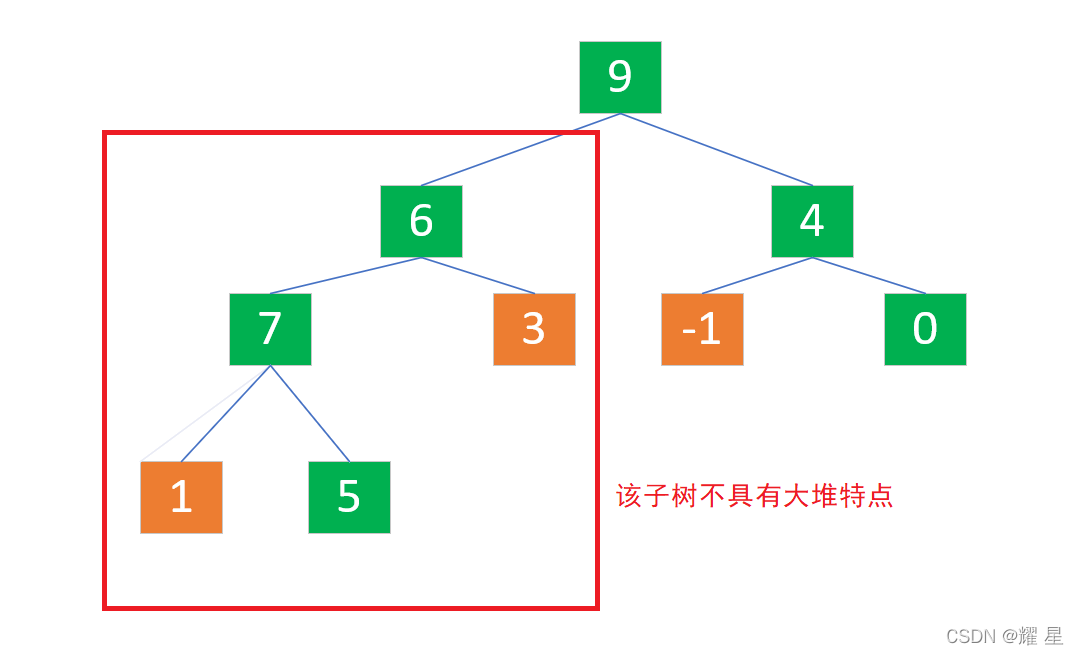
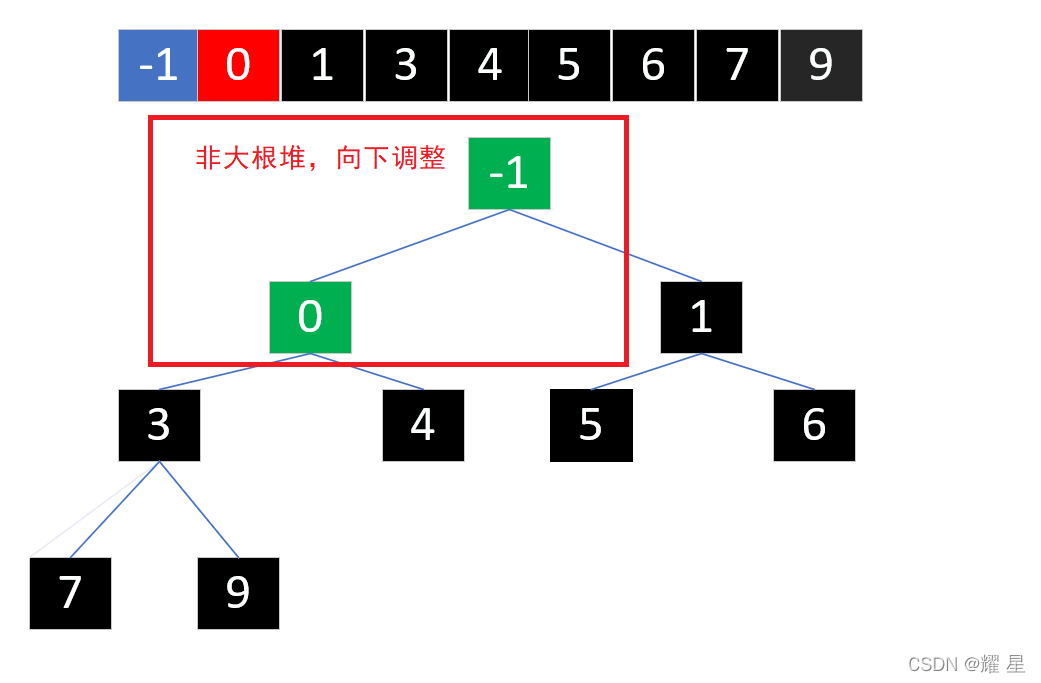
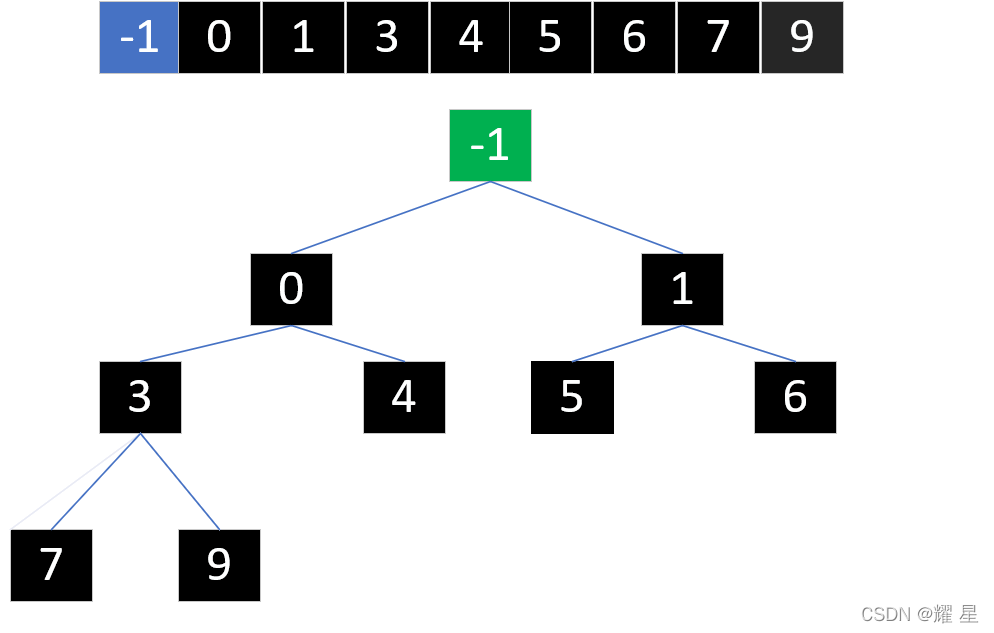
9和5交换过后。你发现了什么。发生这种情况,我们需要向下调整子树(给交换下去的小结点重新建大根堆)。
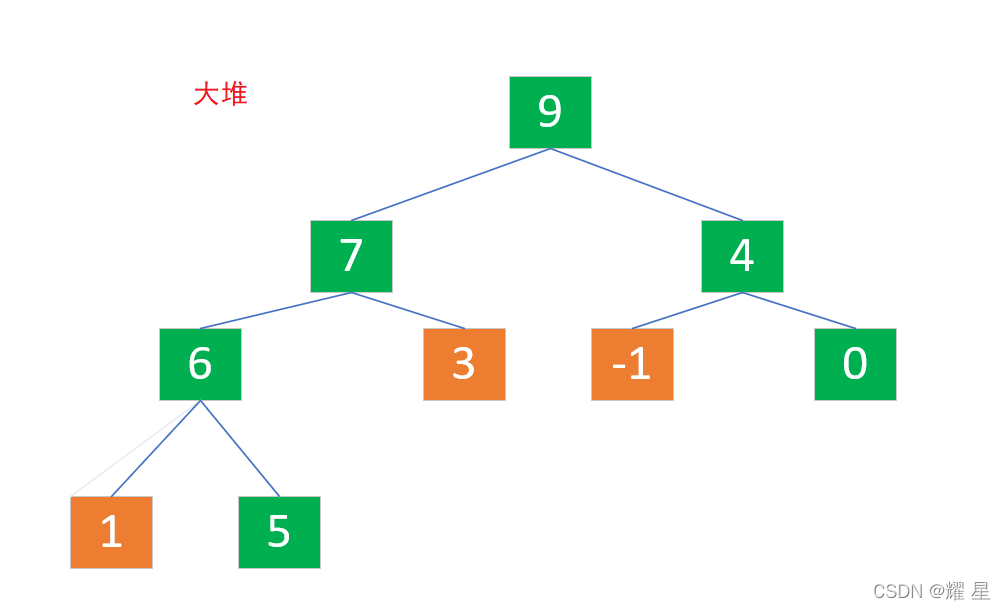
第四次:parent=0;9大于6,所以?9需要和6交换。
我们又发现:需要向下调整子树
void HeapAdjust(int *arr, int n, int parent)//向下调整算法 { int child=parent*2+1;//找到孩子结点 while(child < n) { if(child+1<n && arr[child+1] > arr[child]) { child+=1; } if(arr[parent] < arr[child]) { Swap(&arr[parent],&arr[child]);//交换 } else { break;//如果没有进行交换,就不需要进行向下调整 } parent=child; child=parent*2+1; } return; } void BuiltBigHeap(int *arr,int n) { //从最后一个结点的父亲开始建堆 int end=n-1; int parent=(end-1)/2; while(parent >=0) { HeapAdjust(arr,n,parent); parent--; } return; }
小根堆:选出左右孩子结点中较小数和父亲结点进行比较,如果小于父亲结点则交换,否则不交换。小根堆需要满足的条件:
arr[i]<arr[i*2+1] && arr[i] <arr[i*2+2]
建小根堆和建大根堆类似,大家可以自己尝试建一个小根堆。
注意:那么堆排序用建大根堆的方式还是建小根堆的方式呢?
答案:建大根堆,建大根堆不会破坏所有子树的大根堆结构。
Sort
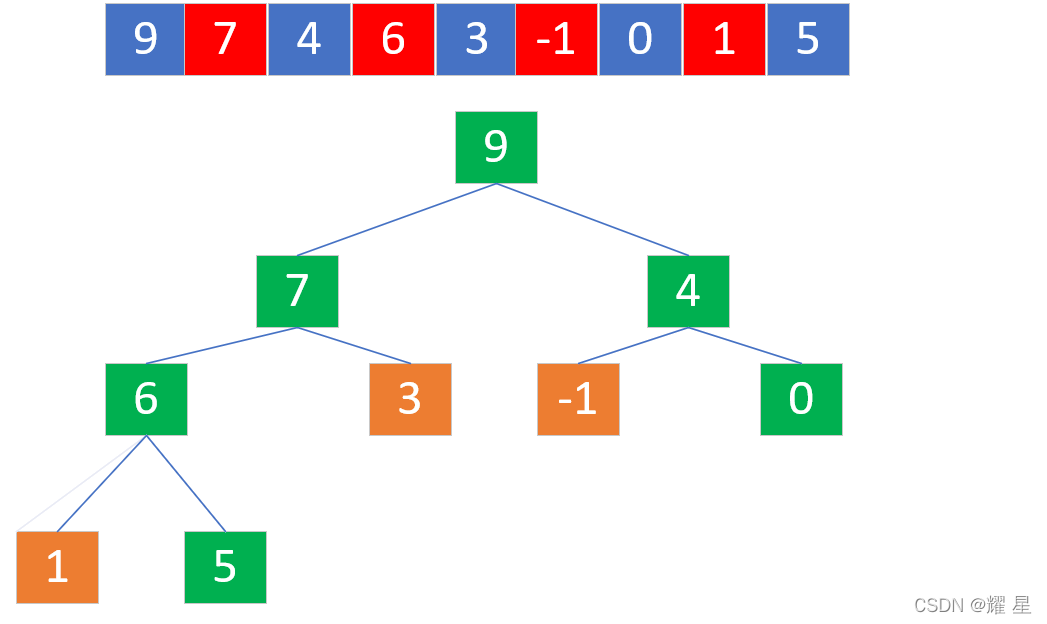
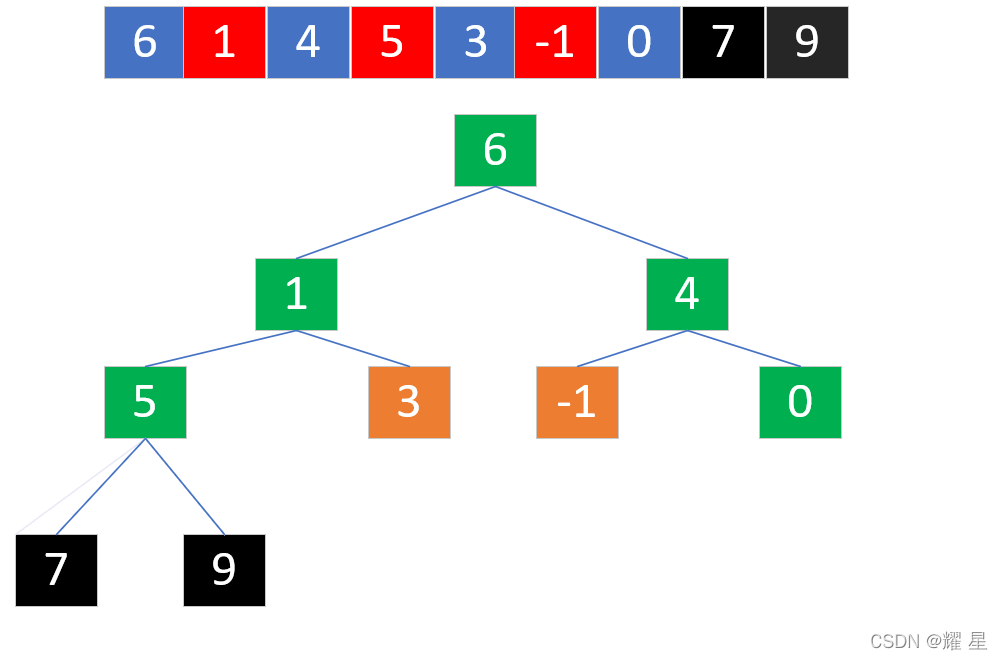
建立了大根堆,我们就能选择出堆中最大元素,将堆中的最大元素和堆中的最后一个结点进行交换。
example:
?提示:黑色部分代表已经排好序的部分,不参与向下调整。
?
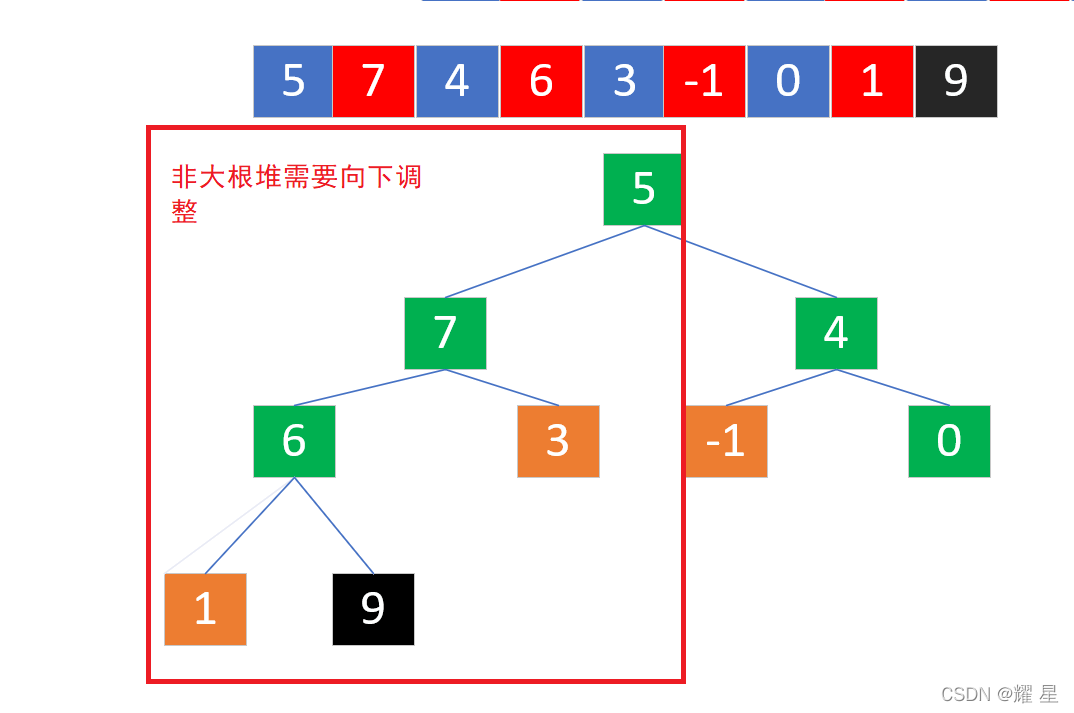
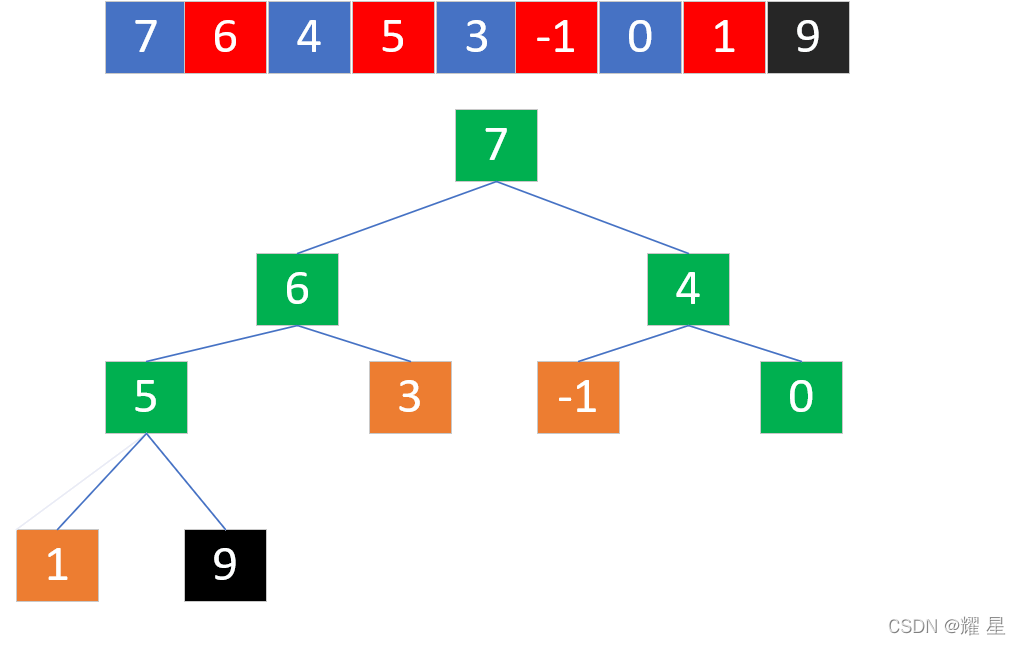
?选出最大值,和1进行交换。
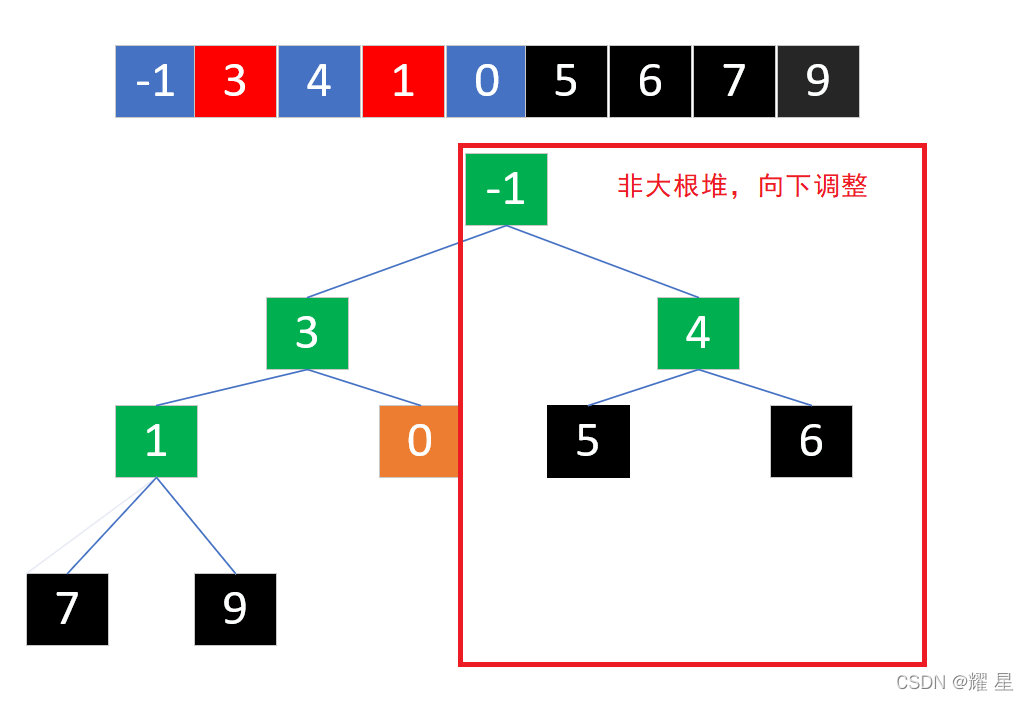
?
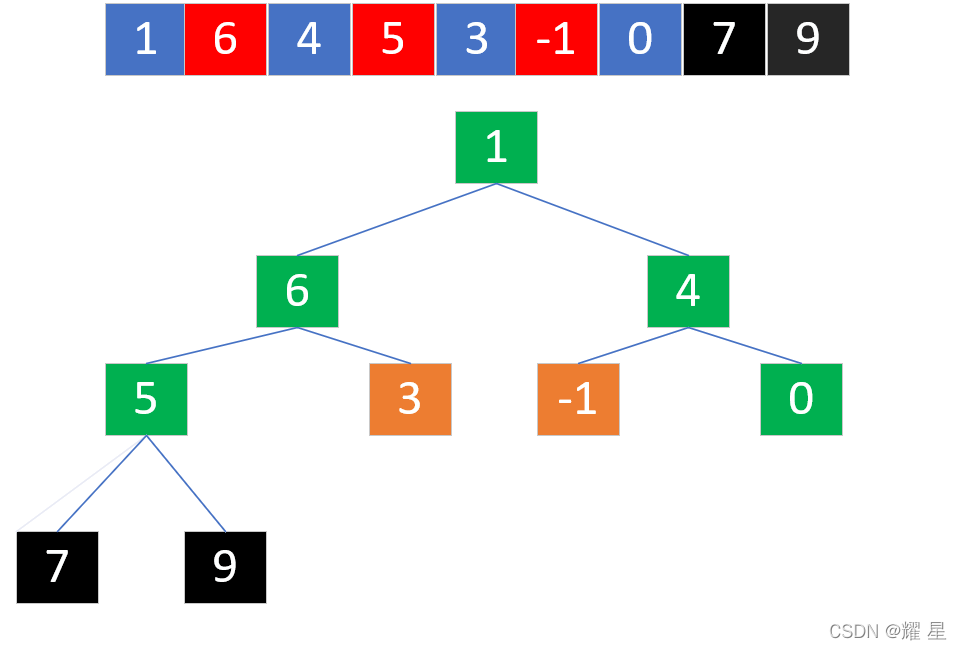
?选出最大值,和0进行交换
?
?选出最大值,5和-1交换
?
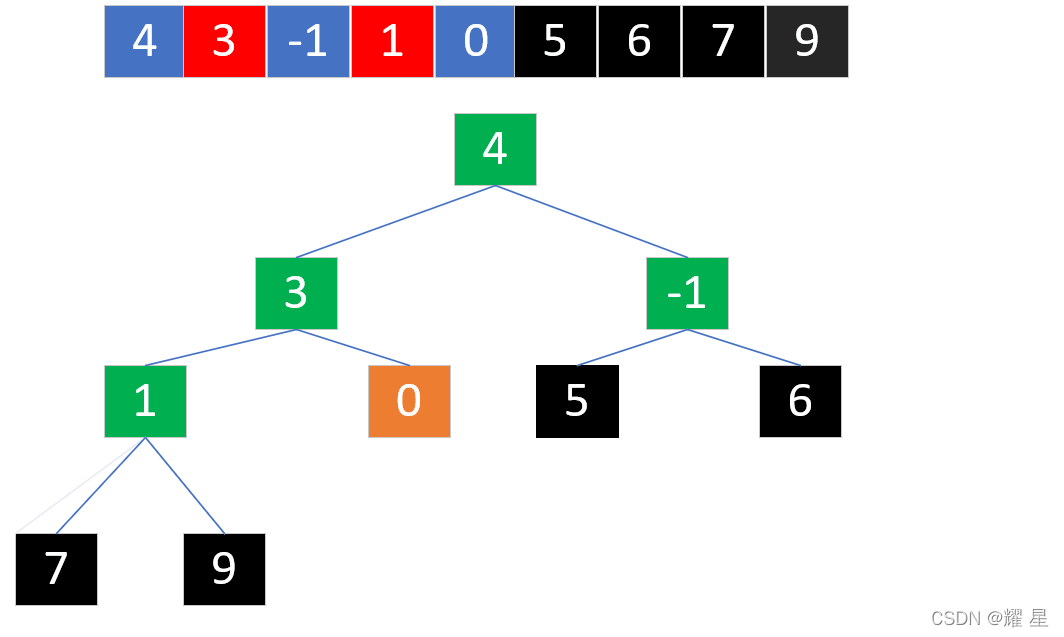
?
?选出最大值,将4和0进行交换
?
?
?
选出最大值,3和0进行交换
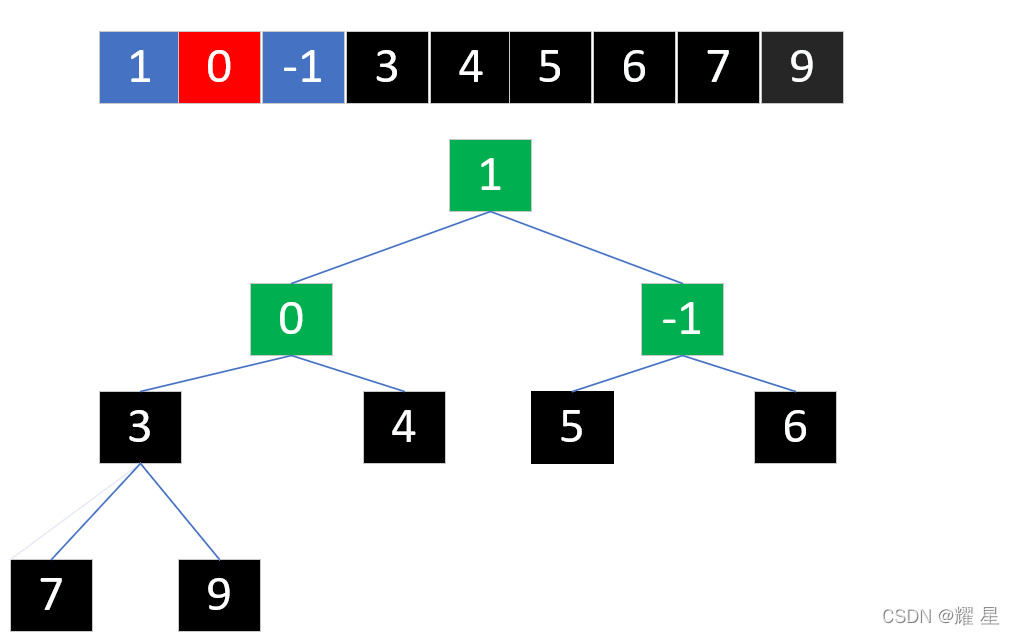
?
选出最大值,1和-1交换?
?选出最大值,0和-1交换
当还剩一个未排序结点时,结束调整,排序结束!?
🎈堆排序实现
void HeapSort(int *arr, int n)
{
int end=n-1;
BuiltHeap(arr, n);
while(end > 0)
{
Swap(&arr[end],&arr[0]);//将最大值置于数组末
end--;
HeapAdjust(arr,end,0);//从根结点向下调整
}
return;
}😳时间复杂度分析
我们依次来分析建大根堆,向下调整算法,堆排序的时间复杂度。
向下调整算法:我们设树的高度为h,k为层次。
?从根结点向下调整。
向下调整时,每一层只会选一颗子树的结点进行交换,有n个结点的完全二叉树,深度为
向下调整算法的时间复杂度是(
)
建立一颗大根堆的时间复杂度是
堆排序的时间时间复杂度是:
希望大家在阅读后能够有所收获,能力有限,有误的地方还请大佬指点指点,谢谢大家的支持!