leetcode之动态规划刷题总结7
动态规划(英语:Dynamic programming,简称 DP)是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
动态规划常常适用于有重叠子问题和最优子结构性质的问题,并且记录所有子问题的结果,因此动态规划方法所耗时间往往远少于朴素解法。
动态规划有自底向上和自顶向下两种解决问题的方式。自顶向下即记忆化递归,自底向上就是递推。
使用动态规划解决的问题有个明显的特点,一旦一个子问题的求解得到结果,以后的计算过程就不会修改它,这样的特点叫做无后效性,求解问题的过程形成了一张有向无环图。动态规划只解决每个子问题一次,具有天然剪枝的功能,从而减少计算量。
1-最长定差子序列
题目链接:题目链接戳这里!!!
思路:动态规划
由于我们总是在左侧找一个最近的等于arr[i]?difference 元素并取其对应dp 值,因此我们直接用 dp[num] 表示以 num为结尾的最长的等差子序列的长度,这样 dp[num?difference] 就是我们要找的左侧元素对应的最长的等差子序列的长度.
class Solution {
public int longestSubsequence(int[] arr, int difference) {
Map<Integer, Integer> map = new HashMap<>() ;
int ans = 0 ;
for(int num : arr){
map.put(num, map.getOrDefault(num-difference,0)+1) ;
ans = Math.max(ans,map.get(num)) ;
}
return ans ;
}
}

2-不相交的直线
题目链接:题目链接戳这里!!!
思路:动态规划
这一题刚看的时候感觉很牛的样子,仔细一看,发现就是求两个数组的最长公共子序列,dp[i][j]表示nums1[0;i]与nums[0:j]的最长公共子序列。
我们很容易得到递推表达式:
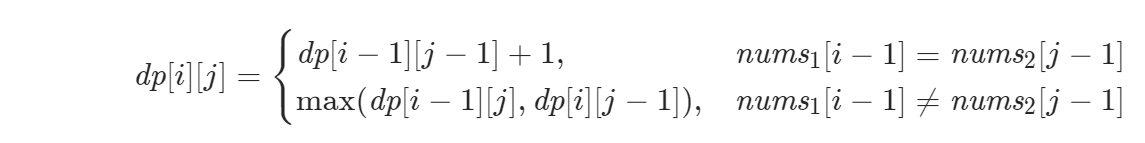
class Solution {
public int maxUncrossedLines(int[] nums1, int[] nums2) {
//其实就是求nums1数组和nums2数组的最长公共子序列
int n = nums1.length , m = nums2.length ;
int [][] dp = new int [n+1][m+1] ;
for(int i=1; i<=n; i++){
int x = nums1[i-1] ;
for(int j=1; j<=m; j++){
int y = nums2[j-1] ;
if(x==y){
dp[i][j] = dp[i-1][j-1] + 1 ;
}else{
dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]) ;
}
}
}
return dp[n][m] ;
}
}

3-字符串的好分割数目
题目链接:题目链接戳这里!!!
思路:使用left数组和right数组分别记录左边和右边不同字母对应得个数,初始时左边为空串,右边为整个字符,用a,b变量记录左右得不同字符串得个数。
class Solution {
public int numSplits(String s) {
//分别使用left数组和right数组记录左边和右边不同字符的个数
int [] left = new int [26] ;
int [] right = new int [26] ;
int ans = 0 ;
for(int i=0; i<s.length(); i++){
right[s.charAt(i)-'a'] ++ ;
}
int a=0, b=0 ;
for(int i=0; i<26; i++){
if(left[i] > 0){
a ++ ;
}
if(right[i]>0){
b ++ ;
}
}
for(int i=0; i<s.length(); i++){
if(left[s.charAt(i)-'a']==0){
left[s.charAt(i)-'a'] ++ ;
a ++ ; //累记左边不同字符的个数
}
if(--right[s.charAt(i)-'a']==0){
b -- ; //累记右边不同字符的个数
}
if(a == b){
ans ++ ;
}
}
return ans ;
}
}

4-可被3整除得最大和
题目链接:题目链接戳这里!!!
思路:动态规划思想,使用数组remainder[0]记录对3取余等于0的最大和,remainder[1]记录对3取余等于1的最大和,remainder[2]记录对3取余等于2的最大和。
class Solution {
public int maxSumDivThree(int[] nums) {
int n = nums.length ;
int [] remiander = new int [3] ;
for(int i=0; i<nums.length; i++){
int a = nums[i] + remiander[0] ;
int b = nums[i] + remiander[1] ;
int c = nums[i] + remiander[2] ;
remiander[a%3] = Math.max(a,remiander[a%3]) ;
remiander[b%3] = Math.max(b,remiander[b%3]) ;
remiander[c%3] = Math.max(c,remiander[c%3]) ;
}
return remiander[0] ;
}
}

5-统计全为1的正方形子矩阵
题目链接:题目链接戳这里!!!
思路:dp[i][j]表示以(i,j)为右下标的正方形数目,我们仔细思考一下可以得到如下状态转移方程:
图中f[i][j]即为dp[i][j]

class Solution {
public int countSquares(int[][] matrix) {
//dp[i][j]表示以(i,j)为右下角的正方形数目
int m = matrix.length ;
int n = matrix[0].length ;
int [][] dp = new int [m][n] ;
int ans = 0 ;
for(int i=0; i<m; i++){
for(int j=0; j<n; j++){
if(i==0 || j==0){
dp[i][j] = matrix[i][j] ;
}else if(matrix[i][j] == 0){
dp[i][j] = 0 ;
}else{
dp[i][j] = Math.min(dp[i-1][j],Math.min(dp[i-1][j-1],dp[i][j-1])) + 1 ;
}
ans += dp[i][j] ;
}
}
return ans ;
}
}

**
3月37日,4月9日,两场contest,希望多一点AC,少一点WA,冲吧.
**