[数据结构与算法]快速排序算法分析与Java实现

算法思想

快速排序基于分治法

• 在待排序列L[1…n]中任取一个元素为基准，
• 通过依然排序将待排序表划分为独立的两部分L[1…k-1]和L[k+1…n]，
• 使得L[1…k-1]中的所有元素小于pivot，L[k+1…n]中的所有元素大于或等于pivot，则pivot被放在了最终的位置上。
• 然后递归地对两个子表重复上述过程，直到每部分只有一个元素或空为止，即所有的元素都放到了最终位置上。

结合例子对算法分析

以数组{7, 1, 2, 10, 6, 4, 3, 5, 9, 8}为例子分析算法执行的流程

• 第一步
  初始化low，high指针
  初始化pivot为数组的第一个元素
  high指针往左移动，找到第一个小于pivot的元素
  

• 第二步
  将第一个小于pivot的元素放到low指针指向的位置
  

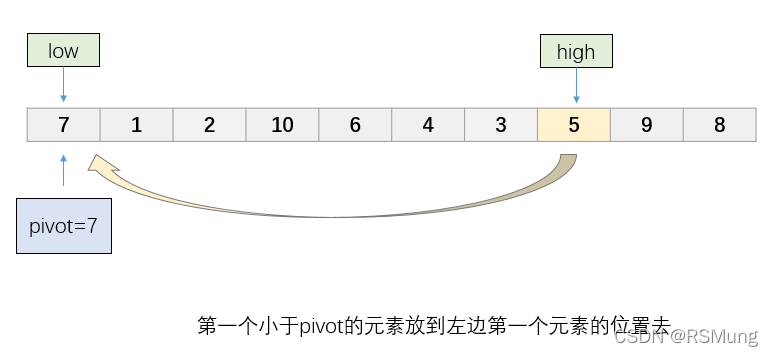
• 第三步
  low指针开始往右侧移动，寻找第一个大于pivot的元素
  

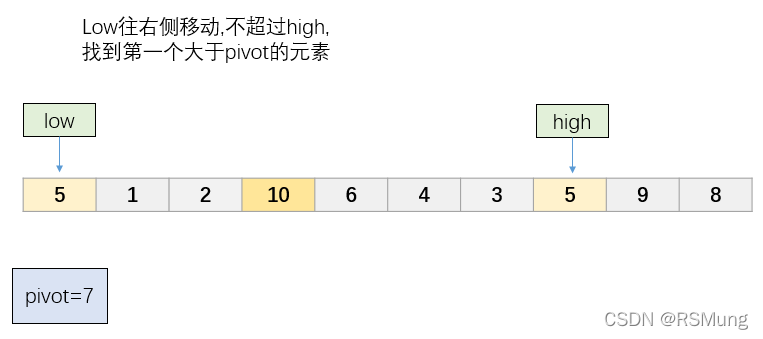
• 第四步
  将找到的第一个大于pivot的元素移动到high指针指向的位置
  

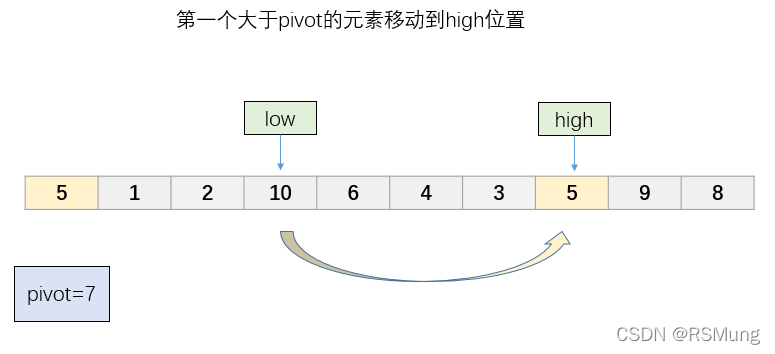
• 第五步
  high指针往左移动，找到第一个小于pivot的元素
  

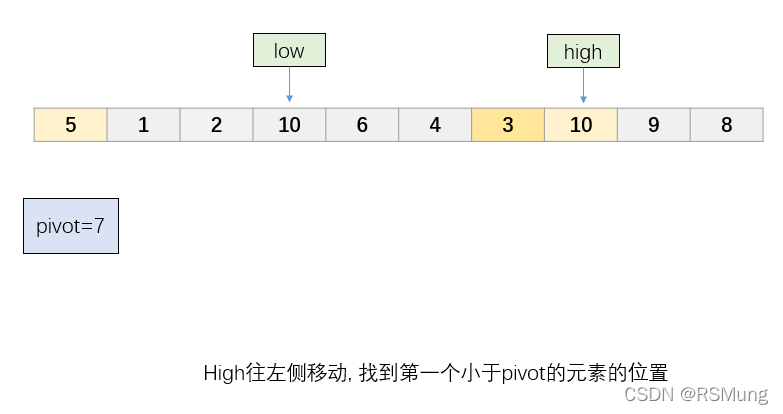
• 第六步
  将找到的第一个小于pivot的元素移动到low指针指向的位置
  

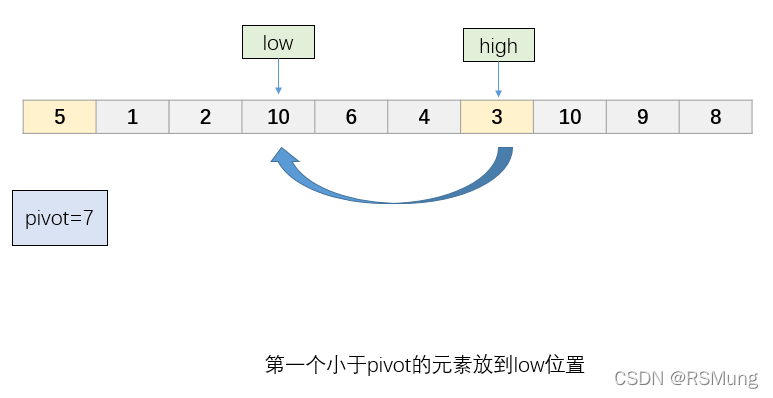
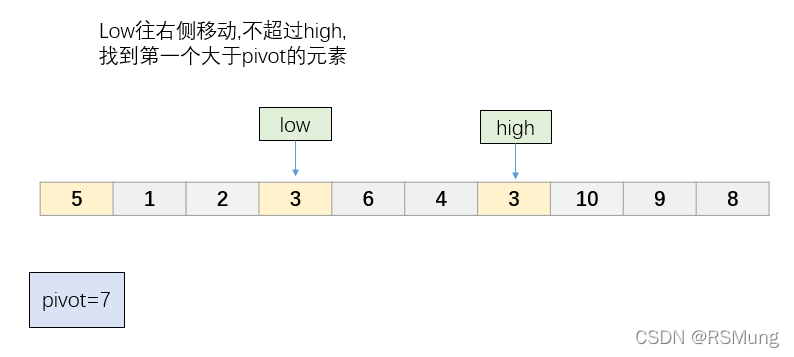
• 第七步
  low指针往右侧移动， 寻找第一个大于pivot的元素
  此时已经不存在了， 因此low指针移动到high指针的位置就结束了寻找的循环了。
  
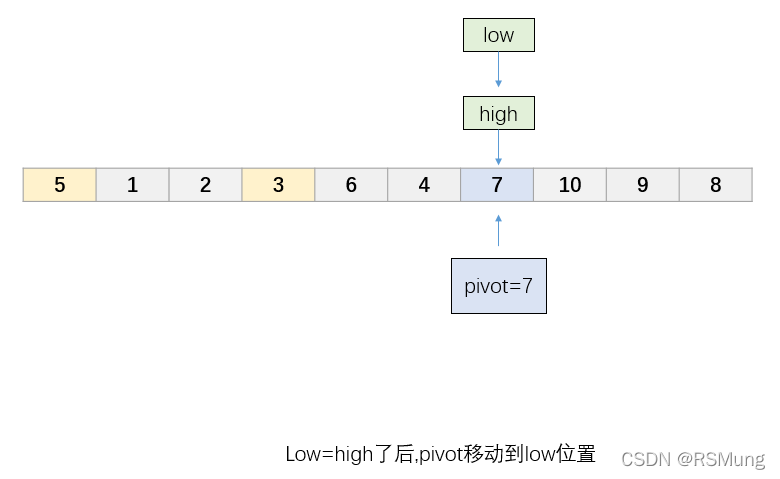
  最后将pivot放在low指针（也是high指针）所在的位置，pivot这个元素就被放在最终的位置上了。
  pivot左边的元素都小于它，右边的元素都大于它。
  之后再对两个子表分别递归地进行快速排序就可以了。
  

总结

根据我对上述的例子的观察，快速排序的关键在于选定后pivot对元素的移动。
整体来说以
high指针往左侧移动，将碰到的第一个小于pivot的元素放到low指针位置；
low指针往右侧移动，将碰到的第一个大于pivot的元素放到high指针位置；
这样两个循环为一个单位操作。
多个这样的单位操作后就会出现low指针与high指针重合的情况，此时就可以将pivot放到low指针位置，即将pivot代表的元素放到了最终的位置上了。

快速排序的空间复杂度分析

因为使用了递归，所以存在递归工作栈。
最好的情况下栈的深度为$?lo{g}_2(n+1)?$，最坏情况下要进行n-1次递归调用，栈的深度为O(n)
因此空间复杂度最坏是O(n)，最好是O($lo{g}_{2}n$)

快速排序的时间复杂度分析

时间效率与划分是否对称有关，最坏情况是两个区域分别包含n-1个元素和0个元素，对应于待排序表基本有序或者逆序的情况。
最坏情况下时间复杂度O($n^2$)

最理想的划分下，两个区域差不多大，单个不可能大于n/2
此时时间复杂度为O(n$lo{g}_{2}n$)

快速排序算法平均情况下的效率与最好情况下的效率接近，因此它是所有内部排序算法中平均性能最优的排序算法。

Java代码实现

/**
* 快速排序
* 时间复杂度:pivot划分最平衡时最好O(nlog2n), 序列基本有序或者逆序时最坏O(n^2)
* 空间复杂度最好时O(log2n), 最坏时O(n)
* */
public static String quickSort(int[] originalData){
	quickSortProcess(originalData, 0, originalData.length-1);
	return Arrays.toString(originalData);
}

/**
* 快速排序的主流程
* */
public static void quickSortProcess(int[] data, int low, int high){
	//序列只有一个元素或空是递归的结束条件
	if(low < high){
		//选取pivot并且使得左侧小于pivot,右侧大于pivot
	    int pivot = quickSort_Partition(data, low, high);
	    quickSortProcess(data, low, pivot-1);//让左侧子表有序
	    quickSortProcess(data, pivot+1, high);//让右侧子表有序
	}
}

/**
* 快速排序选取基准的方法
* @return 基准pivot所在的位置
* */
public static int quickSort_Partition(int[] data, int low, int high){
	int pivot = data[low];
	while(low < high){
    	//high向左移动,找到第一个小于pivot的元素
		while(low < high && data[high] >= pivot){
			high--;
		}
    	//将第一个小于pivot的元素放到low位置
		data[low] = data[high];
    	//low向右移动,找到第一个大于pivot的元素
		while(low < high && data[low] <= pivot){
			low++;
		}
    	//将第一个大于pivot的元素放到high位置
		data[high] = data[low];
	}
	//此时low与high相等,将pivot放到这个位置即可
	data[low] = pivot;
	return low;
}