Task09:排序
0. 相关博客
我在之前的Python程序员面试笔试宝典专栏的第4章_数据结构与算法(一)博客当中,总结过十大排序算法
1. 视频题目
1.1 合并两个有序数组
1.1.1 描述
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出:[1,2,2,3,5,6]
解释:需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。
示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0
输出:[1]
解释:需要合并 [1] 和 [] 。
合并结果是 [1] 。
示例 3:
输入:nums1 = [0], m = 0, nums2 = [1], n = 1
输出:[1]
解释:需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意,因为 m = 0 ,所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。
提示:
nums1.length==m + n
nums2.length == n
0 <= m, n <= 200
1 <= m + n <= 200
-109 <= nums1[i], nums2[j] <= 109
进阶:你可以设计实现一个时间复杂度为 O(m + n) 的算法解决此问题吗?
1.1.2 代码
本题要求的是在原数组上进行修改,否则直接新建一个数组,然后扫描两个原数组即可
原数组后面为空,两个数组有序,所以是从后往前扫描,并且从后往前插入原数组
class Solution:
def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
"""
Do not return anything, modify nums1 in-place instead.
"""
i = m+n-1
n1 = m-1
n2 = n-1
while n2>-1 and n1>-1:
if nums1[n1]<nums2[n2]:
# 如果是nums2的值更大
nums1[i] = nums2[n2]
n2 -= 1
# nums2的指针左移弹出元素
else:
# 否则就是相等或者nums1更大
nums1[i] = nums1[n1]
n1 -= 1
# 弹出nums1的元素
i -= 1
# 新数组的指针左移
nums1[0:n2+1] = nums2[0:n2+1]
# 如果nums2还有值的话
1.1.3 总结
可以从大到小,从后往前扫描,因为原数组的后面是空的
1.2 排序数组
1.2.1 描述
给你一个整数数组 nums,请你将该数组升序排列。
示例 1:
输入:nums = [5,2,3,1]
输出:[1,2,3,5]
示例 2:
输入:nums = [5,1,1,2,0,0]
输出:[0,0,1,1,2,5]
提示:
1 <= nums.length <= 5 * 104
-5 * 104 <= nums[i] <= 5 * 104
1.2.2 代码
先来试试归并排序
class Solution:
def merge(self,nums1,nums2):
res = []
while nums1 and nums2 :
if nums1[0] < nums2[0]:
res.append(nums1.pop(0))
# 升序排列,先加入小的
else:
res.append(nums2.pop(0))
res += nums1
# 如果nums1非空就连接,此时nums2肯定为空
res += nums2
# 如果nums2非空就连接,此时nums1肯定为空
return res
def mergeSort(self,nums):
if len(nums)>1 :
# 如果数组中至少两个元素
mid = len(nums)//2
# 求得中值,划分左右
return self.merge(self.mergeSort(nums[0:mid]),self.mergeSort(nums[mid:]))
# 合并排序后的左右数组
else:
return nums
# 只有一个元素就认为是排序好的结果,直接返回
def sortArray(self, nums: List[int]) -> List[int]:
return self.mergeSort(nums)
快排的时候有点神奇,对于同一个思路:
class Solution:
def quickSort(self,nums):
if len(nums)>1:
mid = len(nums)//2
left = []
right = []
mid = nums.pop(mid)
while nums:
if nums[0]<mid:
left.append(nums.pop(0))
# 小的加入左边
else:
right.append(nums.pop(0))
#大的加入右边,相等的也在右边
return self.quickSort(left)+[mid]+self.quickSort(right)
# 返回排序好的数组
else:
return nums
# 只有一个元素则认为有序
def sortArray(self, nums: List[int]) -> List[int]:
return self.quickSort(nums)
上面的写法是超时的,下面的写法才正常
class Solution:
def quickSortV1(self,array):
if len(array) < 2:
return array
# 数组只有一个值则返回
mid = array[len(array) // 2]
# 选取基准,随便选哪个都可以
left, right = [], []
# 定义基准值左右两个数列
array.remove(mid)
# 从原始数组中移除基准值
for item in array:
if item >= mid:
right.append(item)
# 大于基准值放右边
else:
left.append(item)
# 小于基准值放左边
return self.quickSortV1(left) + [mid] + self.quickSortV1(right)
# 递归对新数组的左右两边进行排序
def sortArray(self, nums: List[int]) -> List[int]:
return self.quickSortV1(nums)
应该是pop涉及到了对原数组的修改,所以比较耗费实践
1.2.3 总结
只有一个元素的数组被认为是有序的,这也是递归的出口
快排的时候不要修改原数组,很费时间的,用for遍历就好
2. 作业题目
2.1 有序数组的平方
2.1.1 描述
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例 1:
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100]
排序后,数组变为 [0,1,9,16,100]
示例 2:
输入:nums = [-7,-3,2,3,11]
输出:[4,9,9,49,121]
提示:
1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 已按 非递减顺序 排序
进阶:
请你设计时间复杂度为 O(n) 的算法解决本问题
2.1.2 代码
应该是分为正数序列和负数序列来处理,正序列左到右,负序列右到左,都保证平方后是递增
然后比较得出平方较小的那一个数字,将其平方值放入到结果的列表当中
如果序列未完结,则逐个平方后按升序方向合并进入结果数组
注意,这里的序列是否完结需要判断,不然后面数组的索引可能会出错
也就是说,要保证数组的索引是真实有效不越界的
class Solution:
def sortedSquares(self, nums: List[int]) -> List[int]:
res = []
i = 0
while i<len(nums):
if nums[i]<0:
i+=1
else:
break
# 找到第一位非负数
if i > 0:
j = i-1
# 如果存在负数
else:
j = -1
# 不存在负数则置为-1
while -1<j and i<len(nums):
# 当正负序列都有值
if nums[j]**2 < nums[i]**2 :
res.append(nums[j]**2)
j -= 1
# 负数的平方更小
else :
res.append(nums[i]**2)
i += 1
# 正数的平方更小
if -1<j:
res += [i**2 for i in nums[0:j+1]][::-1]
# 负数序列未完结
if i<len(nums):
res += [i**2 for i in nums[i:len(nums)]]
# 整数序列未完结
return res
2.1.3 总结
在有序的前提下,正序列左到右平方,负序列右到左平方,都保证平方后是递增
像数组索引这种情况,一定要优先保证索引是真实有效的再去进行使用
2.2 数组的相对排序
2.2.1 描述
给你两个数组,arr1 和 arr2,arr2 中的元素各不相同,arr2 中的每个元素都出现在 arr1 中。
对 arr1 中的元素进行排序,使 arr1 中项的相对顺序和 arr2 中的相对顺序相同。未在 arr2 中出现过的元素需要按照升序放在 arr1 的末尾。
示例 1:
输入:arr1 = [2,3,1,3,2,4,6,7,9,2,19], arr2 = [2,1,4,3,9,6]
输出:[2,2,2,1,4,3,3,9,6,7,19]
示例 2:
输入:arr1 = [28,6,22,8,44,17], arr2 = [22,28,8,6]
输出:[22,28,8,6,17,44]
提示:
1 <= arr1.length, arr2.length <= 1000
0 <= arr1[i], arr2[i] <= 1000
arr2 中的元素 arr2[i] 各不相同
arr2 中的每个元素 arr2[i] 都出现在 arr1 中
2.2.1 代码
利用哈希映射的思想,我们给原数组赋予权重,然后根据映射的权重表进行排序,再还原
我们需要将arr2的数值放在前面,不在arr2的放在后面,也就是arr2的权重小于正常权重
我们对于正常数字,直接将其本身作为权重,而对于arr2,则根据顺序从-5000赋予权重
其实这个-5000也可以改为别的,只要使得arr2中最大的权重,小于正常数字最小的权重就好
正常数字最小应该是0,所以arr2的权重最大为-1
而arr2最长有1000位,所以起始权重最大为-1000
我们构造第一个字典dict1记录arr2及其对应权重,而dict2则记录各权重对应的数字
至于hashTable,是arr1各数字映射的权重表,对其进行排序再还原即可,能够处理重复值
class Solution:
def quickSort(self,nums):
if len(nums)>1:
# 如果数组当中超过一个元素
mid = nums.pop(len(nums)//2)
left = []
right = []
for item in nums:
if item < mid :
left.append(item)
else:
right.append(item)
return self.quickSort(left)+[mid]+self.quickSort(right)
else:
# 数组当中少于两个元素即为有序
return nums
def relativeSortArray(self, arr1: List[int], arr2: List[int]) -> List[int]:
val = -5000
hashTable = []
dict1 = dict()
# 记录arr2当中数值的权重
val = -5000
# 权重的数值
for item in arr2:
dict1[item] = val
val += 1
# 先出现的数字的权重更小
hashTable = []
# 记录arr1数字的权重,用于排序
dict2 = dict()
# 记录arr1权重对应的数字,用于还原
for item in arr1:
if item in arr2:
# 如果在arr2当中
hashTable.append(dict1[item])
# 其权重就是dict1的权重
dict2[dict1[item]] = item
# 记录权重对应的数字
else :
# 不在arr2当中
hashTable.append(item)
# 其权重就是自身
dict2[item] = item
# 记录权重对应的数字
sortedTable = self.quickSort(hashTable)
# 对权重表进行排序
return [dict2[item] for item in sortedTable]
# 根据权重的排序结果,还原原数组
2.2.3 总结
无法直接对数字进行排序,我们可以考虑对其赋予权重,然后根据权重来排序
权重表的数字和原数组的值是一一对应的,所以即使是重复值也可以处理
2.3 对链表进行插入排序
2.3.1 描述
给定单个链表的头 head ,使用 插入排序 对链表进行排序,并返回 排序后链表的头 。
插入排序 算法的步骤:
插入排序是迭代的,每次只移动一个元素,直到所有元素可以形成一个有序的输出列表。
每次迭代中,插入排序只从输入数据中移除一个待排序的元素,找到它在序列中适当的位置,并将其插入。
重复直到所有输入数据插入完为止。
下面是插入排序算法的一个图形示例。部分排序的列表(黑色)最初只包含列表中的第一个元素。每次迭代时,从输入数据中删除一个元素(红色),并就地插入已排序的列表中。
对链表进行插入排序。
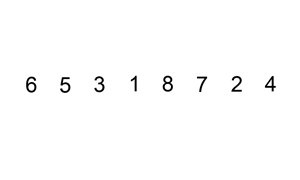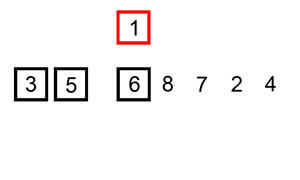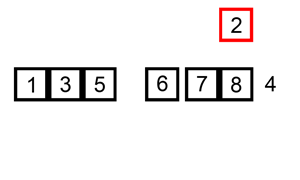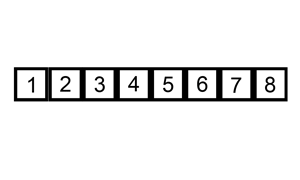
示例 1:
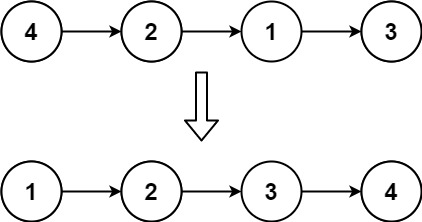
输入: head = [4,2,1,3]
输出: [1,2,3,4]
示例 2:
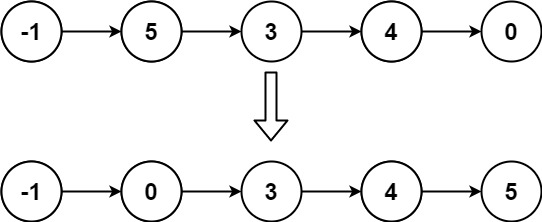
输入: head = [-1,5,3,4,0]
输出: [-1,0,3,4,5]
提示:
列表中的节点数在 [1, 5000]范围内
-5000 <= Node.val <= 5000
2.3.2 代码
新建一个列表,然后扫描原列表,将数值插入到新列表的合适的位置
在新列表当中寻找合适的位置的时候,一般使用.next来与当前元素比较
class Solution:
def insertionSortList(self, head: ListNode) -> ListNode:
dummy = ListNode()
dummy.next = head
cur = head.next
head.next = None
while cur:
curNext = cur.next
insertP = dummy
while insertP.next and cur.val > insertP.next.val:
insertP = insertP.next
cur.next = insertP.next
insertP.next = cur
cur = curNext
return dummy.next
2.3.3 总结
在新列表当中寻找合适的位置的时候,一般使用.next来与当前元素比较