Given the root of a binary tree, return the number of uni-value subtrees.
A uni-value subtree means all nodes of the subtree have the same value.
Example 1:
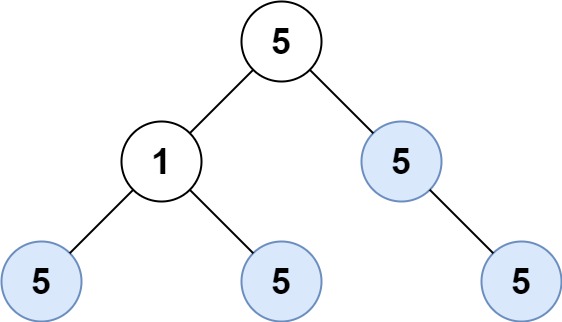
Input: root = [5,1,5,5,5,null,5] Output: 4
Example 2:
Input: root = [] Output: 0
Example 3:
Input: root = [5,5,5,5,5,null,5] Output: 6
Constraints:
- The number of the node in the tree will be in the range?
[0, 1000]. -1000 <= Node.val <= 1000
题目给定一棵二叉树,要求找出所有具有单一节点值的子树(即子树中所有节点值都相等),返回单一值子树的个数。
首先来看看对于一个节点,以该节点为根节点的子树在什么情况下是一棵单一值子树:
1)无左右子树,即叶节点,只有自己本身,那肯定是单一值子树。
2)只有左子树无右子树,那么左子树必须是单一值子树并且节点值必须等于其左子节点值;右子树为空无需判断(可以假定它就是单一值子树,直接返回True)。
3)只有右子树无左子树,那么右子树必须是单一值子树并且节点值必须等于其右子节点值;左子树为空无需判断(可以假定它就是单一值子树,直接返回True)。
4)具有左子树和右子树,那么左子树必须是单一值子树并且节点值必须等于左子节点值;并且右子树必须是单一值子树并且节点值必须等于其右子节点值。
根据以上分析,对于一个节点,首先需要知道其左右子树的情况,然后再判断该节点与其左右子节点是否相等,因此可以使用二叉树后序遍历算法(Postorder Traversal)进行遍历再按以上逻辑从底向上处理各个节点,统计单一值节点的个数。
class Solution:
def countUnivalSubtrees(self, root: Optional[TreeNode]) -> int:
self.res = 0
def helper(node):
if not node:
return True
left = helper(node.left)
right = helper(node.right)
if not left or not right:
return False
if (not node.left or node.left.val == node.val) and (not node.right or node.right.val == node.val):
self.res += 1
return True
return False
helper(root)
return self.res